🚩 알고리즘
- 문제를 이해할것
- 문제를 어떻게 해결할지 그림을 그리고, 수도코드를 짜고 시작
- 문제를 코드로 옮긴다.
코딩테스트 보면 한 3~4문제 주고
3시간~4시간 주어짐
문제를 받고 한문제당 한시간 할당한다 생각하고
3~40분 문제분석 / 20~30분 코드작성
프로그래머스 1~2단계(중소기업)
네카라쿠베 1문제정도는 3~4단계
🧩 시간복잡도
- big-O 표기법 : 최악의 경우를 고려, O(n) O(log n) 이런식으로 표기
- 시간걸리는순 : O(1)<O(log n)<O(n)<O(n^2)
🧩 공간복잡도
- 알고리즘이 수행되는데에 필요한 메모리의 총량
- 이것도 빅오표기법으로 표현함
- 시간복잡도보단 안중요.
🧩 그리디 알고리즘
- 무작정 눈앞에 보이는 최적의 상황만을 쫓아 해답에 도달하는 방법
- 선택절차 - 적절성검사 - 해답검사
🧩 알고리즘 구현의 기초
- 구현능력을 볼때 대표적으로 완전탐색과 시뮬레이션이 있다.
- 완전탐색 : 가능한 모든 경우의 수를 전부 확인하여 문제를 푸는 방식
- 시뮬레이션 : 문제에서 요구하는 복잡한 구현 요구사항을 하나도 빠뜨리지 않고 코드로 옮김
🧩 완전탐색
- 단순히 모든 경우의 수를 탐색하는 모든경우
- Brute Force(조건,반복으로 해결), 재귀, 순열, DFS/BFS
🧩 시뮬레이션
- 모든 과정과 조건이 제시되어, 그 과정을 거친 결과를 확인
- 해결법은 쉬우나 까다로워서 놓치기 쉬움
🧩 동적 계획법 (DP)
- 그리디와 다르게 모든 경우중 최적의 해법을 찾음
- 문제를 쪼개서 해결하고 결합하여 최종문제를 해결함
🧩 순열과 조합
- 순열 : nPr = n! / (n-r)!
ex) 사과, 오렌지, 레몬으로 이루어진 집합은 6개의 부분집합을 만들 수 있다. - 조합 : nCr = n! / r!(n-r)!
ex) 사과, 오렌지, 레몬으로 중복없이 만든다면 3개의 부분집합이 나올 수 있다.
🧩 GCD LCM
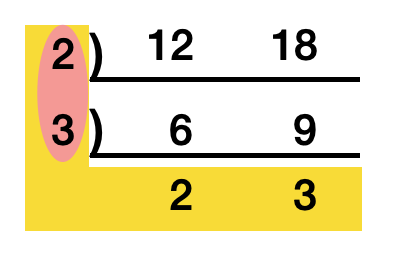
- GCD : 최대공약수, 두 수 이상의 여러 공약수중 최대인 수, 6과 9면 3
- LCM : 최소공배수, 두 수 이상의 여러 수중 공통된 배수, 12와 18이면 36
- 유클리드 호제법을 알면 GCD LCM 문제풀때 좋음
- 2개의 자연수 a, b가 있을 때 a를 b로 나눈 나머지가 r이라면
- a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 이론
- 유클리드 호제법에서 자연수 a와 b가 존재할 때, 해당 공식에 따라 계속해서 나누어 나가면 언젠가 나머지가 0인 상황이 도출되는데, 이때 나머지가 0이 되도록 나누는 수가 최대공약수이다
🧩 멱집합
- {1,2,3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 인데 이걸 통틀어 멱집합이라고 함
- 집합의 모든 부분집합
- 집합요소가 n개면 멱집합은 2^n개
