9주차 언어지능 딥러닝 (3)

정지원·2024년 4월 21일

에이블 스쿨 복습

목록 보기

38/51

딥러닝

딥러닝은 크게 3단계로 이루어짐

1단계 모델을 생성
2단계 학습
3단계 추론 및 테스트

과적합(Overfitting)

딥러닝에서 학습을 할 때 문제점은 OVERFITTING이다.

모델이 훈련 데이터에 너무 맞춰져서 학습된 패턴을 학습할 때 발생한다.
이는 모델이 훈련 데이터에는 잘 작동하지만 새로운 데이터에 대해서는 일반화(generalization)하지 못하는 현상이다.
과적합은 모델이 훈련 데이터에 포함된 잡음(noise까지 학습하여 훈련데이터에 대해 과도하게 적합하게 되는 경우에 발생한다.
과적합 방지 방법
- 더 많은 데이터수집
- 데이터 증강(Augmentation)
- 모델 복잡도 줄이기 (파라미터 수 제한 등)
- 규제(Rehularization) 가중치 규제
- 드롭아웃 (Dropout) 사용
- 교차 검증(Cross-validation)

CNN / RNN

CNN (Convolutional Neural Network)

주로 이미지 처리에 사용되는 딥러닝 모델
이미지의 특징을 추출하기 위해 Convolution과 pooling 레이어를 사용
Convolution layer는 이미지의 특징을 감지하고 추출하는 역할
pooling layer는 이미지의 크기를 줄이고 중요한 정보를 강조한다.
이를 통해 이미지의 특징 추출, 분류, 검출, 분할 등의 작업 수행

RNN (Recurrent Neural Network)

시계열 데이터나 자연어 같은 텍스트 데이터를 처리하는데 사용
반복되는 구조를 가지고 각 시간 단계에서 입력과 이전 시간 단계의 출력을 함께 고려하여 작동한다.
시간에 따른 패턴을 학습하고 이를 기반으로 다음 출력을 예측

=> 최근에는 CNN-RNN의 하이브리드 모델도 많이 사용되고 있다.

Linear Regression

$H(x) = Wx + b$
$H(x)$ : 가설(인공지능 모델)
$W$ : 기울기 (가중치)
$b$ : y 절편

원래 선형회귀분석에서는 직선의 방정식인 H(x)를 y(상수)와의 차이를 제곱하고 평균을 내주면 2차함수가 된다.
최적화가 가능해진다(즉, 그 코스트함수가 제일 작아지는 W 값을 구할 수 있음)
(H(x) - y) => 예측값 - 실제값 이다.
W가 최소가 되는게 좋음
이를 위해 경사하강법이 필요하다.

code

import torch
x_train = torch.FloatTensor([[1,2], [2,3], [3,4], [4,4], [5,3], [6,2]])
y_train = torch.FloatTensor([[0], [0], [0], [1], [1], [1]])
w = torch.randn([2,1], requires_grad=True)
b = torch.randn([1], requires_grad=True)
optimizer = torch.optim.SGD([w,b], lr=0.01)

# [딥러닝의 1단계]: 모델을 만든다.
def H(x) :
  return torch.sigmoid(torch.matmul(x, w) + b)  # H(x) = sigmoid(Wx + b)

# [딥러닝의 2단계] 학습을 한다
for stmp in range(2000):
  cost = -torch.mean(y_train * torch.log(H(x_train))+(1-y_train) * torch.log(1-H(x_train)))
  optimizer.zero_grad()
  cost.backward()
  optimizer.step()

# [딥러닝의 3단계] 추론/테스트를 한다.
x_test = torch.FloatTensor([[6,4]])
print(H(x_test))
print(H(x_test).detach())
print(H(x_test).detach().item())

경사 하강법

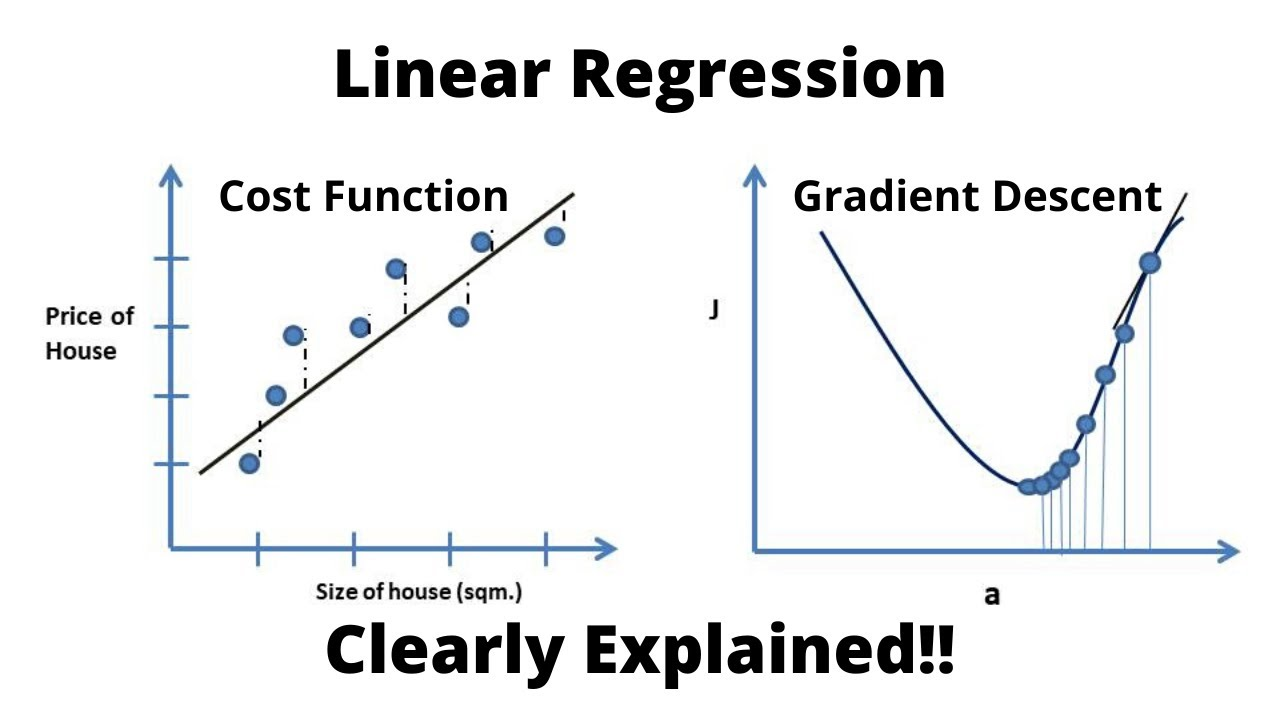
최적화에서 가장 일반적으로 사용되는 최적화 알고리즘 중 하나
주어진 cost함수 또는 손실함수의 값을 최소화 하기 위해 사용한다.
경사하강법 과정
- 초기화: 먼저 경사 하강법을 시작하기 전에 파라미터(가중치와 편향)를 임의의 값으로 초기화한다. (시작점 설정)
- 예측: 초기화된 파라미터를 사용하여 모델에 입력 데이터를 제공하고 예측값을 계산한다.
- 비용 계산: 예측값과 실제 타겟 값 사이의 차이를 계산하여 비용(손실)을 측정한다. 이 비용은 모델이 얼마나 잘 예측했는지를 나타냅니다. (MSE, 크로스 엔트로피 사용)
- 경사 계산: 비용 함수의 기울기(경사)를 계산한다. 이는 현재 파라미터 위치에서 비용 함수의 기울기를 나타내며, 이를 통해 우리는 비용을 줄이는 방향을 결정할 수 있다.
- 파라미터 업데이트: 경사의 반대 방향으로 일정한 거리(학습률)만큼 이동하여 새로운 파라미터를 업데이트한다. 이는 현재 위치에서 비용 함수를 최소화하는 방향으로 파라미터를 업데이트하는 과정입니다
- 종료 조건 확인: 미리 정해진 종료 조건을 확인하고, 만족할 때까지 2번부터 5번의 과정을 반복한다. 종료 조건은 주로 특정 반복 횟수에 도달하거나 비용 함수의 변화가 미미할 때 종료하는 등의 방식으로 설정됩니다.
- 학습 종료: 종료 조건을 만족하면 경사 하강법의 학습이 종료한다. 이 때의 파라미터는 비용 함수를 최소화하는 값으로 수렴함

Binary Classification

이진 분류의 예시

이메일 스팸 구분
페이스북 피드 추천
신용카드 사용 패턴 본인 여부 분류

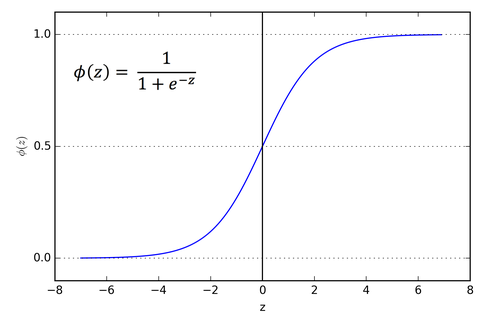
Linear regression의 $H(x) = Wx + b$ 이를 사용하고
조건을 추가하여 Logistic / sigmoid function 사용함
$H(x)$ 에 시그모이드를 적용하면 2차함수가 아닌 아래와 같은 울퉁불퉁한 모양의 함수가 나온다.
그래서 코스트 함수가 가장 작아지는 W를 찾는게 불가능하다. => log적용

이진분류의 문제점

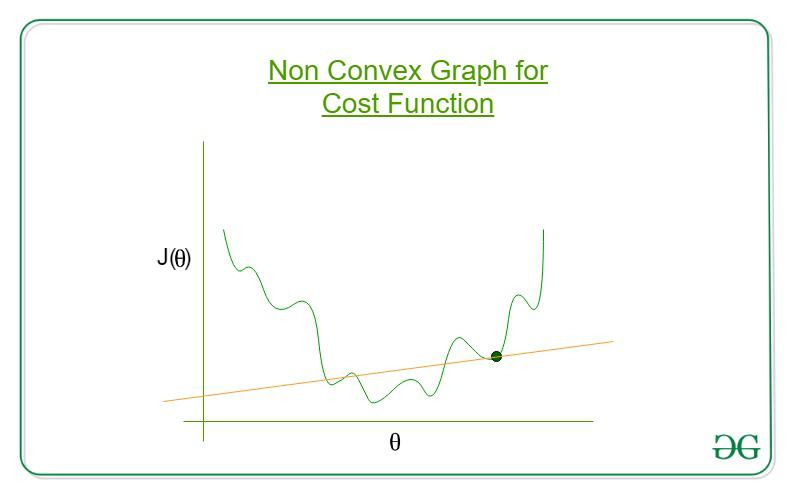
코스트함수가 위처럼 울퉁불퉁하게 생겼다면 제일 작은 값을 찾아기 힘들다.
그림에 있는 점으로 수렴할 수 있기 때문이다.
그래서 linear regression에서 사용했던 cost 함수를 사용하기 어렵다.
이 문제를 해결하기 위해 log를 사용하여 cost 함수를 생성한다.

$\text{Cost}(W) = -\frac{1}{m}\sum_{i=1}^{m} \left( y_i \log(H(x_i)) + (1 - y_i) \log(1 - H(x_i)) \right)$

code

import torch
x_train = torch.FloatTensor([[1,2], [2,3], [3,4], [4,4], [5,3], [6,2]])
y_train = torch.FloatTensor([[0], [0], [0], [1], [1], [1]])
w = torch.randn([2,1], requires_grad=True)
b = torch.randn([1], requires_grad=True)
optimizer = torch.optim.SGD([w,b], lr=0.01)

# [딥러닝의 1단계]: 모델을 만든다.
def H(x) :
  return torch.sigmoid(torch.matmul(x, w) + b)  # H(x) = sigmoid(Wx + b)

# [딥러닝의 2단계] 학습을 한다
for stmp in range(2000):
  cost = -torch.mean(y_train * torch.log(H(x_train))+(1-y_train) * torch.log(1-H(x_train)))
  optimizer.zero_grad()
  cost.backward()
  optimizer.step()

# [딥러닝의 3단계] 추론/테스트를 한다.
print(H(x_train))

print('==========================')
#============================================================================
# 비선형 테스트
#============================================================================
x_train = torch.FloatTensor([[1,2], [2,3], [3,4], [4,4], [5,3], [6,2], [6,4]])
y_train = torch.FloatTensor([[0], [0], [0], [1], [1], [1], [0]])

print(H(x_train))
        # [[0.1257], 0
        # [0.1675],  0
        # [0.2197],  0
        # [0.6605],  1
        # [0.9852],  1
        # [0.9996],  1
        # [0.9893]]  0

Softmax Classificaton

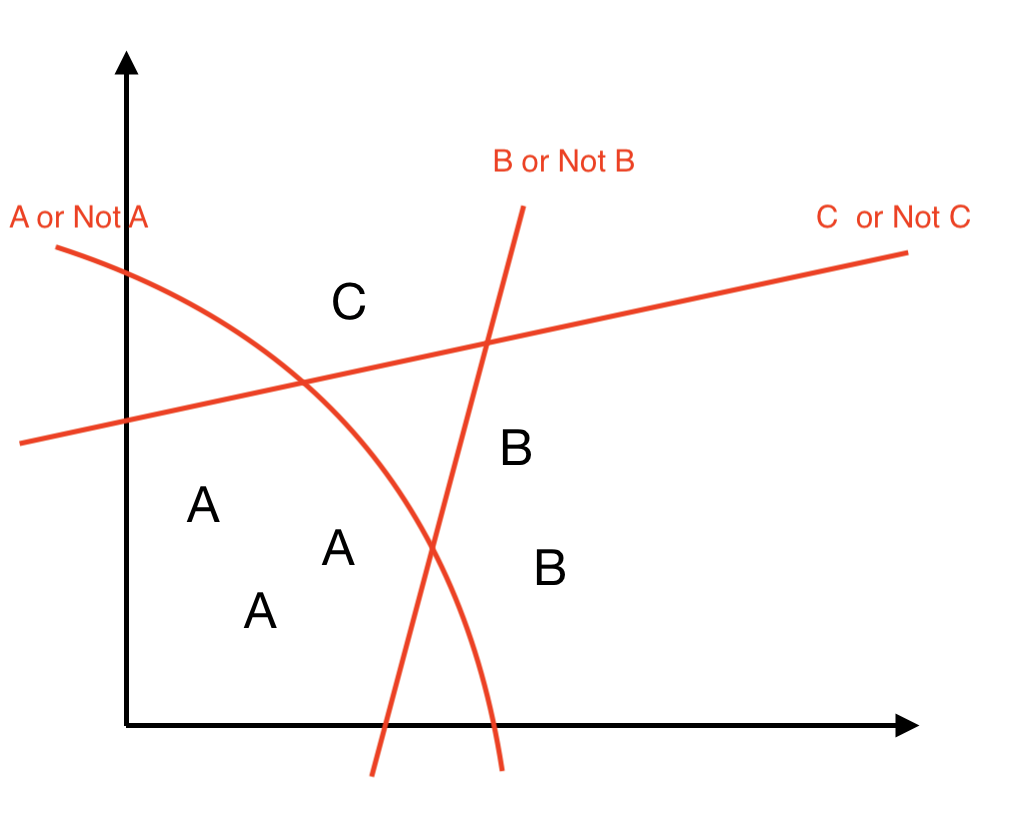
보통 세가지를 분류하려면 "A, B, C 중 어떤 건가요?" 의 질문에
예/아니오 로 답을 할 수 없다.
이를 각각 sigmoid를 적용하여 나타낼 수 있음
우리가 알고 있는 이진분류기는 예/ 아니오로 대답할 수 있다.
이를 softmax를 적용하려면

Q1) A인가 아닌가?
A1) 예 (이진분류에서 0.5보다 큰 값이 나옴) 0.99999

Q2) B인가 아닌가?
A2) 예 (이진분류에서 0.5보다 큰 값이 나옴) 0.50001

Q3) C인가 아닌가?
A3) 아니오

=> A가 이 질문에 대한 가장 가까운 정답이다.