Section 3 - 50일차

1. Toy - 23일차

• 배열을 나선형으로 조회하는 문제
• isVisit?과 조건문등을 통해서 해결하였음

2. 자료구조 / 알고리즘

• 알고리즘이란? 문제를 어떤 식으로 푸는 것이 최선인가?

• 시간복잡도
  입력값의 증가/감소에 따라 작업시간이 얼마만큼 비례하여 증가/감소하는가?
  효율적인 알고리즘? 입력값이 증가함에 따라 증가되는 작업시간이 최소화된 알고리즘

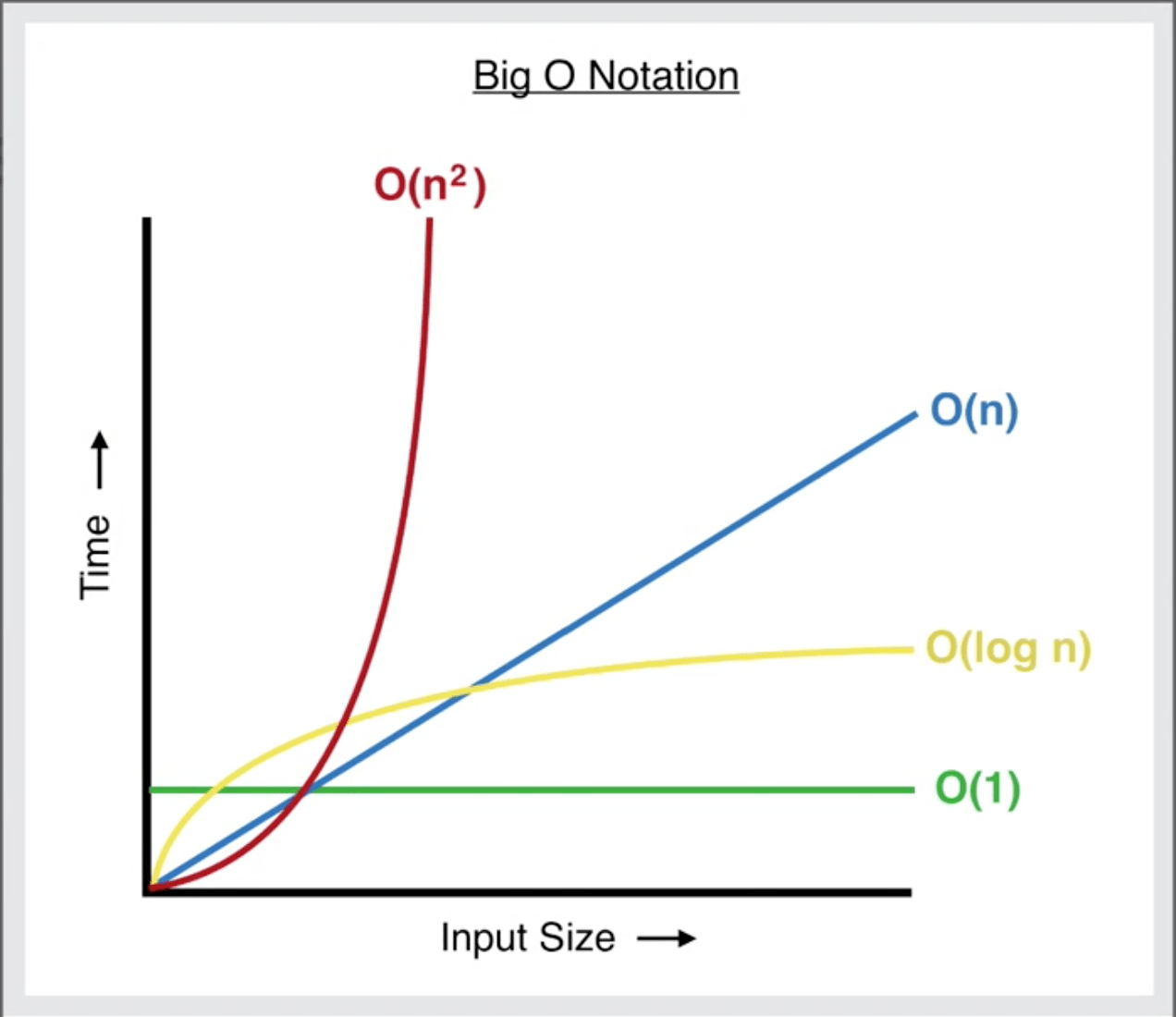
• 시간 복잡도 표기
  Big-O - 최악 >> 흔히 사용됨, 최대 이 정도까지 시간이 걸릴 수 있다!!
  Big-Ω - 최선
  Big-θ - 중간(평균)
  

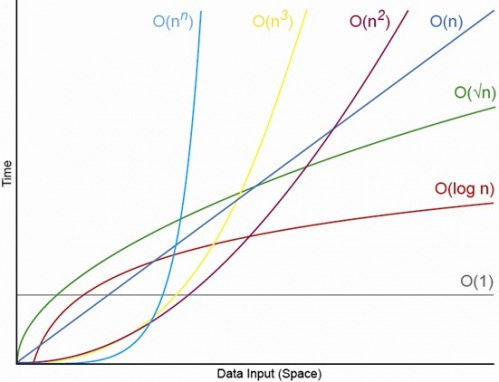
• O(1)
  입력값에 따라 시간의 변화가 없음, 입력값에 관계없이 출력값을 얻어낼 수 있는 경우
  ex)

function ex(arr, index){
	return arr[index];
}

• O(n)
  linear, 입력값의 증가와 시간의 증가가 같은 비율로 증가하는 것
  ex)

function ex(n){
	for(let i = 0 ; i < n ; i++){
    	// do something
    }
}

O(n), O(2n), O(3n) ... 계속 증가한다면 n앞의 계수의 의미가 없어지므로 O(n)으로 표기

• O(n^2)
  입력값의 증가에 따라 시간이 제곱에 비례하여 증가하는 것
  입력값 1 => 1초
  입력값 5 => 25초
  ex) 중첩 반복문

• O(2^n)
  시간이 2배씩 늘어남
  ex)

function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}

• Greedy Algorithm 탐욕 알고리즘
  당장 눈앞에 보이는 최적의 상황만을 쫓아 해답에 도달하는 방법
  절차

  선택 절차(Selection Procedure) 현재 상태에서의 최적의 해답 선택
  적절성 검사(Feasibility Check) 선택된 해가 조건에 맞는지 검사
  해답 검사(Solution Check) 문제가 해결되었는지 검사, 해결되지 않았다면 1번으로 돌아가 반복

최소비용 신장 트리 : 그래프 내의 모든 정점을 최소 비용으로 연결하는 트리
Kruskal 알고리즘 : 최소비용 신장 트리를 만드는 알고리즘 중 탐욕 알고리즘을 이용한 풀이

항상 최적의 결과를 보장하지는 못한다
=> 2가지 조건을 만족할 때, 잘 작동함

탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다
최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성

항상 최적은 아니지만, 어느 정도 최적해에 근사한 값을 빠르게 도출할 수 있다. 근사 알고리즘으로 사용 가능

• Dynamic Programming 동적 프로그래밍
  주어진 문제를 여러 하위 문제로 나누어 풀고, 하위 문제들의 방법을 결합하여 최종 문제를 해결하는 방식
  두가지 조건

  • 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제들은 중복된다 (Overlapping Sub-problems)
  • 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다.

Bottom-up => 작은 문제에서부터 시작하여 큰 문제를 해결해 나가는 방법, 반복문
Top-down => 큰 문제에서 작은 문제로 내려가는 것 처럼, 큰 문제를 위해 작은 문제를 호출, 재귀

3. review

• DFS 재귀 활용, BFS queue 활용