알고리즘 공부

[프로그래머스] 정수 삼각형

---

문제 설명

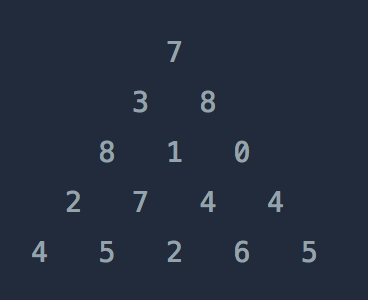
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

제한사항

• 삼각형의 높이는 1 이상 500 이하입니다.
• 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

입출력 예

triangle: 
	[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
result: 
	30

---

풀이

처음에는 단순히 아래 칸에서 큰 값을 더하는 방식을 생각했으나, 이 경우 예제를 계산했을 때 7+8+1+7+5 = 28로 적절하지 못한 해결 방안이었다.
따라서 아래 칸에서 부터 계산해서 올라가는 방법을 사용해서 풀었다. (완전 탐색의 경우, 높이가 최대 500까지라 시간 복잡도가 너무 커질 것이라 판단해서 제외)

예제에서 맨 아래 칸에서 바로 윗 칸으로 덧셈을 해서 더 큰 값을 선택하게 되면,
첫 단계: [4,5,2,6,5]와 [2,7,4,4,]를 계산 -> [7,12,10,10]
전체 배열 = [[7], [3,8], [8,1,0], [7,12,10,10], [4,5,2,6,5]]

두번째 단계: [8,1,0]와 [7,12,10,10] 계산 -> [20,13,10]
전체 배열 = [[7], [3,8], [20,13,10], [7,12,10,10], [4,5,2,6,5]]

세번째 단계: [3,8]와 [20,13,10] 계산 -> [23,21]
전체 배열 = [[7],[23,21], [20,13,10], [7,12,10,10], [4,5,2,6,5]]

네번째 단계: [7]와 [23,21] 계산 -> [30]
전체 배열 = [[30],[23,21], [20,13,10], [7,12,10,10], [4,5,2,6,5]]

전체 진행 후 꼭대기 숫자의 값 = 최대 값이 된다.

코드

def solution(triangle):
	# 배열의 마지막에서 두번째 줄[n-2]부터 역순으로 계산 시작
    for row in range(len(triangle) - 2, -1, -1):
        for col in range(len(triangle[row])):
            # 아래 줄에서 큰 값을 더해서 배열에 저장
            triangle[row][col] += max(triangle[row+1][col], triangle[row+1][col+1])
    # 꼭대기 숫자가 최대값이 된다
    return triangle[0][0]

결과

통과

---

다른 사람의 풀이

통과 후 다른 사람의 풀이를 봤는데 신기한 풀이가 있었다.

solution = lambda t, l = []: max(l) if not t else solution(t[1:], [max(x,y)+z for x,y,z in zip([0]+l, l+[0], t[0])])

lambda t, l=\[] : t에 삼각형 배열 저장, l은 각 단계에서 계산된 결과 저장. l의 기본 값은 []
max(l) if not t else ...: t가 비어있는 경우 max(l) 반환, 아닌 경우 ... 부분 실행
solution(t[1:], [max(x,y)+z for x,y,z in zip([0]+l, l+[0], t[0])]): 재귀적 solution 함수 호출. t[1:]은 첫번째 행을 제외한 나머지 배열을 의미.

재귀 호출로 DP 상향식 계산을 구현한거 같은데 아직 완벽히 이해는 안된다. 매우 신기한 풀이인듯