문제 설명
개발자를 희망하는 죠르디가 카카오에 면접을 보러 왔습니다.
코로나 바이러스 감염 예방을 위해 응시자들은 거리를 둬서 대기를 해야하는데 개발 직군 면접인 만큼
아래와 같은 규칙으로 대기실에 거리를 두고 앉도록 안내하고 있습니다.
- 대기실은 5개이며, 각 대기실은 5x5 크기입니다.
- 거리두기를 위하여 응시자들 끼리는 맨해튼 거리1가 2 이하로 앉지 말아 주세요.
- 단 응시자가 앉아있는 자리 사이가 파티션으로 막혀 있을 경우에는 허용합니다.
예를 들어,
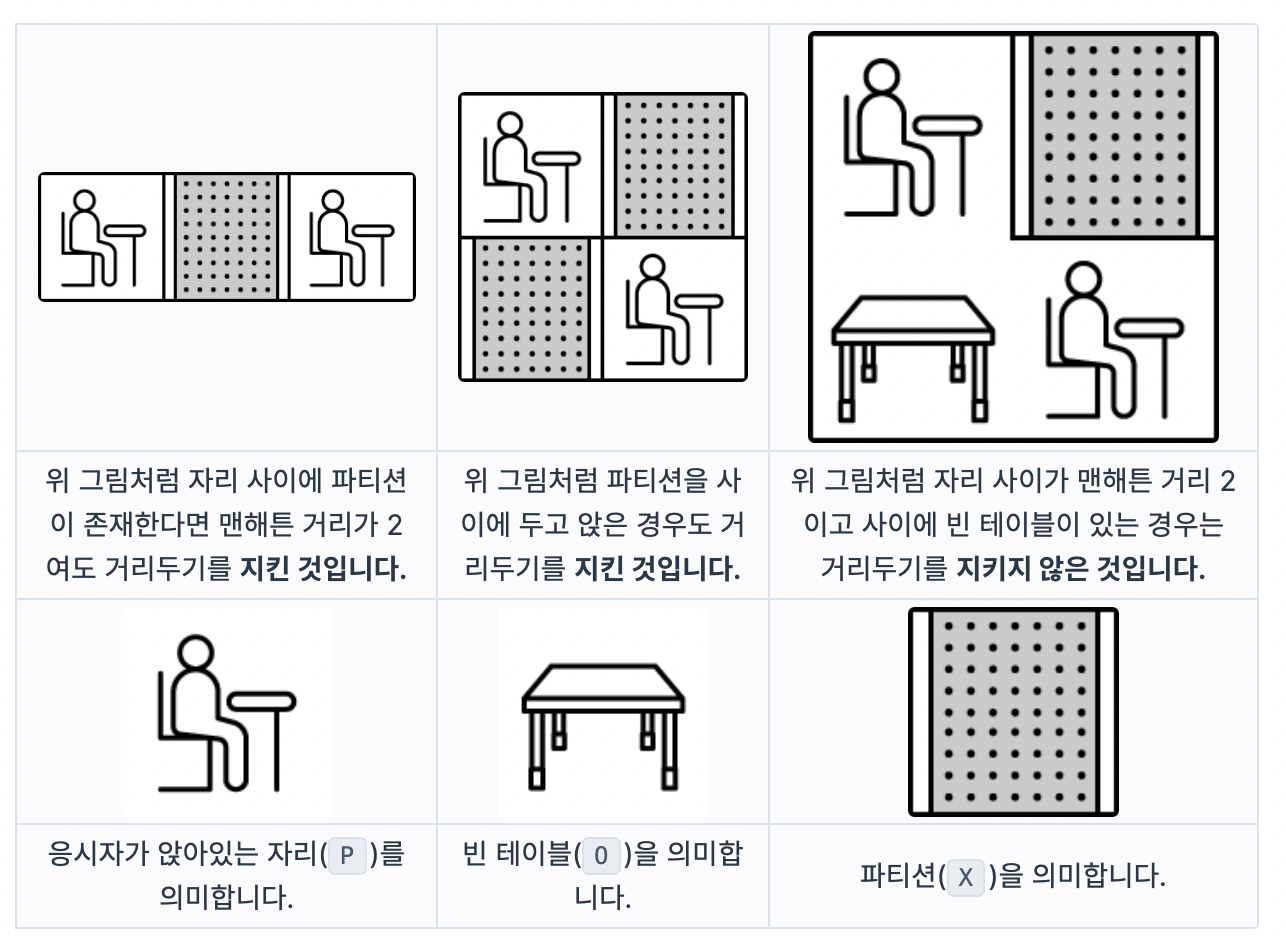
5개의 대기실을 본 죠르디는 각 대기실에서 응시자들이 거리두기를 잘 기키고 있는지 알고 싶어졌습니다. 자리에 앉아있는 응시자들의 정보와 대기실 구조를 대기실별로 담은 2차원 문자열 배열 places가 매개변수로 주어집니다. 각 대기실별로 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- places의 행 길이(대기실 개수) = 5
- places의 각 행은 하나의 대기실 구조를 나타냅니다. - places의 열 길이(대기실 세로 길이) = 5
- places의 원소는 P,O,X로 이루어진 문자열입니다.
- places 원소의 길이(대기실 가로 길이) = 5
- P는 응시자가 앉아있는 자리를 의미합니다.
- O는 빈 테이블을 의미합니다.
- X는 파티션을 의미합니다. - 입력으로 주어지는 5개 대기실의 크기는 모두 5x5 입니다.
- return 값 형식
- 1차원 정수 배열에 5개의 원소를 담아서 return 합니다.
- places에 담겨 있는 5개 대기실의 순서대로, 거리두기 준수 여부를 차례대로 배열에 담습니다.
- 각 대기실 별로 모든 응시자가 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 담습니다.
입출력 예
| places | result |
|---|---|
| [["POOOP", "OXXOX", "OPXPX", "OOXOX", "POXXP"], ["POOPX", "OXPXP", "PXXXO", "OXXXO", "OOOPP"], ["PXOPX", "OXOXP", "OXPOX", "OXXOP", "PXPOX"], ["OOOXX", "XOOOX", "OOOXX", "OXOOX", "OOOOO"], ["PXPXP", "XPXPX", "PXPXP", "XPXPX", "PXPXP"]] | [1, 0, 1, 1, 1] |
입출력 예 설명
입출력 예 #1
첫 번째 대기실
| No. | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | P | O | O | O | P |
| 1 | O | X | X | O | X |
| 2 | O | P | X | P | X |
| 3 | O | O | X | O | X |
| 4 | P | O | X | X | P |
- 모든 응시자가 거리두기를 지키고 있습니다.
두 번째 대기실
| No. | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | P | O | O | P | X |
| 1 | O | X | P | X | P |
| 2 | P | X | X | X | O |
| 3 | O | X | X | X | O |
| 4 | O | O | O | P | P |
- (0, 0) 자리의 응시자와 (2, 0) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
- (1, 2) 자리의 응시자와 (0, 3) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
- (4, 3) 자리의 응시자와 (4, 4) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
세 번째 대기실
| No. | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | P | X | O | P | X |
| 1 | O | X | O | X | P |
| 2 | O | X | P | O | X |
| 3 | O | X | X | O | P |
| 4 | P | X | P | O | X |
- 모든 응시자가 거리두기를 지키고 있습니다.
네 번째 대기실
| No. | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | O | O | O | X | X |
| 1 | X | O | O | O | X |
| 2 | O | O | O | X | X |
| 3 | O | X | O | O | X |
| 4 | O | O | O | O | O |
- 대기실에 응시자가 없으므로 거리두기를 지키고 있습니다.
다섯 번째 대기실
| No. | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | P | X | P | X | P |
| 1 | X | P | X | P | X |
| 2 | P | X | P | X | P |
| 3 | X | P | X | P | X |
| 4 | P | X | P | X | P |
- 모든 응시자가 거리두기를 지키고 있습니다.
두 번째 대기실을 제외한 모든 대기실에서 거리두기가 지켜지고 있으므로, 배열 [1, 0, 1, 1, 1]을 return 합니다.
문제 풀이
from collections import deque
def func(seat,r,c):
queue=deque([(r,c,0)])
visited=[]
vec=[[0,1],[1,0],[0,-1],[-1,0]]
while queue:
r,c,d=queue.popleft()
visited.append((r,c))
for v in vec:
xr=r+v[0]
yc=c+v[1]
dis=d+1
if 0<=xr<5 and 0<=yc<5 and (xr,yc) not in visited:
visited.append((xr,yc))
if seat[xr][yc]=='P':
if dis<3:
return 0
elif seat[xr][yc]=='O':
if dis==1:
#처음 P 발견한 구간에서 dis 거리만큼 떨어져 있음
#dis만큼 떨어진 곳에서 다시 bfs 탐색
queue.append((xr,yc,dis))
return 1
def solution(places):
answer = []
for place in places:
ans=1
for i in range(5):
for j in range(5):
if place[i][j]=='P':
result=func(place,i,j)
if result==0:
ans=0
answer.append(ans)
return answer- 결국 다른 사람 풀이를 참고했다.
- BFS를 이용하여 문제를 푸는 것이 이해가 안가서 그대로 따라가다보니 결국 모두 참고하게 되었음
- 대기실에 P가 발견되면 응시자의 맨해튼 거리 내에서 BFS 수행 → 거리두기 지켜지고 있는지 확인
- 최종 반환값이 1이면 거리두기를 잘 하고 있는 것, 중간에 0이 반환되면 거리두기를 지키지 않은 것.
다른 사람 풀이
def solution(places):
result = []
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def f(i, j, cnt):
nonlocal good
if cnt >2 : return
if -1<i<5 and -1<j<5:
if graph[i][j] == 'X':
return
if cnt != 0 and graph[i][j] == 'P':
good = 0
return
graph[i][j] = 'X'
for w in range(4):
ni = i+dx[w]
nj = j+dy[w]
f(ni, nj, cnt+1)
for case in places:
graph = [list(r) for r in case]
good = 1
for i in range(5):
for j in range(5):
if graph[i][j]=='P':
f(i,j,0)
result.append(good)
return result