넴모넴모(Easy)

문제

네모는 뿌××× 게임에 깊은 감명을 받아, 직사각형 모양의 격자판과 “넴모”라는 수수께끼의 생물을 이용하는 “넴모넴모”라는 게임을 만들었다. 이 게임의 규칙은 아주 간단하다. 격자판의 비어 있는 칸을 임의로 골라 “넴모”를 하나 올려놓거나, “넴모”가 올라간 칸 네 개가 2 × 2 사각형을 이루는 부분을 찾아 그 위에 있는 “넴모”들을 모두 없애는 것을 질릴 때까지 반복하면 된다.

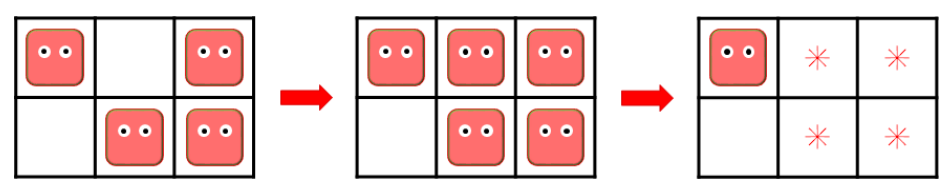
하지만 안타깝게도 게임은 정말 재미가 없었고, 네모는 아주 빨리 질려 버리고 말았다. 실망한 네모는 게임을 적당히 플레이하다가, “넴모”를 없애고 싶은데 격자판 위에 없앨 수 있는 “넴모”가 없으면 게임을 그만두기로 했다. 네모가 게임을 그만두었을 때 나올 수 있는 “넴모”의 배치의 가짓수를 구하여라.

입력

첫 번째 줄에 격자판의 행의 개수 N, 열의 개수 M(1 ≤ N, M ≤ 25, 1 ≤ N × M ≤ 25)이 공백으로 구분되어 주어진다.

출력

첫 번째 줄에 주어진 격자판에서 나올 수 있는, “넴모”들이 올라간 칸이 2 × 2 사각형을 이루지 않는 모든 배치의 가짓수를 출력한다.

예제 입력 1

2 2

예제 출력 1

15

예제 입력 2

2 3

예제 출력 2

57

예제 입력 3

3 5

예제 출력 3

22077

문제 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class BJ14712 {
    static boolean[] visited;
    static int count;
    static int N,M;
    public static void main(String[] args) throws IOException {
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st=new StringTokenizer(br.readLine());

        N=Integer.parseInt(st.nextToken());
        M=Integer.parseInt(st.nextToken());

        //넴모의 개수
        visited=new boolean[N*M];

        subset(0,N*M);

        System.out.print(count);
    }

    private static void subset(int index,int R){
        if(index==R){
            //2x2가 아니라면 count++
            for (int i = 0; i < N * M; i++) {
                if (visited[i] && i % M != M - 1 && i+M+1<N*M) {
                    if (visited[i + 1] && visited[i + M] && visited[i + M + 1]) {
                        return;
                    }
                }
            }
            count++;
            return;
        }

        visited[index]=true;
        subset(index+1,R);

        visited[index]=false;
        subset(index+1,R);
    }
}

N x M 격자크기에서 2X2의 넴모가 합쳐지지 않은 경우의 개수를 모두 구하면 되는 문제이다.

우선 넴모의 개수가 1개일수도, 2개일수도 혹은 N x M 개 일 수도 있는데 모든 경우를 구해야한다. 이 구간에서 감을 잡을 수 있는데 부분집합을 이용하여 문제를 해결할 수 있다.

N행 M열의 배열을 만들어 부분집합을 구하는 것보다 1차원 배열을 만들어 부분집합을 구하고 인덱스를 이용하여 행과 열을 구하여 2X2 넴모의 경우를 구하는 방식을 사용했다.

부분집합을 통한 넴모 배치하기

private static void subset(int index,int R){
    if(index==R){
        //2x2가 아니라면 count++
        for (int i = 0; i < N * M; i++) {
            if (visited[i] && i % M != M - 1 && i+M+1<N*M) {
                if (visited[i + 1] && visited[i + M] && visited[i + M + 1]) {
                    return;
                }
            }
        }
        count++;
        return;
    }

    visited[index]=true;
    subset(index+1,R);

    visited[index]=false;
    subset(index+1,R);
}

부분집합을 구하는 기본 로직을 구현하고 index가 N x M이 되었다면 2X2의 넴모가 있는지 확인해야한다.

• 해당 위치에 넴모가 있는지 확인하고
• 인덱스 % 열의 개수로 나눈 나머지 == 2차원 배열로 만들었을때의 열이 열의 마지막이 아닌 경우 체크

i번째 인덱스, i+1번째, i+M번째, i+M+1번째 인덱스의 값들이 모두 넴모가 있다면 2X2의 조건을 만족했기 때문에 정답으로 구해야하는 경우의 수에는 포함되지 않아 return 해주고

2X2 조건을 만족하지 않는다면 경우의 수를 증가시켜준다.

//넴모의 개수
visited=new boolean[N*M];

subset(0,N*M);

System.out.print(count);

위의 로직을 모두 만족하면 금방 답을 구할 수 있다.