다리 놓기

조소복·2022년 8월 10일

문제

재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)

재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

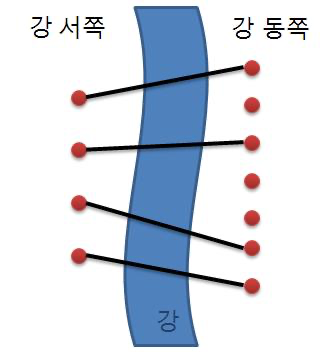
입력

입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.

출력

각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.

예제 입력 1

예제 출력 1

1
5
67863915

문제 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.math.BigInteger;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
	static BigInteger count;
	static int M;
	static int N;
	static BigInteger[] fac=new BigInteger[31];

	public static void main(String[] args) throws IOException {
		BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st=new StringTokenizer(br.readLine());
		StringBuilder sb=new StringBuilder();
		fac[0]=new BigInteger(""+1);
		
		for(int i=1;i<31;i++) {
			Integer num=i;
			BigInteger big=new BigInteger(""+num);
			fac[i]=big.multiply(fac[i-1]);
		}
		
		int T=Integer.parseInt(st.nextToken());
		for(int t=0;t<T;t++) {
			st=new StringTokenizer(br.readLine());
			N=Integer.parseInt(st.nextToken());
			M=Integer.parseInt(st.nextToken());
			
			count=fac[M].divide(fac[M-N].multiply(fac[N]));
			
			sb.append(count+"\n");
		}
		System.out.println(sb);
	}
	
}