멀쩡한 사각형

문제 설명

가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

제한사항

• W, H : 1억 이하의 자연수

입출력 예

W	H	result
8	12	80

입출력 예 설명

입출력 예 #1

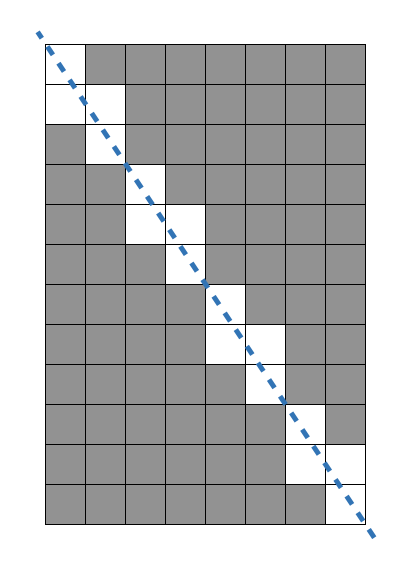
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

문제 풀이

• 완벽한 수리문제 (도저히 모르겠어서 찾아봤음..)
• 두 변 길이의 합에서 최대공약수를 빼면 사용할 수 없는 사각형의 개수가 나옴

from math import gcd
def solution(w,h):
    answer = 1
    
    return w*h-(w+h-gcd(w,h))

풀어서 짜본 최대공약수 코드

def solution(w,h):
    gcd=1
    for i in range(min(w,h)+1,0,-1):
        if w%i==0 and h%i==0:
            gcd=i
            break
            
    return w*h-(w+h-gcd)

유클리드 호제법

def gcd(a,b): return b if (a==0) else gcd(b%a,a)

JavaScript에서 기울기 이용한 사용 불가능한 사각형 구하는 방법이 있었음