오목

문제

오목은 바둑판에 검은 바둑알과 흰 바둑알을 교대로 놓아서 겨루는 게임이다. 바둑판에는 19개의 가로줄과 19개의 세로줄이 그려져 있는데 가로줄은 위에서부터 아래로 1번, 2번, ... ,19번의 번호가 붙고 세로줄은 왼쪽에서부터 오른쪽으로 1번, 2번, ... 19번의 번호가 붙는다.

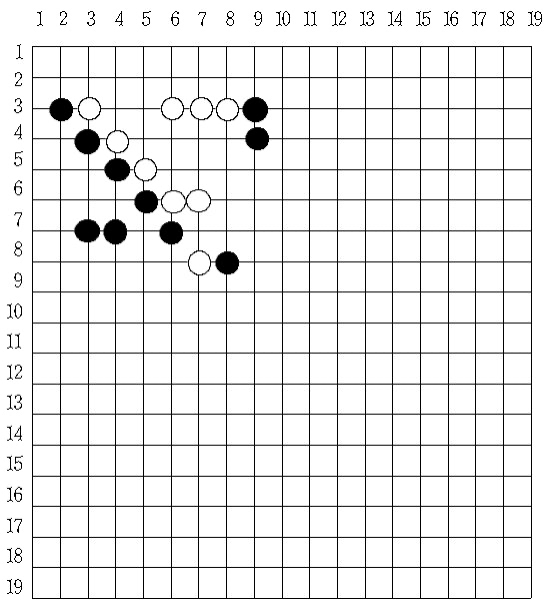
위의 그림에서와 같이 같은 색의 바둑알이 연속적으로 다섯 알을 놓이면 그 색이 이기게 된다. 여기서 연속적이란 가로, 세로 또는 대각선 방향 모두를 뜻한다. 즉, 위의 그림은 검은색이 이긴 경우이다. 하지만 여섯 알 이상이 연속적으로 놓인 경우에는 이긴 것이 아니다.

입력으로 바둑판의 어떤 상태가 주어졌을 때, 검은색이 이겼는지, 흰색이 이겼는지 또는 아직 승부가 결정되지 않았는지를 판단하는 프로그램을 작성하시오. 단, 검은색과 흰색이 동시에 이기거나 검은색 또는 흰색이 두 군데 이상에서 동시에 이기는 경우는 입력으로 들어오지 않는다.

입력

19줄에 각 줄마다 19개의 숫자로 표현되는데, 검은 바둑알은 1, 흰 바둑알은 2, 알이 놓이지 않는 자리는 0으로 표시되며, 숫자는 한 칸씩 띄어서 표시된다.

출력

첫줄에 검은색이 이겼을 경우에는 1을, 흰색이 이겼을 경우에는 2를, 아직 승부가 결정되지 않았을 경우에는 0을 출력한다. 검은색 또는 흰색이 이겼을 경우에는 둘째 줄에 연속된 다섯 개의 바둑알 중에서 가장 왼쪽에 있는 바둑알(연속된 다섯 개의 바둑알이 세로로 놓인 경우, 그 중 가장 위에 있는 것)의 가로줄 번호와, 세로줄 번호를 순서대로 출력한다.

예제 입력 1

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 2 0 0 2 2 2 1 0 0 0 0 0 0 0 0 0 0
0 0 1 2 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

예제 출력 1

1
3 2

문제 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static int[][] result=new int[5][2];

    public static void main(String[] args) throws IOException {
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        int[][] board=new int[19][19];
        int a=-1;
        int b=-1;

        for(int i=0;i<19;i++){
            st=new StringTokenizer(br.readLine());
            for(int j=0;j<19;j++){
                board[i][j]=Integer.parseInt(st.nextToken());
            }
        }

        for(int i=0;i<19;i++){
            for(int j=0;j<19;j++){
                //오목 확인
                //오른쪽, 오른쪽 아래 대각선, 아래, 왼쪽 아래 대각선
                if(board[i][j]==0) continue;

                if(j+1<19 && board[i][j+1]==board[i][j]){
                    if(omok(board,i,j,0)){
                        a=i;
                        b=j;
                        break;
                    }
                }
                if(i+1<19 && j+1<19 && board[i+1][j+1]==board[i][j]){
                    if(omok(board,i,j,1)){
                        a=i;
                        b=j;
                        break;
                    }
                }
                if(i+1<19 && board[i+1][j]==board[i][j]){
                    if(omok(board,i,j,2)){
                        a=i;
                        b=j;
                        break;
                    }
                }
                if(i+1<19 && j-1>=0 && board[i+1][j-1]==board[i][j]){
                    if(omok(board,i,j,3)){
                        a=i;
                        b=j;
                        break;
                    }
                }
            }

            if(a!=-1 && b!=-1) break;
        }

        if(a==-1 && b==-1){
            System.out.println(0);
        }else {
            System.out.println(board[a][b]);

            //왼쪽, 상위
            if(result[0][0]+1==result[1][0] && result[0][1]==result[1][1]){
                System.out.println((result[0][0]+1)+" "+(result[0][1]+1));
            }else{
                int idx=0;

                for(int i=0;i<5;i++){
                    if(result[i][1]<result[idx][1]) idx=i;
                }

                System.out.print((result[idx][0]+1)+" "+(result[idx][1]+1));
            }

        }

    }

    //오른쪽, 오른쪽 아래 대각선, 아래, 왼쪽 아래 대각선
    private static boolean omok(int[][] board,int i,int j,int dir) {
        int cnt=0;
        int tmp_dir=dir;

        if(dir==0){
            for(int n=0;n<6;n++){
                if(j+n>=19) break;
                if(board[i][j+n]!=board[i][j]) break;
                cnt++;

                if(n==5) break;
                result[n][0]=i;
                result[n][1]=j+n;
            }
        }else if(dir==1){
            for(int n=0;n<6;n++){
                if(i+n>=19 || j+n>=19) break;
                if(board[i+n][j+n]!=board[i][j]) break;
                cnt++;

                if(n==5) break;
                result[n][0]=i+n;
                result[n][1]=j+n;
            }
        }else if(dir==2){
            for(int n=0;n<6;n++){
                if(i+n>=19) break;
                if(board[i+n][j]!=board[i][j]) break;
                cnt++;

                if(n==5) break;
                result[n][0]=i+n;
                result[n][1]=j;
            }
        }else if(dir==3){
            for(int n=0;n<6;n++){
                if(i+n>=19 || j-n<0) break;
                if(board[i+n][j-n]!=board[i][j]) break;
                cnt++;

                if(n==5) break;
                result[n][0]=i+n;
                result[n][1]=j-n;
            }
        }

        if(cnt==5) {
            if(tmp_dir==0){
                if(j-1>=0 && board[i][j-1]==board[i][j]) {
                    result=new int[5][2];
                    return false;
                }
            }else if (tmp_dir==1){
                if(i-1>=0 && j-1>=0 && board[i-1][j-1]==board[i][j]) {
                    result=new int[5][2];
                    return false;
                }
            }else if(tmp_dir==2){
                if(i-1>=0 && board[i-1][j]==board[i][j]) {
                    result=new int[5][2];
                    return false;
                }
            }else if(tmp_dir==3){
                if(i-1>=0 && j+1<19 && board[i-1][j+1]==board[i][j]) {
                    result=new int[5][2];
                    return false;
                }
            }
            return true;
        }

        result=new int[5][2];
        return false;
    }
}

문제를 풀기 위해서는 두 가지의 로직이 필요하다.

1. 오목 찾기
2. 오목 중 상위 혹은 왼쪽의 값 좌표 찾기

오목 찾기

우선 오목을 찾기 위해서는 9방향을 모두 탐색할 수도 있겠지만 반복문을 차례대로 돌리기 때문에 오른쪽, 오른쪽 아래 대각선, 아래, 왼쪽 아래 대각선 방향으로 오목을 찾으면 된다.

이때, 유의해야할 점은 5개의 바둑돌이 있어야하지 6개 이상이 있어선 안된다는 점이다.

Main 함수

for(int i=0;i<19;i++){
    for(int j=0;j<19;j++){
        //오목 확인
        //오른쪽, 오른쪽 아래 대각선, 아래, 왼쪽 아래 대각선
        if(board[i][j]==0) continue;
    
        if(j+1<19 && board[i][j+1]==board[i][j]){
            if(omok(board,i,j,0)){
                a=i;
                b=j;
                break;
            }
        }
        if(i+1<19 && j+1<19 && board[i+1][j+1]==board[i][j]){
            if(omok(board,i,j,1)){
                a=i;
                b=j;
                break;
            }
        }
        if(i+1<19 && board[i+1][j]==board[i][j]){
            if(omok(board,i,j,2)){
                a=i;
                b=j;
                break;
            }
        }
        if(i+1<19 && j-1>=0 && board[i+1][j-1]==board[i][j]){
            if(omok(board,i,j,3)){
                a=i;
                b=j;
                break;
            }
        }
    }

    if(a!=-1 && b!=-1) break;
}

우선 완전탐색을 통해 바둑돌이 놓여져있는 위치를 찾는다.

위에서 말했던 4방향에 같은 바둑돌이 놓여져있는지 확인하고 omok 함수를 돌린다.

omok 함수

private static boolean omok(int[][] board,int i,int j,int dir) {
    int cnt=0;
    int tmp_dir=dir;

    if(dir==0){
        for(int n=0;n<6;n++){
            if(j+n>=19) break;
            if(board[i][j+n]!=board[i][j]) break;
            cnt++;

            if(n==5) break;
            result[n][0]=i;
            result[n][1]=j+n;
        }
    }else if(dir==1){
        for(int n=0;n<6;n++){
            if(i+n>=19 || j+n>=19) break;
            if(board[i+n][j+n]!=board[i][j]) break;
            cnt++;

            if(n==5) break;
            result[n][0]=i+n;
            result[n][1]=j+n;
        }
    }else if(dir==2){
        for(int n=0;n<6;n++){
            if(i+n>=19) break;
            if(board[i+n][j]!=board[i][j]) break;
            cnt++;

            if(n==5) break;
            result[n][0]=i+n;
            result[n][1]=j;
        }
    }else if(dir==3){
        for(int n=0;n<6;n++){
            if(i+n>=19 || j-n<0) break;
            if(board[i+n][j-n]!=board[i][j]) break;
            cnt++;

            if(n==5) break;
            result[n][0]=i+n;
            result[n][1]=j-n;
        }
    }

    if(cnt==5) {
        if(tmp_dir==0){
            if(j-1>=0 && board[i][j-1]==board[i][j]) {
                result=new int[5][2];
                return false;
            }
        }else if (tmp_dir==1){
            if(i-1>=0 && j-1>=0 && board[i-1][j-1]==board[i][j]) {
                result=new int[5][2];
                return false;
            }
        }else if(tmp_dir==2){
            if(i-1>=0 && board[i-1][j]==board[i][j]) {
                result=new int[5][2];
                return false;
            }
        }else if(tmp_dir==3){
            if(i-1>=0 && j+1<19 && board[i-1][j+1]==board[i][j]) {
                result=new int[5][2];
                return false;
            }
        }
        return true;
    }

    result=new int[5][2];
    return false;
}

그리고 omok 함수를 살펴보면 우선 방향별로 오목을 확인하여 cnt 값을 올려주고 이때 5개의 바둑돌 위치값이 들어갈 수 있는 result에 위치값들을 넣어준다.

이후 5개의 바둑돌을 찾게 되면 또 한번의 검증에 들어간다.

육목의 경우는 답으로 인정되지 않기 때문에 4방향에 맞춰 반대 방향에 같은 색깔의 바둑돌이 있는지 확인한 후, 육목이라면 그 동안 바둑돌의 위치값을 넣어준 result 배열을 초기화 하고 false를 반환해준다. 오목이라면 true를 반환한다.

왼쪽 및 상위 값 출력하기

if(a==-1 && b==-1){
    System.out.println(0);
}else {
    System.out.println(board[a][b]);
    
    //왼쪽, 상위
    if(result[0][0]+1==result[1][0] && result[0][1]==result[1][1]){
        System.out.println((result[0][0]+1)+" "+(result[0][1]+1));
    }else{
        int idx=0;
        
        for(int i=0;i<5;i++){
            if(result[i][1]<result[idx][1]) idx=i;
        }
        
        System.out.print((result[idx][0]+1)+" "+(result[idx][1]+1));
    }

}

Main 함수에서 오목인지 확인이 된다면 a와 b 변수에 처음 발견한 바둑돌의 위치값을 넣어준다.

a와 b의 값이 -1 이라면 오목이 완성된 바둑돌을 찾지 못했다는 뜻이 기때문에 0을 출력해주고

오목이 발견되었다면 또 한번 두 가지의 정답으로 나뉜다.

• 세로로 만들어진 오목인 경우
• 그 외의 경우

세로로 만들어진 경우라면 제일 상위의 좌표를 가져오고

이외의 상황이라면 제일 왼쪽에 있는 값을 가져온다.

세로로 된 오목이라면 오목을 찾았을 때 넣었던 첫 바둑돌의 위치값을 출력하면 되기 때문에 쉽게 찾을 수 있다.

이외의 경우라면 result 배열에서 j값 즉, 열 값이 가장 작은 위치를 구한다.

if(result[i][1]<result[idx][1]) idx=i;

위와 같은 코드를 이용하여 제일 열값이 작은 위치 인덱스를 저장해주고 해당 위치의 값을 출력한다.

이때, 출력해야하는 방식이 배열의 인덱스가 아니기 때문에 구한 위치값에서 +1씩 해준다.

6개 이상의 바둑돌이 연속해있는 경우 완전탐색을 이용하여 바둑돌이 있다면 오목을 확인하는 로직이기 때문에

4방향(오른쪽, 오른쪽 아래 대각선, 아래, 왼쪽 아래 대각선)으로 확인했을 때 5개라면 오목이라고 판단하게 된다.

예를 들어 1111111 이런 경우가 있다고 했을때, 첫번째에서부터 확인하면 5개이상의 바둑돌이 연속해 있기 때문에 오목이라고 판단하지 않는다.

하지만 세번째에서부터 확인하면 오른쪽 방향으로 5개이기 때문에 오목으로 판단하게되는 오류가 있었다.

때문에 이런 오류를 없애기 위해서는 이전의 방향에 있는 바둑돌이 있는지 확인해야했다.

---

처음에는 쉽게 구현했으나 틀리는 경우가 발생하여 하나씩 고치다보니 많은 부분을 조금씩 고쳐야했다.

문제를 풀기에 급급해서 중복되는 코드가 많이 보이는데 다른 사람들과 코드를 리뷰하면서 바꿔보려고 한다.