문제
N 개의 막대 기둥이 일렬로 세워져 있다. 기둥들의 폭은 모두 1 m이며 높이는 다를 수 있다. 이 기둥들을 이용하여 양철로 된 창고를 제작하려고 한다. 창고에는 모든 기둥이 들어간다. 이 창고의 지붕을 다음과 같이 만든다.
- 지붕은 수평 부분과 수직 부분으로 구성되며, 모두 연결되어야 한다.
- 지붕의 수평 부분은 반드시 어떤 기둥의 윗면과 닿아야 한다.
- 지붕의 수직 부분은 반드시 어떤 기둥의 옆면과 닿아야 한다.
- 지붕의 가장자리는 땅에 닿아야 한다.
- 비가 올 때 물이 고이지 않도록 지붕의 어떤 부분도 오목하게 들어간 부분이 없어야 한다.
그림 1은 창고를 옆에서 본 모습을 그린 것이다. 이 그림에서 굵은 선으로 표시된 부분이 지붕에 해당되고, 지붕과 땅으로 둘러싸인 다각형이 창고를 옆에서 본 모습이다. 이 다각형을 창고 다각형이라고 하자.
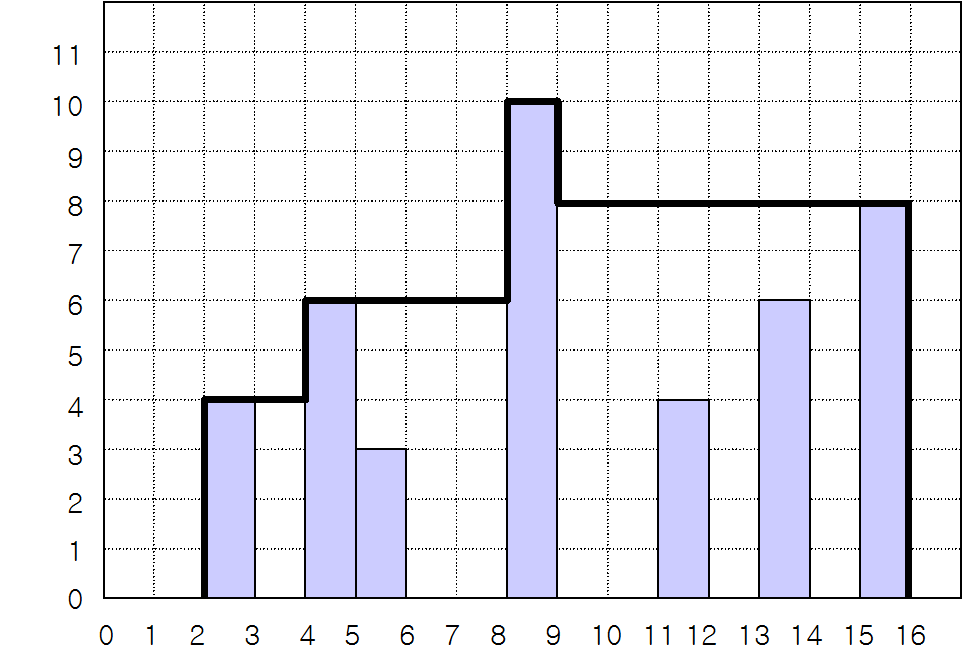
그림1 . 기둥과 지붕(굵은 선)의 예
창고 주인은 창고 다각형의 면적이 가장 작은 창고를 만들기를 원한다. 그림 1에서 창고 다각형의 면적은 98 ㎡이고, 이 경우가 가장 작은 창고 다각형이다.
기둥들의 위치와 높이가 주어질 때, 가장 작은 창고 다각형의 면적을 구하는 프로그램을 작성하시오.
입력
첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의 빈 칸을 사이에 두고 주어진다. L과 H는 둘 다 1 이상 1,000 이하이다.
출력
첫 줄에 창고 다각형의 면적을 나타내는 정수를 출력한다.
예제 입력 1
7
2 4
11 4
15 8
4 6
5 3
8 10
13 6예제 출력 1
98문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;
public class BJ2304 {
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N=Integer.parseInt(br.readLine());
int[][] square=new int[N][2];
int max=Integer.MIN_VALUE;
for(int i=0;i<N;i++){
st=new StringTokenizer(br.readLine());
square[i][0]=Integer.parseInt(st.nextToken());
square[i][1]=Integer.parseInt(st.nextToken());
if(max<square[i][1]) max=square[i][1];
}
Arrays.sort(square, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0]-o2[0];
}
});
//max의 높이인 기둥이 여러개일 수 있음
ArrayList<Integer> list=new ArrayList<>();
//idx 위치 찾기
for(int i=0;i<N;i++){
if(square[i][1]==max){
list.add(i);
}
}
//list 모두 사용
int result=0;
int maxArea=0;
int x1=square[0][0];
int y1=square[0][1];
//max 높이의 좌
for(int i=1;i<=list.get(0);i++){
if(y1<square[i][1]){
//높이가 더 높을때
result+=y1*(square[i][0]-x1);
x1=square[i][0];
y1=square[i][1];
}
}
int x2=square[N-1][0];
int y2=square[N-1][1];
//max 높이의 우
for(int i=N-2;i>=list.get(list.size()-1);i--){
if(y2<square[i][1]){
result+=y2*(x2-square[i][0]);
x2=square[i][0];
y2=square[i][1];
}
}
if(list.size()==1){
maxArea=max;
}else {
int a = list.get(list.size() - 1);
int b = list.get(0);
maxArea = max * (square[a][0] - square[b][0] + 1);
}
System.out.println(result+maxArea);
}
}이 문제를 풀 때 중요하게 고려해야할 점은 아래와 같다.
- 오목한 부분이 없어야한다
- 가장 높은 기둥
가장 높은 기둥 저장
Arrays.sort(square, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0]-o2[0];
}
});
//max의 높이인 기둥이 여러개일 수 있음
ArrayList<Integer> list=new ArrayList<>();
//idx 위치 찾기
for(int i=0;i<N;i++){
if(square[i][1]==max){
list.add(i);
}
}기둥의 위치별로 배열에 정렬시켜주고
가장 높은 기둥의 개수가 여러개라면 배열에 모두 저장해주어 필요한 부분이 있으면 사용한다.
우선은 가장 높은 기둥이 한 개이고 중간에 위치한 경우의 코드를 살펴보자
int result=0;
int maxArea=0;
int x1=square[0][0];
int y1=square[0][1];
//max 높이의 좌
for(int i=1;i<=list.get(0);i++){
if(y1<square[i][1]){
//높이가 더 높을때
result+=y1*(square[i][0]-x1);
x1=square[i][0];
y1=square[i][1];
}
}
int x2=square[N-1][0];
int y2=square[N-1][1];
//max 높이의 우
for(int i=N-2;i>=list.get(list.size()-1);i--){
if(y2<square[i][1]){
result+=y2*(x2-square[i][0]);
x2=square[i][0];
y2=square[i][1];
}
}
if(list.size()==1){
maxArea=max;
}
System.out.println(result+maxArea);어차피 가장 높은 기둥에서 높이가 갈리게되기 때문에 좌, 우로 나누어 각 면적을 구해준 다음 max 높이의 기둥의 면적도 추가해줘야하기 때문에 좌+우+가장 높은 높이의 기둥 값을 출력해주면 된다.
하지만 가장 높은 기둥이 여러개일 수 있기 때문에 그 점을 고려해야하는데
높은 기둥이 여러개일 경우에는 지붕의 오목한 부분이 생기면 안되기 때문에 max 높이의 기둥이 시작하는 점에서 끝나는 위치까지 max 높이를 가지는 면적이 생기게 될 것이다.
즉, 가장 높은 높이의 기둥들 중 처음 위치의 기둥과 마지막 기둥만 고려하면 된다는 뜻이다.
else{
int a=list.get(list.size()-1);
int b=list.get(0);
maxArea=max*(square[a][0]-square[b][0]+1);
}위 코드의 마지막 if문에 else를 추가해주어 그 면적을 구해주면 된다.
