홈 방범 서비스

조소복·2022년 11월 9일

2117번 Java SWEA 자바

문제

N*N 크기의 도시에 홈방범 서비스를 제공하려고 한다.

홈방범 서비스는 운영 상의 이유로 [Fig. 1]의 파란색 부분과 같이 마름모 모양의 영역에서만 제공된다.

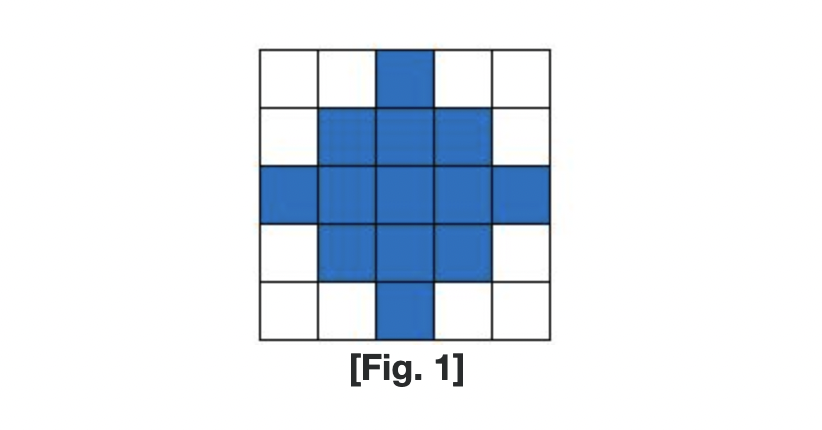
또한, 홈방범 서비스를 제공하기 위해서는 운영 비용이 필요하다.

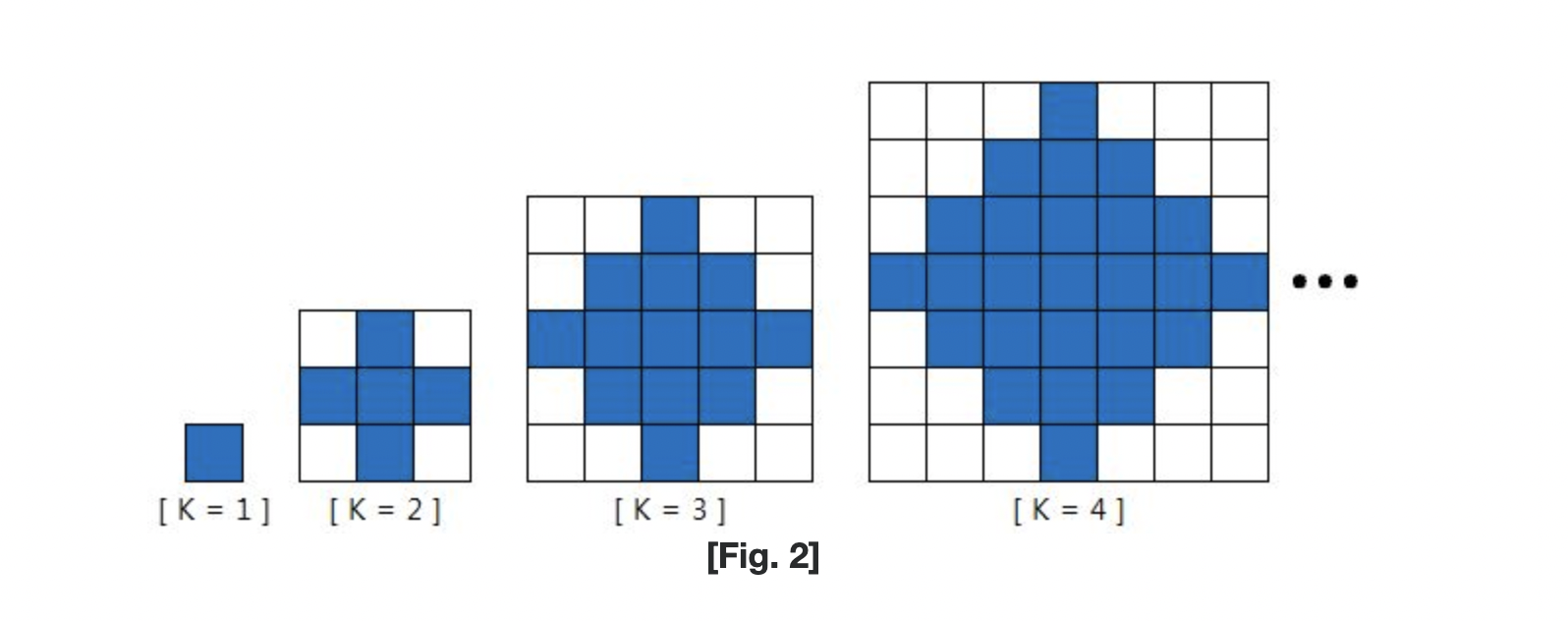
[Fig. 2]와 같이 서비스 영역의 크기 K 가 커질수록 운영 비용이 커진다.

운영 비용은 서비스 영역의 면적과 동일하며, 아래와 같이 구할 수 있다.

운영 비용 = K K + (K - 1) (K - 1)

운영 영역의 크기 K 는 1 이상의 정수이다.

K = 1 일 때, 운영 비용은 1 이다.
K = 2 일 때, 운영 비용은 5 이다.
K = 3 일 때, 운영 비용은 13 이다.
K = 4 일 때, 운영 비용은 25 이다.

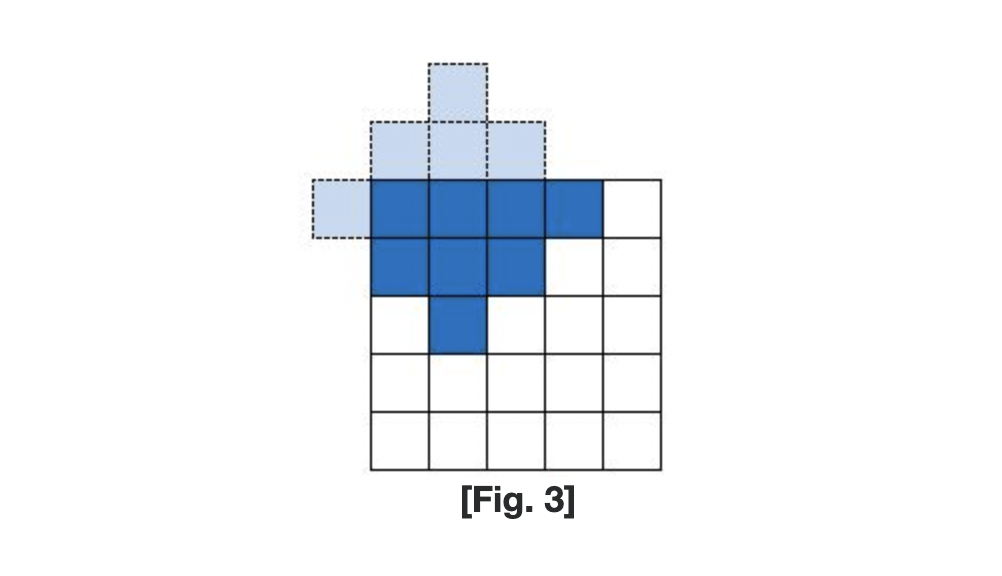
[Fig. 3]과 같이 도시를 벗어난 영역에 서비스를 제공해도 운영 비용은 변경되지 않는다.

[Fig. 3]의 경우 K = 3 이므로, 운영 비용은 13 이다.

홈방범 서비스를 제공받는 집들은 각각 M의 비용을 지불할 수 있어, 보안회사에서는 손해를 보지 않는 한 최대한 많은 집에 홈방범 서비스를 제공하려고 한다.

도시의 크기 N과 하나의 집이 지불할 수 있는 비용 M, 도시의 정보가 주어진다.

이때, 손해를 보지 않으면서 홈방범 서비스를 가장 많은 집들에 제공하는 서비스 영역을 찾고,

그 때의 홈방범 서비스를 제공 받는 집들의 수를 출력하는 프로그램을 작성하라.

[예시]

예를 들어, [Fig. 4]과 같이 N이 8인 도시의 정보가 주어지고, 하나의 집이 지불할 수 있는 비용 M이 3이라고 생각해 보자.

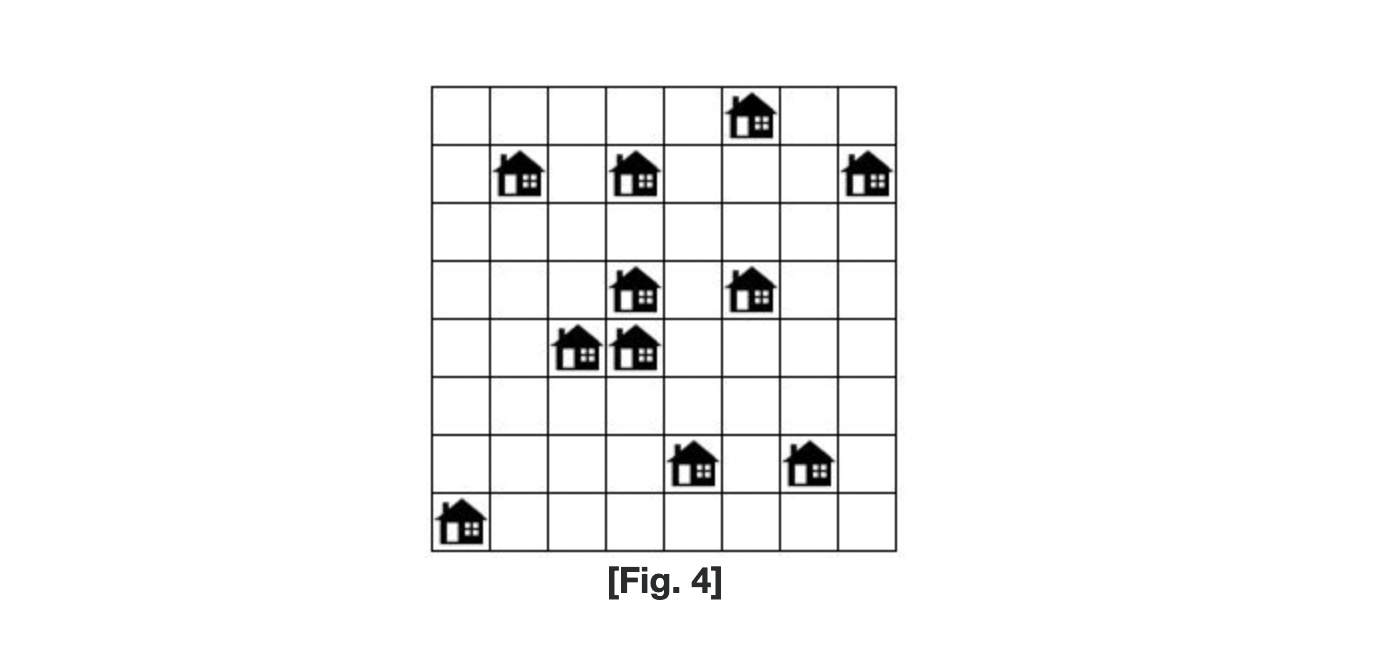
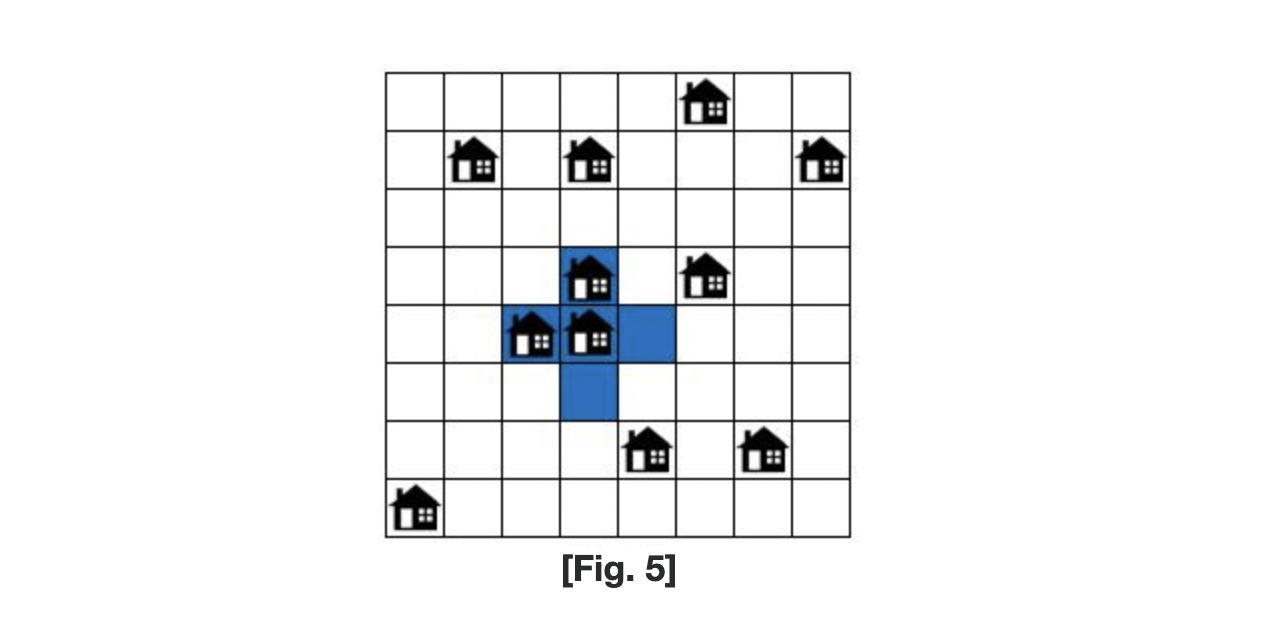
[Fig. 5]와 같이 서비스 영역 K = 2로 하여 홈방범 서비스를 제공할 때는 최대 3개의 집까지 서비스 제공이 가능하다.

이 경우 보안회사의 이익은 4가 되어 손해를 보지 않고 서비스 제공이 가능하다.

보안회사의 이익(4) = 서비스 제공받는 집들을 통해 얻는 수익(3*3) - 운영 비용(5)

[Fig. 6]은 서비스 영역 K = 3으로 하여 홈방범 서비스를 제공할 때에 최대 5개의 집까지 서비스 제공이 가능한 경우 중 하나이다.

보안회사의 이익(2) = 서비스 제공받는 집들을 통해 얻는 수익(3*5) - 운영 비용(13)

위의 예에서, 보안회사가 손해를 보지 않고 서비스 가능한 최대 집의 수는 5이며, 5가 정답이 된다.

[제약사항]

시간제한 : 최대 50개 테스트 케이스를 모두 통과하는데, C/C++/Java 모두 3초
도시의 크기 N은 5 이상 20 이하의 정수이다. (5 ≤ N ≤ 20)
하나의 집이 지불할 수 있는 비용 M은 1 이상 10 이하의 정수이다. (1 ≤ M ≤ 10)
홈방범 서비스의 운영 비용은 서비스 영역의 면적과 동일하다.
도시의 정보에서 집이 있는 위치는 1이고, 나머지는 0이다.
도시에는 최소 1개 이상의 집이 존재한다.

[입력]

입력의 맨 첫 줄에는 총 테스트 케이스의 개수 T가 주어지고, 그 다음 줄부터 T개의 테스트 케이스가 주어진다.

각 테스트 케이스의 첫 번째 줄에는 도시의 크기 N과 하나의 집이 지불할 수 있는 비용 M이 주어진다.

그 다음 줄부터 N*N 크기의 도시정보가 주어진다. 지도에서 1은 집이 위치한 곳이고, 나머지는 0이다.

[출력]

테스트 케이스의 개수만큼 T줄에 T개의 테스트 케이스 각각에 대한 답을 출력한다.

각 줄은 "#x"로 시작하고 공백을 하나 둔 다음 정답을 출력한다. (x는 1부터 시작하는 테스트 케이스의 번호이다)

출력해야 할 정답은 손해를 보지 않으면서 홈방범 서비스를 가장 많은 집들에 제공하는 서비스 영역을 찾았을 때,

그 때의 서비스를 제공 받는 집들의 수이다.

문제 풀이

import java.awt.*;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;

public class SW2117 {
    static int homeCount;
    static int N,M;
    static int[][] moves={{0,1},{0,-1},{1,0},{-1,0}};
    static int[][] map;

    public static void main(String[] args) throws IOException {
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        int T=Integer.parseInt(br.readLine());

        for(int t=1;t<=T;t++){
            homeCount=0;
            st=new StringTokenizer(br.readLine());
            N=Integer.parseInt(st.nextToken());
            M=Integer.parseInt(st.nextToken());

            map=new int[N][N];

            for(int i=0;i<N;i++){
                st=new StringTokenizer(br.readLine());
                for(int j=0;j<N;j++){
                    map[i][j]=Integer.parseInt(st.nextToken());
                }
            }

            // 서비스 영역 탐색
            for(int k=1;k<=N+1;k++){
                // 서비스 영역 당 최대한 많은 집들을 포함하는 위치 선정
                //가운데 지점을 모든 칸 다 돌려보기
                for(int i=0;i<N;i++){
                    for(int j=0;j<N;j++){
                        //집 몇 채 있는지 확인
                        bfs(i,j,k);
                    }
                }
            }

            System.out.println("#"+t+" "+homeCount);

        }

    }

    private static void bfs(int i, int j, int k) {
        Queue<Point> queue=new ArrayDeque<>();
        boolean[][] visited=new boolean[N][N];
        queue.offer(new Point(i,j));

        // 집 개수
        int count=0;

        if(map[i][j]==1){
            count++;
            visited[i][j]=true;
        }

        while(!queue.isEmpty()){
            Point n=queue.poll();

            for(int d=0;d<4;d++){
                int nx=n.x+moves[d][0];
                int ny=n.y+moves[d][1];

                if(nx<0 || nx>=N || ny<0 || ny>=N) continue;

                if(Math.abs(nx-i)+Math.abs(ny-j)<k && !visited[nx][ny]){
                    if(map[nx][ny]==1){
                        count++;
                    }
                    queue.offer(new Point(nx,ny));
                    visited[nx][ny]=true;
                }

            }
        }

        if(homeCount<count){
            int cal=k*k+(k-1)*(k-1);
            if((M*count-cal)>=0){
                homeCount=count;
            }
        }
    }
}

서비스영역에 따라 손해를 보지 않는 상황에서 최대한 많이 서비스할 수 있는 집의 개수를 구하는 문제였다.

즉, 서비스영역의 크기가 정해져있지 않고 어느 지점에서부터 퍼져나가는지 정해져있지 않기 때문에

모든 서비스 영역의 크기와, 시작되는 위치를 모두 고려하여 값을 구해야한다.

서비스 영역의 크기와 위치

// 서비스 영역 탐색
for(int k=1;k<=N+1;k++){
    // 서비스 영역 당 최대한 많은 집들을 포함하는 위치 선정
    //가운데 지점을 모든 칸 다 돌려보기
    for(int i=0;i<N;i++){
        for(int j=0;j<N;j++){
            //집 몇 채 있는지 확인
            bfs(i,j,k);
        }
    }
}

서비스 영역의 크기는 1부터 시작하여 모든 경우의 수를 따져봐야한다.

이때, k의 범위를 잘 설정해야하는데 서비스 영역의 크기가 N*N의 크기를 모두 덮는 경우까지도 생각해야하기 때문에 N+1까지 범위를 잡아야한다.

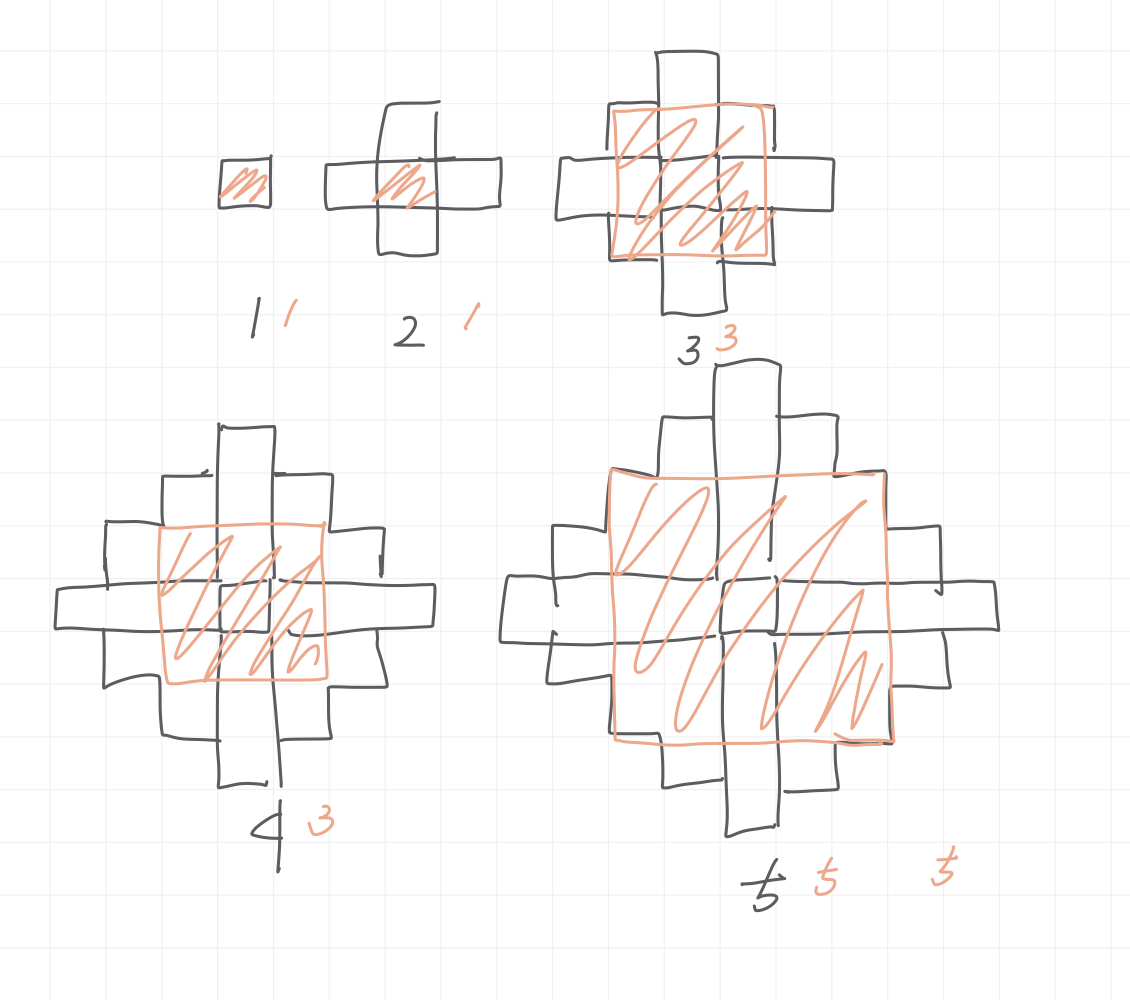
위의 사진처럼 k의 크기에 따라 가운데 정사각형의 크기를 생각하면 1, 1, 3, 3, 5, 5... 의 규칙을 따라 증가하는 것을 확인할 수 있다.

즉, N이 짝수라면 k의 크기는 N+1이기 때문에 반복문을 돌리기위해 k의 범위를 N+1까지 잡아줘야한다.

k의 범위를 잡았다면 지도의 위치를 처음부터 서비스 영역의 가운데 위치로 지정해주어 범위 내 집의 개수를 탐색한다.

-> 이때, BFS 사용

집의 개수 탐색

private static void bfs(int i, int j, int k) {
    Queue<Point> queue=new ArrayDeque<>();
    boolean[][] visited=new boolean[N][N];
    queue.offer(new Point(i,j));

    // 집 개수
    int count=0;

    if(map[i][j]==1){
        count++;
        visited[i][j]=true;
    }

    while(!queue.isEmpty()){
        Point n=queue.poll();

        for(int d=0;d<4;d++){
            int nx=n.x+moves[d][0];
            int ny=n.y+moves[d][1];

            if(nx<0 || nx>=N || ny<0 || ny>=N) continue;

            if(Math.abs(nx-i)+Math.abs(ny-j)<k && !visited[nx][ny]){
                if(map[nx][ny]==1){
                    count++;
                }
                queue.offer(new Point(nx,ny));
                visited[nx][ny]=true;
            }

        }
    }

    if(homeCount<count){
        int cal=k*k+(k-1)*(k-1);
        if((M*count-cal)>=0){
            homeCount=count;
        }
    }
}