1. 스케줄링 문제에 접근하는 이진 탐색 트리 소개
이진 탐색 트리(BST, Binary Search Tree)란?
탐색작업을 효율적으로 하기 위한 자료구조
이진탐색를 중위순회하면 오름차순으로 정렬된 값을 얻을 수 있다
– key(왼쪽서브트리)≤key(루트노드)≤key(오른쪽서브트리)
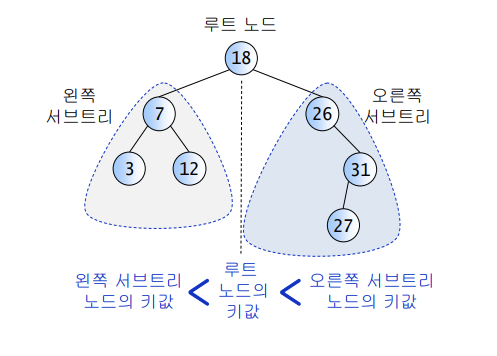
binary search tree로 찾을 때 갖출 조건
– 완전 이진 트리(거의 완전 이진트리 x)
– 왼쪽 노드 key <= 오른쪽 노드 key
모든 노드 x에 대하여 if y가 x의 left subtree에 있다면 key(y) <= key(x)
if y가 x의 right subtree에 있다면 key(y) >= key(x)
max heap 일때는 부모 key >= 자식 key
탐색 연산
비교한 결과가 같으면 탐색이 성공적으로 끝난다
키 값이 루트보다 작으면 ➔ 왼쪽 자식을 기준으로 다시 탐색
키 값이 루트보다 크면 ➔ 오른쪽 자식을 기준으로 다시 탐색
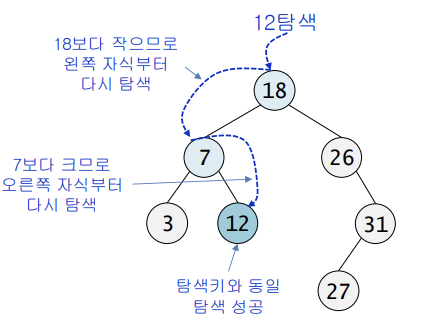
구현 방법
'순환적인 구현', '반복적인 구현', '일반 함수 구현', '트리의 멤버함수 구현', '노드의 멤버함수 구현'
삽입 연산
이진 탐색 트리에 원소를 삽입하기 위해서는 먼저 탐색을 수행하는 것이 필요하다
➔ 탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치
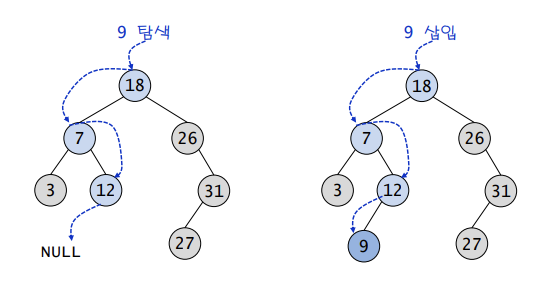
삭제 연산
삭제 연산에서는 3가지 경우가 있다
1.삭제하려는 노드가 단말 노드일 경우
➔ 단말노드의 부모노드를 찾아서 연결을 끊으면 된다

2.삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리중 하나만
가지고 있는 경우
➔ 노드는 삭제하고 서브 트리는 부모 노드에 붙여준다

3.삭제하려는 노드가 두개의 서브 트리 모두 가지고 있는 경우
➔ 가장 비슷한 값을 가진 노드를 삭제 노드 위치로 가져오고 후계 노드를 선택한다

노드 18을 삭제하는 방법

이진 탐색 트리의 성능
이진 탐색 트리의 시간 복잡도는 트리의 높이인 h에 비례한다
따라서 높이를 최소한으로 만들어야 알고리즘이 빨라진다 left(h)와 right(h)가 비슷해야 좋은 알고리즘
O(logn) ➔ 최선의 알고리즘
O(n) ➔ 최악의 알고리즘
예시
각 오븐에 3분(t) 있으면 완성된다
4,20(현재),32,37,45(R)분에 휘낭시에가 들어간다면 33분, 40분에 각각 새 휘낭시에가 들어가도 되는가?
답변 : 33분은 불가능 하지만 40분은 가능함
이유: 32분에 휘낭시에가 오븐에 들어가면 3분 뒤인 35분에 넣을 수 있기 때문에 33분은 넣을 수 없고 또한 37분에 넣으면 3분 뒤인 40분에 새로운 휘낭시에가 들어갈 수 있어 40분은 가능하다
이때 새 휘낭시에를 넣을 수 있는지 없는지는 이진 탐색 트리를 이용하여 찾으면 된다
➔ 각 노드의 본인을 포함한 자식 노드가 몇개인지 확인하고 root에서 value찾을 때까지 내려온다
2. Big-O 소개
Big-O란?
알고리즘의 효율성을 표기해주는 표기법, 알고리즘이 얼마나 빨리 작동하는지 알기 위해 사용한다
여기서 컴퓨터 구조/흐르는 시간과는 무관하고 오로지 input size x (절대값 x)와 연관있다
boundary(upper bound=loose bound)'최악의 경우 여기까지 걸린다'를 알 수 있다
가장 큰 차수만을 이용하여 표현한다
O(n)은 input이 들어오는 만큼 linear(선형적)으로 변한다
➔ O(log n)으로 표현되는 것이 가장 좋은 알고리즘이다
n ➔ long term(긴시간동안)일 때(log밑은 2로 생각한다)
Big-O는
(lower bound) 0(1), O(log n), O(n), O(nlog n), 0(n^2), O(n^n), O(2^n) (upper bound)
순으로 좋다
– n! = nx(n-1)x(n-2).....X1 big-o 표현 방법은 o(n)이다
– if n<=0 일때 1로 return, else nxf(n-1) return ➔ big-o는 o(n)이다
– if n<=0일때 1로 return, else return f(n/2)+1 ➔ big-0는 o(log n)이다
정렬되지 x 배열
체크 안해도 될 때(그냥 체크 안하고 들어가고 싶은데 들어갈때, 거의 사용하지 않음) ➔ o(1)
체크해야할 때 ➔ o(n)
정렬된 배열
1. search min R[i] >= t(binary search를 사용) ➔ O(log n)
2. compare R[i-1],R[i] k 비교 (앞 뒤 비교) ➔O(1)
3. insert ➔ O(n)
list
compare, insert ➔ O(1)
search ➔ O(n)
heap ➔ O(n)
3. 문제 풀이
3-1. LeetCode 98, 99, 700, 701
98 : 주어진 트리가 이진 탐색 트리인지 확인


99 : 한 쌍의 노드를 swap하여 이진 탐색 트리로 만들기
Inorder Traversal로 먼저 vector에 값 넣어주고
하나씩 탐색하면서 역전되는 곳 찾기
역전되는 곳 1pair -> 첫 번째 값이 first, 두번째 값이 second로 가정
역전되는 곳 2pair -> 첫 번째 pair의 첫 번째 값이 first, 두 번째 pair의 두 번째 값이 second로 가정


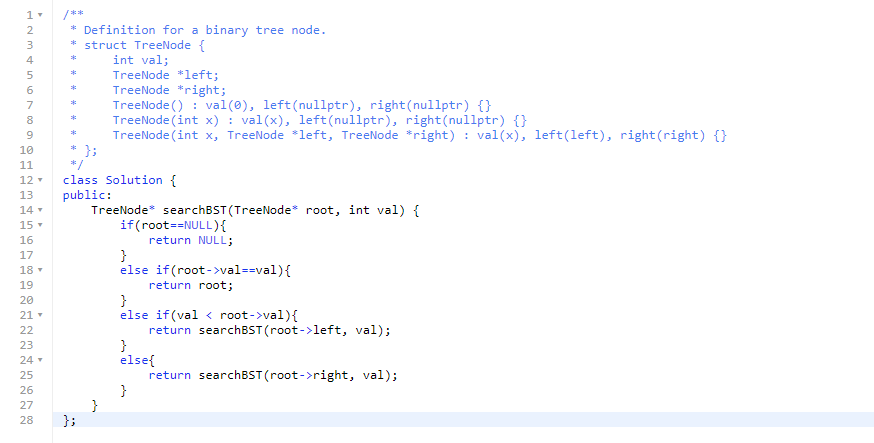
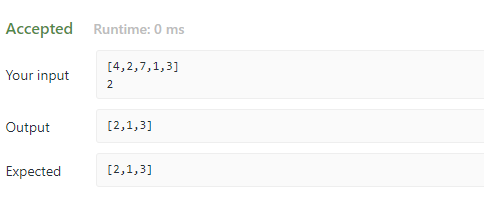
700 : 이진 탐색 트리에서 val과 같은 값 찾기
val과 같은 노드가 있다면 해당 노드와 그 노드의 자식 노드 값 까지 출력
val과 같은 노드가 없다면 null를 출력
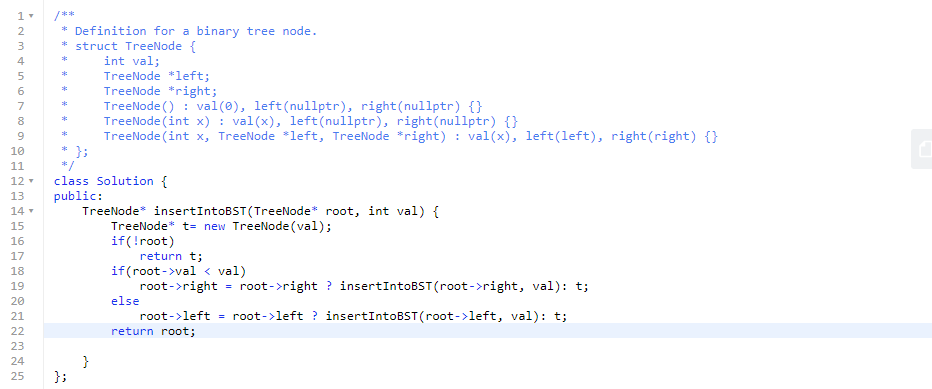
701 : 이진탐색트리에서 특정 값을 올바른 노드에 삽입 후 root를 반환하는 문제

도움받은 곳
https://www.youtube.com/watch?v=XYjQ8EB7yik
https://www.youtube.com/watch?v=2ahCLZ3x1iI
https://jungahshin.tistory.com/83
https://luckydavekim.github.io/algorithm/leetcode/validate-binary-search-tree
https://ifuwanna.tistory.com/
다음에 시간이 된다면 백준 문제 5639번과, 1539번을 풀어볼 것이다
