[백준/Python3] 2004 조합 0의 개수

https://www.acmicpc.net/problem/2004

---

풀이

조합 결과의 끝에서 부터 0이 아닐 때까지의 0의 개수를 구하는 문제다. 문제에서 무엇을 구할 지는 명확한데에 비해 간단하게 팩토리얼로 풀려고 하면 최대 2,000,000,000(...)의 재귀를 해야한다. 당연히 문제는 풀리지 않으므로 다른 방법을 생각하자.

중요한건 조합의 결과를 구하는게 목적이 아니라 뒤에서 부터 0이 아닐 때 까지의 0의 개수를 구하는게 목적이라는 점이다. 우리가 잘 알다시피 끝에 0이 나올려면 기본적으로 10의 배수여야한다. 10을 소인수분해하면 2와 5로 나타나니 중요한건 2와 5의 개수다. 그리고 5 보다는 0이 나올 수 있도록 2의 개수가 중요하다. 그렇다면 어떻게 2와 5의 개수를 구해야 하는가?

10!에서 2의 개수를 구하는 것으로 예를 들어보자.

10! = 1 * 2 * 3 * ... * 9 * 10 

으로 나타난다. 여기서 2를 인수로 가지는 수로만 보면 아래와 같이 확인할 수 있다.

10! -> 2 4 6 8 10

여기서 필요 없는 다른 인수들을 제거하고 2 만 남길 경우,

10! -> 2^1 2^2 2^1 2^3 2^1

로 나타낼 수 있다.

2가 한 번이라도 곱해진 수는 2, 4, 6, 8, 10
2가 두 번이상 곱해진 수는 = 4, 8
2가 세 번이상 곱해진 수는 = 8 로,

총 5 + 2 + 1 = 8개의 2가 인수로 들어있는 것을 확인할 수 있다.

위 개수는 10//2 = 5, 5//2 = 2, 2//2 = 1로 나타낼 수 있다.

이를 함수로 변환하면

def count_2(target, 2):
    count = 0
    while target:
        target = target // 2
        count = count + target
    return count

5 역시 위와 같은 방법으로 인수의 개수를 구할 수 있다.

이제, 조합에서 인수의 개수를 확인해야 한다.

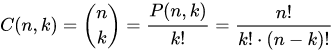
어떤 수에서 특정 수로 나눌 경우 인수의 개수는 뺄셈으로 계산되므로 n, k, n-k의 2, 5 인수의 개수를 구한 뒤 뺄셈을 해준다.

이렇게 구한 5와 2의 인수 개수에서 10으로 표현될 수 있는 인수의 개수는 5와 2, 둘 중 작은 인수의 개수로 구할 수 있다.

코드

def count_num(target, num):
    count = 0
    while target:
        target = target // num
        count = count + target
    return count

n, m = map(int, input().split())

n_2 = count_num(n, 2)
n_5 = count_num(n, 5)

r_2 = count_num(n-m, 2)
r_5 = count_num(n-m, 5)

m_2 = count_num(m, 2)
m_5 = count_num(m, 5)

count_5 = n_5 - r_5 - m_5
count_2 = n_2 - r_2 - m_2

print(min(count_5, count_2))