최단 경로 길이 찾기

<문제>

오로지 오른쪽 혹은 아래로만 이동하여 맨위 왼쪽끝 -> 맨아래 오른쪽끝으로 가는 최단 경로의 길이를 계산한다.

//예시 배열
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]

 경로: 1→3→1→1→1
 답: 7

<풀이>

새로운 배열을 매핑하려 한다. 단, 각 index의 값은 지나온 경로의 길이로 둘 것이다.

예시)
[0][0]->[0][1]로 갔다면  1+3=4
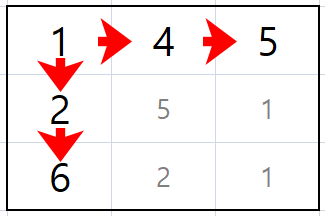
[0][0]->[0][1]->[0][2]로 갔다면 1+3+1=5

우선 맨 윗줄과 맨 왼쪽 줄만 생각해보자.

이들은 더 위와 더 왼쪽이 존재하지 않으니 오로지 왼쪽에서 오른쪽으로만, 위에서 아래로만 지나간다. 길이의 배열로 새롭게 그려보면 다음과 같다.

그러면 이제 각 index를 기준으로 생각해보자.
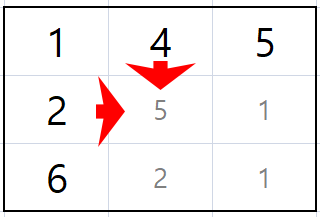
갈 수 있는 방향이 오른쪽 혹은 아래로 정해져 있다는 것은 반대로 생각했을 때 오는 방향도 각 index의 왼쪽과 위로 정해져 있다는 뜻이다.

예를 들어, [1][1]로 올 수 있는 방향은 [0][1] 혹은 [1][0] 두 가지이다.

이걸 새 배열에 넣어보자.

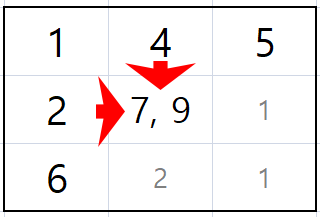
더 짧은 경로의 길이를 구하는 것이니 이 중 필요한 것은 둘 중 더 작은 7이다.

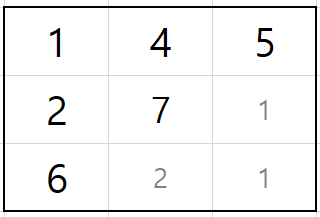
이제 이걸 반복해서 끝까지 채워나가면 된다.

const minPathSum = grid => {
  //새로 그려줄 배열 선언
  let arr = new Array(grid.length);
  for(let i = 0; i < grid.length; i++) {
    arr[i] = new Array(grid[0].length);
  }
  arr[0][0] = grid[0][0]
  
  //맨 윗줄 채워주기
  for(let i = 1; i < grid.length; i++) {
    arr[i][0] = arr[i-1][0] + grid[i][0];
  }
  
  //맨 왼쪽줄 채워주기
  for(let j = 1; j < grid[0].length; j++) {
    arr[0][j] = arr[0][j-1] + grid[0][j];
  }
  
  //두 방향에서 오는 것 중 작은 값 저장
  for(let i = 1; i < grid.length; i++) {
    for(let j = 1; j < grid[0].length; j++) {
      arr[i][j] = Math.min(arr[i-1][j], arr[i][j-1]) + grid[i][j];
    }
  }
  
  return(arr[grid.length - 1][grid[0].length - 1]);
};