[BOJ] 2745 진법 변환 JAVA

cs학생이라면 누구나 접해보았을 수의 체계!

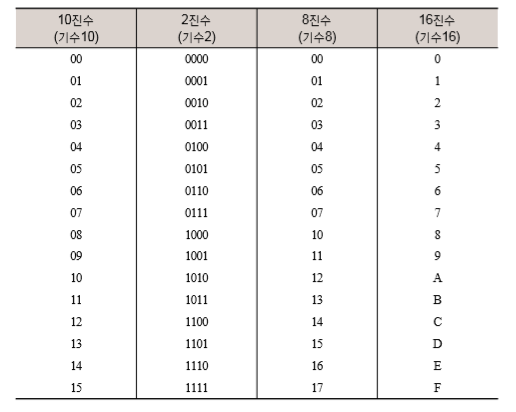
예를 들어 10진수 13을 8진수로 표현하면 15인데, 이는 (1 (8^1) + 5 (8^0)) 로 계산한다.

이를 활용하여 주어진 문제를 푼다.
문제에서는 0~9진법을 초과하는 경우(알파벳) 역시 포함하였기 때문에 이를 분리하여 if문을 작성해야한다.

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bfw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

            st = new StringTokenizer(bfr.readLine());
            String n = st.nextToken();
            int b = (Integer.parseInt(st.nextToken()));

            int sum = 0;
            int k=0;
            for(int i = n.length()-1;i>=0;i--){
                char c = n.charAt(i); //i번째 문자를 받아옴
                if(c>='0' && c<='9'){
                    sum += (c-'0') * Math.pow(b,n.length()-i-1);
                }else{
                    sum += (c-'A'+10) * Math.pow(b,n.length()-i-1);
                }
            }

        bfw.write(sum+"");
        bfr.close();
        bfw.flush();
        bfw.close();
    }
}

⚡ if(c>='0' && c<='9'), 즉 0~9진법인 경우

받아온 char에서 '0'을 뺀다.
(이 때 0의 아스키코드 48을 빼주어도 될 것 같다.)
그런다음 Math.pow(b,n.length()-i-1), b(진수)의 n.length()-i-1 제곱을 곱하여 sum에 더한다.

⚡ else, 즉 0~9진법이 아닌 경우(이 문제에서는 알파벳)

받아온 char에서 'A'를 뺀 다음 10을 더한다. (10부터 A이므로...)
그런다음 Math.pow(b,n.length()-i-1), b(진수)의 n.length()-i-1 제곱을 곱하여 sum에 더한다. 이는 위 0~9진법인 경우와 같다.

.
.

🚩 Math.pow(base, exponent)
base 값을 exponent 값으로 거듭제곱한 숫자 값

Math.pow(7, 2);    // 49
Math.pow(7, 3);    // 343
Math.pow(2, 10);   // 1024