Sorting Algorithm (Bubble, Selection, Quick Sort) w.JAVA

Sorting?

Sorting(정렬)은 원소들을 일정한 순서대로 재배치하는 것

정렬 알고리즘 (Sorting Algorithm)

• 컴퓨터에서, 가장 많이 이용되는 연산 중 하나
• 자료검색의 효율성 제고, 실용성, 이론 설명 등을 위해서도, 정렬 알고리즘이 필요함
• 수행하는 다양한 알고리즘들이 있으며, 100개 이상의 정렬 알고리즘들이 개발되어 왔음

정렬 알고리즘의 구성 요소

• 비교 연산 (compare) : 키 값 비교
• 이동 연산 (swap) : 키 값 비교 후, 자료의 위치 바꿈(교환)

public static void swap(int[] arr, int idx1, int idx2) {
	int tmp = arr[idx1];
    arr[idx1] = arr[idx2];
    arr[idx2] = tmp;
}

정렬 알고리즘의 종류

Bubble Sort (버블 정렬)

버블 정렬은 원소를 기준으로 다음 원소와 비교하며 swap한다.
마지막 원소부터 정렬된다.
1번째와 2번째, 2 번째와 3번째... n-1번째와 n번째를 정렬 한 뒤,
다시 ~ n-2번째와 n-1번째를 정렬하는 방식으로 최대 n(n-1) / 2 번 정렬한다.

💥 따라서 시간복잡도는 O(n^2)

버블 정렬은 이미 정렬되어있는 경우를 제외하고 거의 모든 상황에서 최악의 성능을 보인다.
따라서 실제 개발에서는 거의 쓰이지 않는다.

public static void sortByBubbleSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) { 
        //i를 빼는 이유는 이미 정렬된 원소를 제외하기 위함이다.
            if (arr[j] > arr[j + 1]) {
                swap(arr, j, j + 1);
            }
        }
    }
}

Selection Sort (선택 정렬)

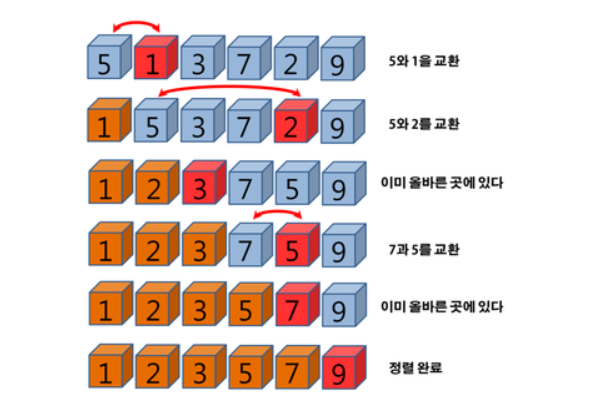
선택 정렬은 맨 앞에 들어갈 원소를 찾아 swap 한다.
1번째부터 끝까지 훑어 가장 작은 것을 첫번째로 이동하여 첫번째 원소 정렬을 완료,
2번째부터 끝까지 훑어 가장 작은 것을 두번째로 이동하여 두번째 원소 정렬을 완료...
를 n-1번 반복한다.
어떻게 정렬이 되어있든 n(n-1) / 2 에 비례하는 시간이 걸린다.

💥 따라서 시간복잡도는 O(n^2)

비교는 버블정렬과 같이 모두 이뤄지지만 swap이 이뤄지지 않으므로 버블정렬보다 두 배 정도 빠르다.

public static void sortBySelectionSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        int minIdx = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIdx]) {
                minIdx = j;
            }
        }
        swap(arr, i, minIdx);
    }
}

Quick Sort (퀵 정렬)

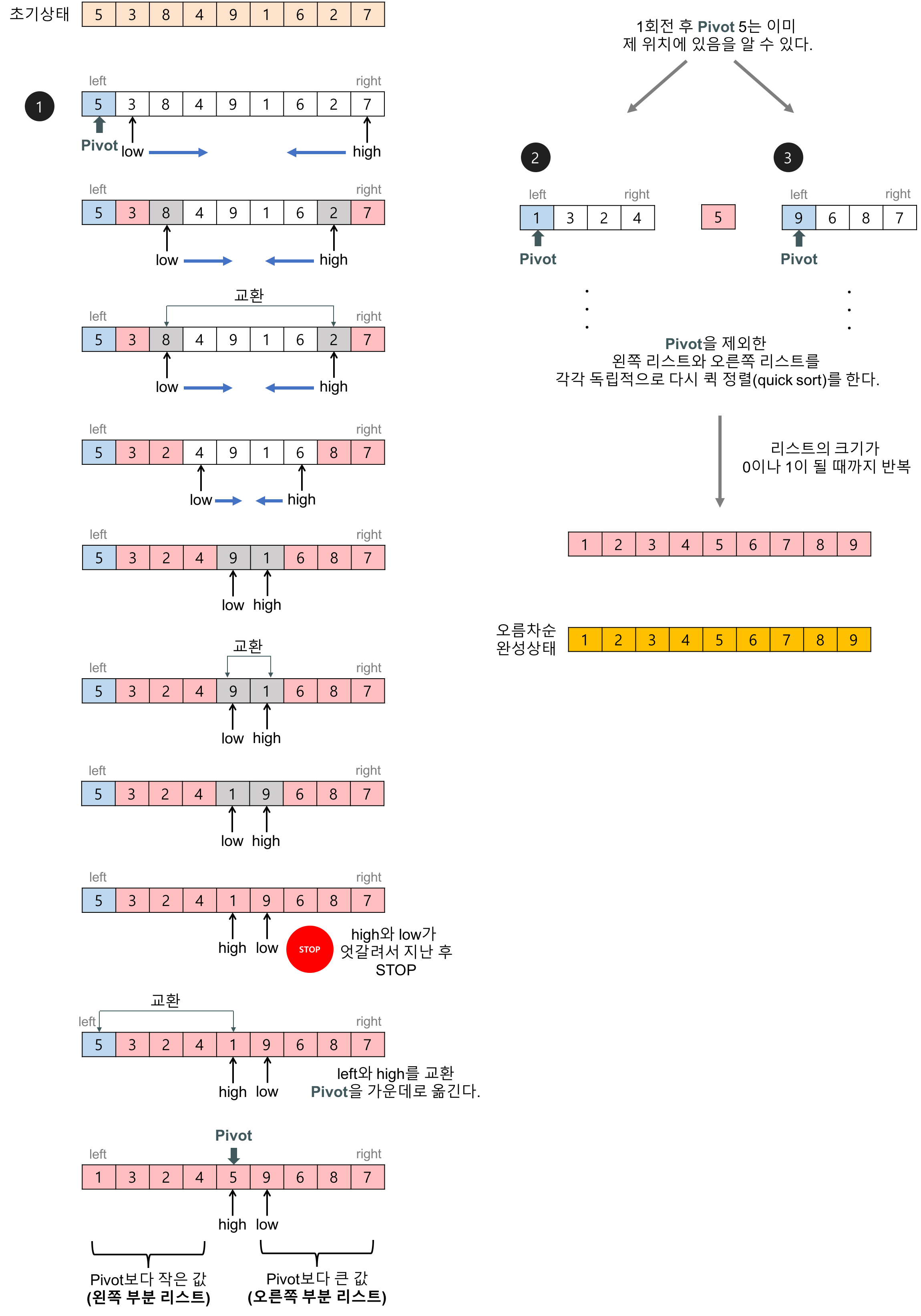
피벗을 이용한 정렬 알고리즘으로, 분할 정복 알고리즘이다.
피벗을 기준으로 피벗보다 작은 값과 큰 값의 리스트로 분할한다.
평균적인 상황에서 최고의 성능을 나타내나, 최악의경우 피벗을 최소, 혹은 최대로 선택하여 한쪽으로 배열이 모두 쏠릴 수 있다.

💥 따라서 최악의 경우 시간복잡도는 O(n^2)-> 피벗이 최소 또는 최대
, 평균의 경우 시간 복잡도는 nlogn

public static void sortByQuickSort(int[] arr) {
    quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int left, int right) {
    int part = partition(arr, left, right);
    if (left < part - 1) {
        quickSort(arr, left, part - 1);
    }
    if (part < right) {
        quickSort(arr, part, right);
    }
}
public static int partition(int[] arr, int left, int right) {
    int pivot = arr[(left + right) / 2];
    while (left <= right) { //left와 right가 
        while (arr[left] < pivot) {
            left++; //left의 값이 피벗보다 클 때 까지 증가하면서 찾기
        }
        while (arr[right] > pivot) {
            right--; //right의 값이 피벗보다 작을 때 까지 감소하면서 찾기
        }
        if (left <= right) {
            swap(arr, left, right);
            left++;
            right--;
        }
    }
    return left;
}