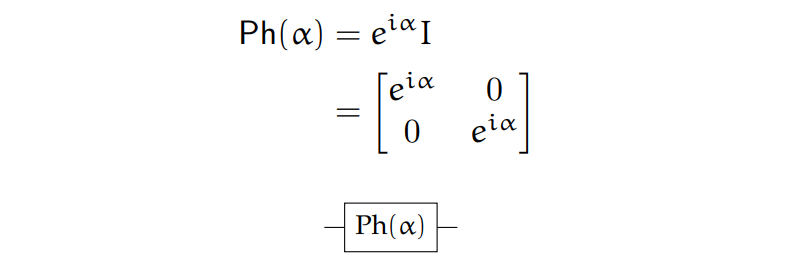Qubit 큐비트
이전 포스팅에서 컴퓨터에서 정보저장의 기본 단위가 bit라고 했다.
큐비트는 양자컴퓨터에서 정보저장의 기본 단위이다.
bit 는 0 또는 1 의 두가지 상태를 가질 수 있다.
Qubit (quantum bit) 는 마찬가지로 0 또는 1의 두가지 상태를 가질 수 있지만, 큐비트가 0이 될 확률과 1이 될 확률로써 표현된다.
이러한 큐비트의 상태는 보통 (Psi,프사이)로 쓰며
확률진폭 , 를 사용하여 표현한다.
0이 될 확률이 , 1이 될 확률이 이다.
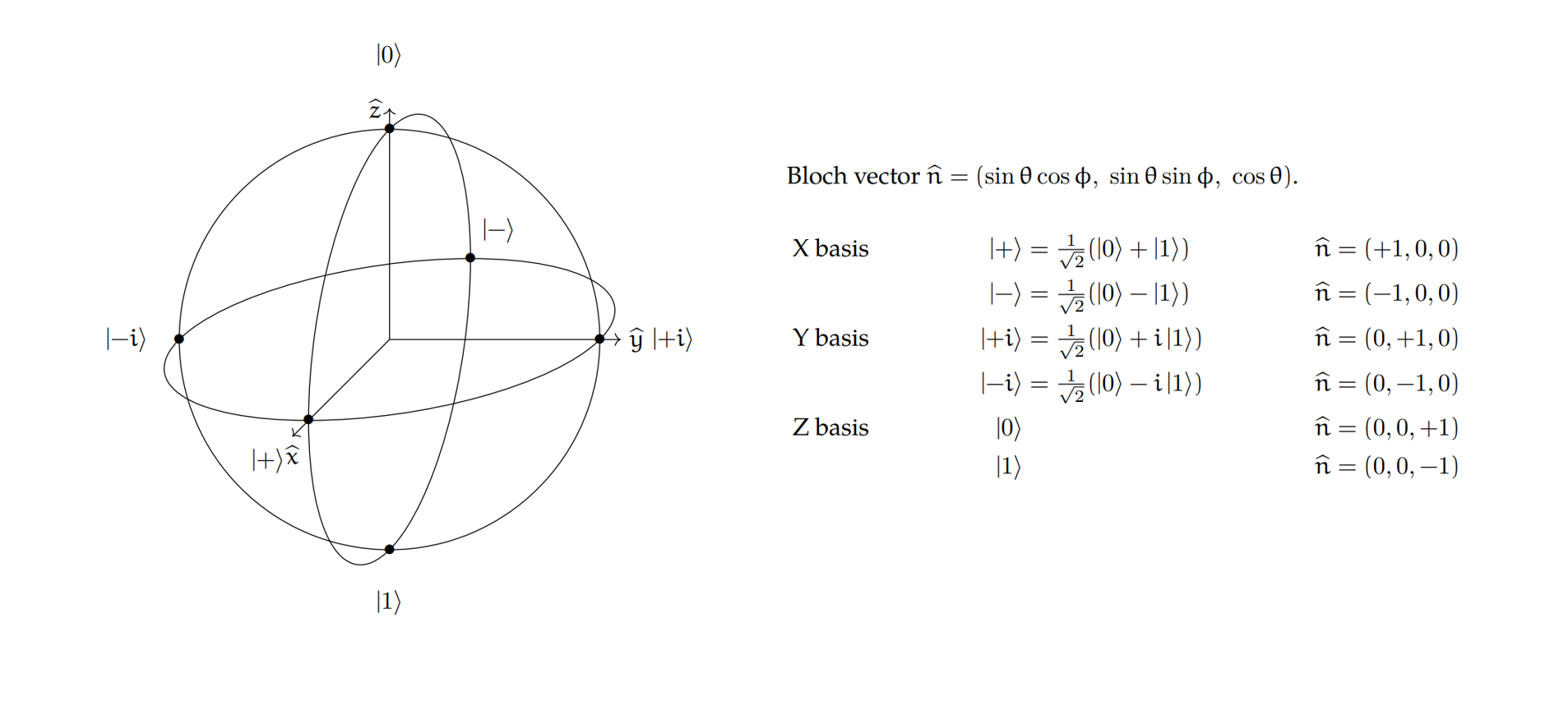
Bloch sphere 블로흐 구
블로흐구는 큐비트의 상태를 기하학적으로 표현한 것이다.
이해하기 어렵다면 데카르트 좌표계에서 x,y,z 축이 있는 것과 같다고 생각해도 된다.
0 과 1의 상태는 z축으로 표현되며, 각각의 확률이 달라짐에 따라 블로흐 구의 구면을 따라 움직인다.
예를 들어 bit는 0과 1의 값만 가질 수 있으므로 z축 위에 표현될 것이다.
1-qubit gate 단일 큐빗 게이트
고전컴퓨터에서의 단일 비트 게이트
기존의 컴퓨터에서 bit가 하나만 존재한다고하면 그것은 0또는 1의 상태를 가질 수 있다. 그래서 단일 비트 게이트도 두개 밖에 없다.
기존의 상태를 유지시키는 것(identity), 반전 시키는 것(not)
아래 사진에서 위의 게이트에 0이 들어오면 0이 출력되고, 아래 게이트에 0이 들어오면 1이 출력된다.
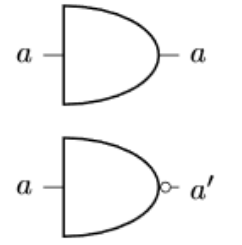
양자컴퓨터에서의 단일 큐빗 게이트
양자컴퓨터의 큐비트는 0과 1의 확률로 표현된다. 이를 0과 1이 중첩상태(super position)에 있다고 하며, 그러므로 단일 큐빗 게이트의 종류는 굉장히 많다.
우리는 먼저 ,그 중 가장 기본이 되는 pauli gate(pauli matrix)에 대해 알아보자
I gate (identity)
I 게이트는 identity이다.
즉 상태를 변화시키지 않는다.
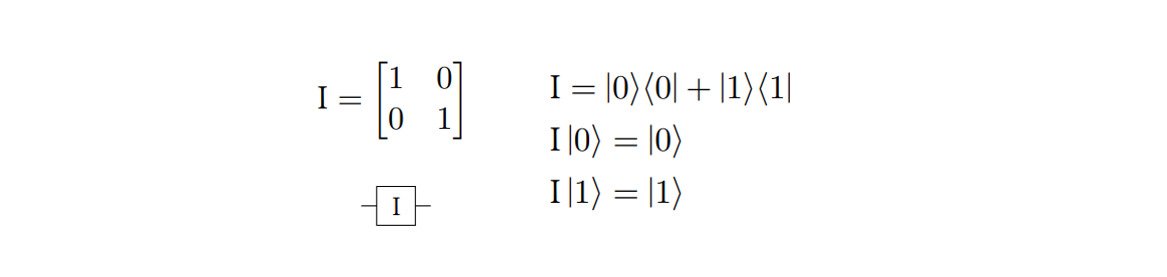
X gate
X 게이트는 not과 같은 기능을 한다.
0과 1의 상태가 바꾼다.
블로흐 구에서는 X축을 기준으로 반바퀴 돌린 것과 같다.
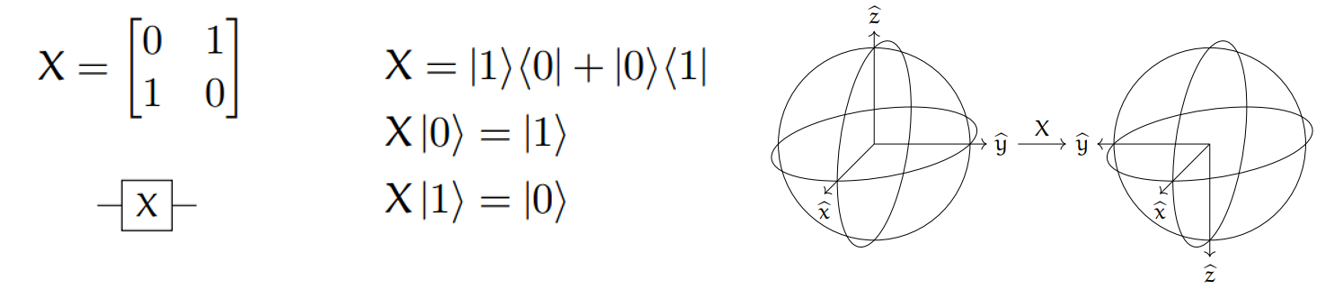
Y,Z gate
Y 게이트와 Z게이트는 아래 사진과 같다.
블로흐 구에서 각 축을 기준으로 반바퀴 돌린 것과 같다.
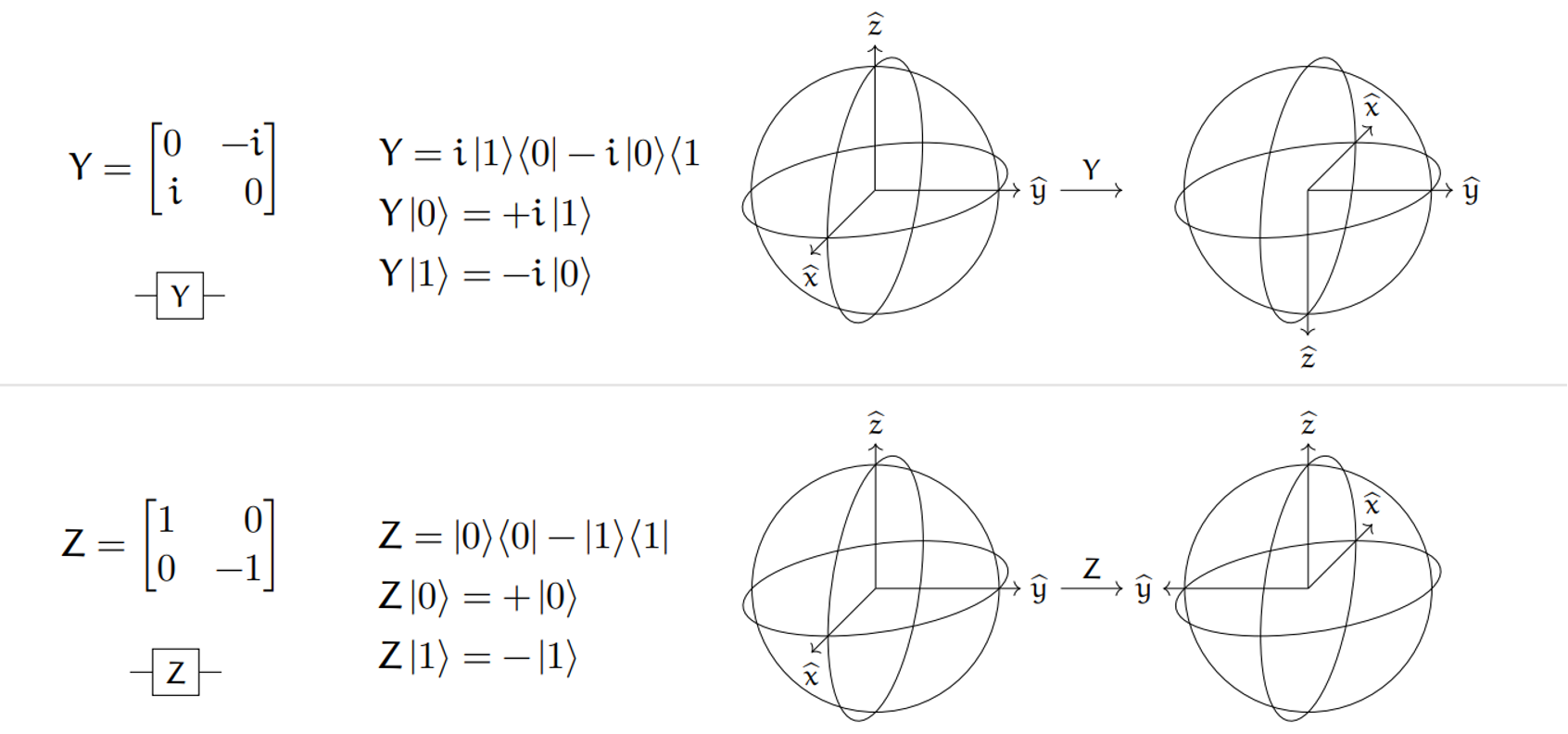
Rotation gates
로 표현되는 회전 게이트들은 각 축을 기준으로 만큼 회전 시킨다.
각 게이트는 종류가 같다면 각도를 합하여 생각해도 무방하다.
이 게이트들로 X, Y, Z 게이트를 표현할 수있는데, 예를 들어 는 x축을 기준으로 만큼 회전한 것이므로 X게이트와 같은 역할을 한다.
(Matrix의 에 를 넣어보라)
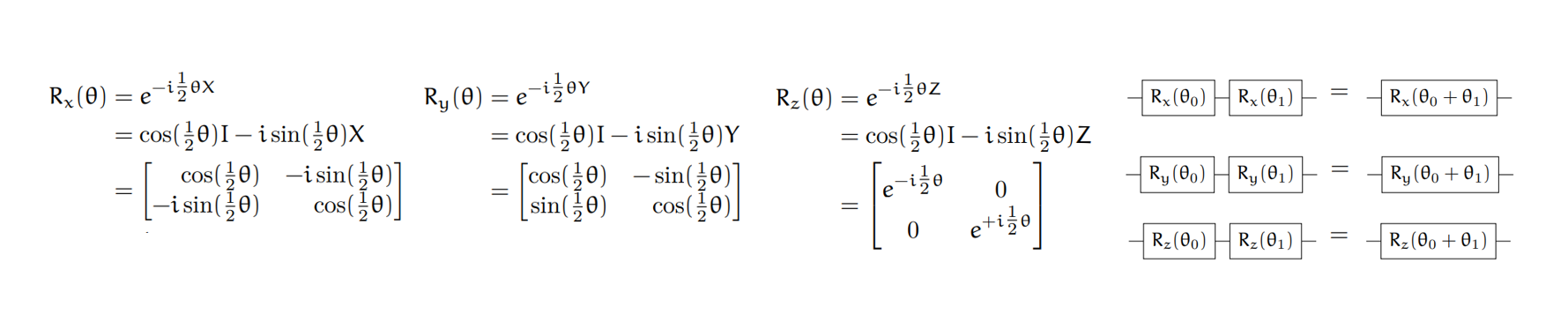
각 회전 게이트의 exp의 행렬 표현은 Taylor expansion으로 설명할 수 있다.
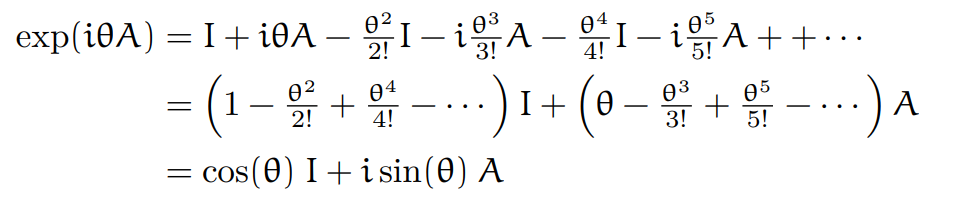
가 를 만족할 때 이다.
X, Y, Z 게이트도 제곱하면 I가 된다.
power gates
파울리 게이트 들의 t제곱들이다.
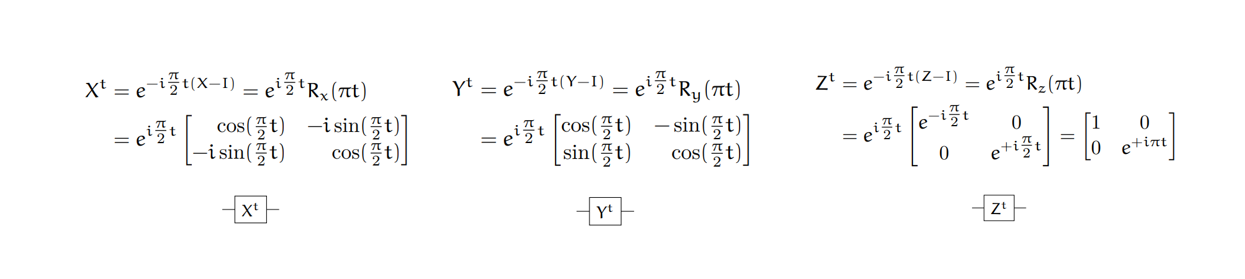
기억해 두면 좋은 power gate는
가 있다.
Hadamard gate
아다마르 게이트는 블로흐 구 상에서 인 곳을 축으로 하여 만큼 돌린 와 같다.
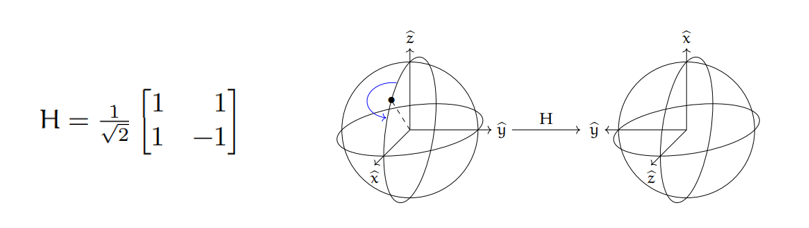
이 게이트가 특별한 이유는
0이나 1의 상태를 0과 1의 중첩 상태로 바꿔준다는 것이다.
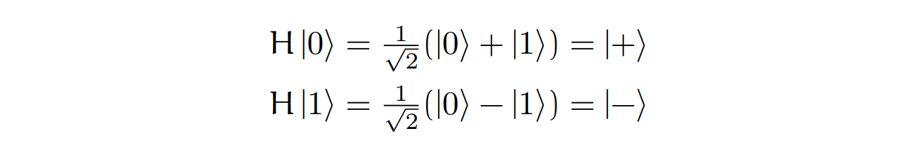
Global Phase gate
위상 게이트는 전역적인 위상을 조정한다.
이 조정은 모든 양자 상태에 동일하게 적용되며,
양자 비트 간의 상대적인 위상은 변하지 않는다.
양자 계산의 결과에 영향을 미치지 않기에 많이 사용되지는 않는다.