[F-25]Regularization,Normalization

Jake·2022년 2월 11일

AIFFEL Fundamental

Aiffel Fundamental

목록 보기

23/23

들어가며

학습 목표

정칙화(Regularization)의 개념을 이해하고 정규화(Normalization)와 구분합니다.
L1 regularization과 L2 regularization의 차이를 설명합니다.
실습을 통하여 Lp norm, Dropout, Batch Normalization에 대해 학습합니다.

Regularization과 Normalization
L1 Regularization
L2 Regularization
Extra : Lp norm
Dropout
Batch Normalization

Regularization과 Normalization

(1) Regularization? Normalization?

Regularization: 정칙화라고 불리며, 오버피팅을 해결하기 위한 방법 중 하나이다. L1,L2 Regularization, Dropout, Batch normalization 등이 있다. overfitting을 방지하기 위해 한다.

Normalization: 정규화라고 불리며, 데이터의 형태를 더 의미있게, 트레이닝에 적합하게 전처리하는 과정이다. 데이터를 z-score로 바꾸거나 minmax scaler를 사용하여 0 ~ 1 사이 값으로 분포를 조정하는 것들이 해당된다. 이들은 모든 피쳐의 범위 분포를 동일하게 해 모델이 풀어야 하는 문제를 더 간단하게 바꿔주는 전처리 과정이다.

❔ What is z-score? z-score
❕ The Z-score, or standard score, is the number of standard deviations a given data point lies above or below mean. (z = (x – μ) / σ)

from sklearn.datasets import load_iris
import pandas as pd 
import matplotlib.pyplot as plt

iris = load_iris()
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
target_df = pd.DataFrame(data=iris.target, columns=['species'])

# 0, 1, 2로 되어있는 target 데이터를 
# 알아보기 쉽게 'setosa', 'versicolor', 'virginica'로 바꿉니다 
def converter(species):
    if species == 0:
        return 'setosa'
    elif species == 1:
        return 'versicolor'
    else:
        return 'virginica'

target_df['species'] = target_df['species'].apply(converter)

iris_df = pd.concat([iris_df, target_df], axis=1)
iris_df.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

Iris data 중 virginica라는 종의 petal length(꽃잎 길이)를 X, sepal length(꽃받침의 길이)를 Y로 두고 print 해보자

X = [iris_df['petal length (cm)'][a] for a in iris_df.index if iris_df['species'][a]=='virginica']
Y = [iris_df['sepal length (cm)'][a] for a in iris_df.index if iris_df['species'][a]=='virginica']

print(X)
print(Y)

[6.0, 5.1, 5.9, 5.6, 5.8, 6.6, 4.5, 6.3, 5.8, 6.1, 5.1, 5.3, 5.5, 5.0, 5.1, 5.3, 5.5, 6.7, 6.9, 5.0, 5.7, 4.9, 6.7, 4.9, 5.7, 6.0, 4.8, 4.9, 5.6, 5.8, 6.1, 6.4, 5.6, 5.1, 5.6, 6.1, 5.6, 5.5, 4.8, 5.4, 5.6, 5.1, 5.1, 5.9, 5.7, 5.2, 5.0, 5.2, 5.4, 5.1]
[6.3, 5.8, 7.1, 6.3, 6.5, 7.6, 4.9, 7.3, 6.7, 7.2, 6.5, 6.4, 6.8, 5.7, 5.8, 6.4, 6.5, 7.7, 7.7, 6.0, 6.9, 5.6, 7.7, 6.3, 6.7, 7.2, 6.2, 6.1, 6.4, 7.2, 7.4, 7.9, 6.4, 6.3, 6.1, 7.7, 6.3, 6.4, 6.0, 6.9, 6.7, 6.9, 5.8, 6.8, 6.7, 6.7, 6.3, 6.5, 6.2, 5.9]

# 시각화-산점도
plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.title('petal-sepal scatter before normalization') 
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()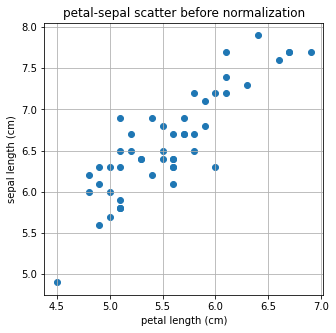

# normalization

from sklearn.preprocessing import minmax_scale

X_scale = minmax_scale(X)
Y_scale = minmax_scale(Y)

plt.figure(figsize=(5,5))
plt.scatter(X_scale,Y_scale)
plt.title('petal-sepal scatter after normalization') 
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()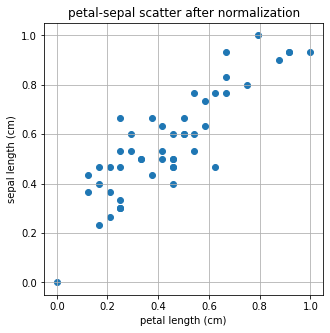

Linear Regression 모델을 사용해서 모델링해보자.Lasso와 Ridge모델도 함꼐 있으므로 이들의 차이점을 먼저 직관적으로 이해해보자.

from sklearn.linear_model import LinearRegression
import numpy as np 

X = np.array(X)
Y = np.array(Y)

# Iris Dataset을 Linear Regression으로 학습합니다. 
linear= LinearRegression()
linear.fit(X.reshape(-1,1), Y)

# Linear Regression의 기울기와 절편을 확인합니다. 
a, b=linear.coef_, linear.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))

기울기 : 1.00, 절편 : 1.06

# linear regression으로 구한 기울기, 절편으로 일차함수 그리기
plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,linear.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with linear regression') 
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()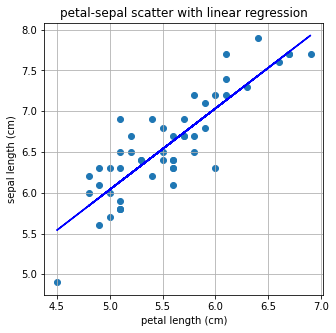

이번에는 L1, L2 Regularization으로 Regression을 해보겠습니다. 이는 Lasso, Ridge라고 부른다

# Lasoo
# L1 regularization은 Lasso로 import 합니다.
from sklearn.linear_model import Lasso

L1 = Lasso()
L1.fit(X.reshape(-1,1), Y)
a, b=L1.coef_, L1.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))

plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,L1.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with L1 regularization(Lasso)') 
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()

기울기 : 0.00, 절편 : 6.59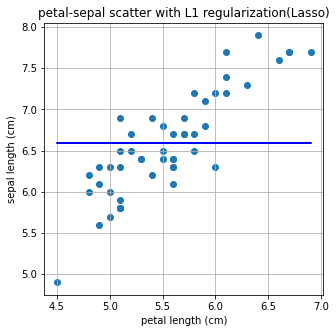

# Ridge
#L2 regularization은 Ridge로 import 합니다. 
from sklearn.linear_model import Ridge

L2 = Ridge()
L2.fit(X.reshape(-1,1), Y)
a, b = L2.coef_, L2.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))

plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,L2.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with L2 regularization(Ridge)') 
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()

기울기 : 0.93, 절편 : 1.41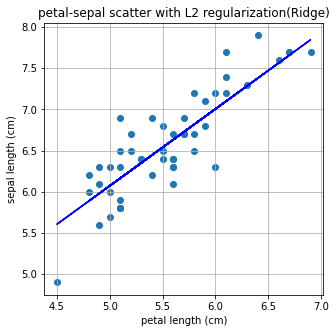

Linear Regression은 L2 Norm과 관련이 있다. 따라서 L2 Regularization을 적용한 Ridge 방법으로는 linear regression과 큰 차이가 없는 결과가 나온다.

이제, 왜 L1 Regularization을 쓰는 Lasso에서는 답이 나오지 않는지 알아보자!

L1 Regularization

(1) L1 regularization (Lasso)의 정의

L1 regularization은 아래와 같은 식으로 정의된다.

from sklearn.datasets import load_iris
import pandas as pd 
import matplotlib.pyplot as plt

iris = load_iris()
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
target_df = pd.DataFrame(data=iris.target, columns=['species'])

def converter(species):
    if species == 0:
        return 'setosa'
    elif species == 1:
        return 'versicolor'
    else:
        return 'virginica'

target_df['species'] = target_df['species'].apply(converter)

iris_df = pd.concat([iris_df, target_df], axis=1)
iris_df.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

X = [iris_df['petal length (cm)'][a] for a in iris_df.index if iris_df['species'][a]=='virginica']
Y = [iris_df['sepal length (cm)'][a] for a in iris_df.index if iris_df['species'][a]=='virginica']

X = np.array(X)
Y = np.array(Y)

plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()

from sklearn.linear_model import Lasso

L1 = Lasso()
L1.fit(X.reshape(-1,1), Y)
a, b = L1.coef_, L1.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))

plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,L1.predict(X.reshape(-1,1)),'-b')
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()

기울기 : 0.00, 절편 : 6.59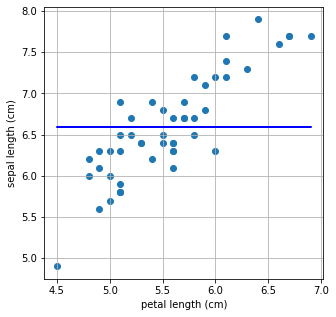

(2) 이전 스텝에서 왜 L1 Regularization 만 답이 나오지 않았을까?

(3) 컬럼 수가 많은 데이터에서의 L1 regularization 비교

Iris data는 특성이 4개로 컬럼 수가 적으니 wine dataset을 이용해보자. 총 13개의 값을 가진다.

from sklearn.datasets import load_wine

wine = load_wine()
wine_df = pd.DataFrame(data=wine.data, columns=wine.feature_names)
target_df = pd.DataFrame(data=wine.target, columns=['Y'])

#예시 
wine_df.head(5)

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline
0	14.23	1.71	2.43	15.6	127.0	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065.0
1	13.20	1.78	2.14	11.2	100.0	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050.0
2	13.16	2.36	2.67	18.6	101.0	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185.0
3	14.37	1.95	2.50	16.8	113.0	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480.0
4	13.24	2.59	2.87	21.0	118.0	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735.0

#예시
target_df.head(5)

	Y
0	0
1	0
2	0
3	0
4	0

먼저 linear regression으로 문제를 풀고, 그 계수와 MAE, MSE, RMSE를 출력해보자.

# linear regression

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

# 데이터를 준비하고
X_train, X_test, y_train, y_test = train_test_split(wine_df, target_df, test_size=0.3, random_state=101)

# 모델을 훈련시킵니다.
model = LinearRegression()
model.fit(X_train, y_train)

# 테스트를 해볼까요?
model.predict(X_test)
pred = model.predict(X_test)

# 테스트 결과는 이렇습니다!
print("result of linear regression")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient linear regression")
print(model.coef_)

result of linear regression
Mean Absolute Error: 0.25128973939722626
Mean Squared Error: 0.1062458740952556
Mean Root Squared Error: 0.32595379134971814


 coefficient linear regression
[[-8.09017190e-02  4.34817880e-02 -1.18857931e-01  3.65705449e-02
  -4.68014203e-04  1.41423581e-01 -4.54107854e-01 -5.13172664e-01
   9.69318443e-02  5.34311136e-02 -1.27626604e-01 -2.91381844e-01
  -5.72238959e-04]]

# L1 legularization으로 문제를 풀어보자.
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_absolute_error, mean_squared_error

# 모델을 준비하고 훈련시킵니다.
L1 = Lasso(alpha=0.05)
L1.fit(X_train, y_train)

# 테스트를 해봅시다.
pred = L1.predict(X_test)

# 모델 성능은 얼마나 좋을까요?
print("result of Lasso")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient of Lasso")
print(L1.coef_)

result of Lasso
Mean Absolute Error: 0.24233731936122138
Mean Squared Error: 0.0955956894578189
Mean Root Squared Error: 0.3091855259513597


 coefficient of Lasso
[-0.          0.01373795 -0.          0.03065716  0.00154719 -0.
 -0.34143614 -0.          0.          0.06755943 -0.         -0.14558153
 -0.00089635]

결과분석

coefficient부분을 보면 Linear regression과 lasso 차이가 더 두드러짐을 알 수 있다. linear regression에서는 모든 칼럼의 가중치를 탐색해 구하는 반면, L1 regularization에서는 총 13개 중 7개를 제외한 값들이 모두 0임을 알 수 있다.

Error부분에서는 큰 차이가 없었지만, 어떤 컬럼이 결과에 영향을 크게 미치는지 확실히 확인할 수 있다. 이 경우 다른 문제에서도 error 차이가 크지 않다면, ㅊ차원 축소와 비슷한 개념으로 변수값을 7개만 남겨도 충분히 결과를 예측할 것이다.

다만 linear regression과 L1, L2 Regularization의 차이 중 하나는 $\alpha$ 라는 하이퍼파라미터가 하나 더 들어간다는 것이고, 그 값에 따라 error에 영향을 미친다는 것이다.

L2 Regularization

(1) L2 Regularization(Ridge) 의 정의

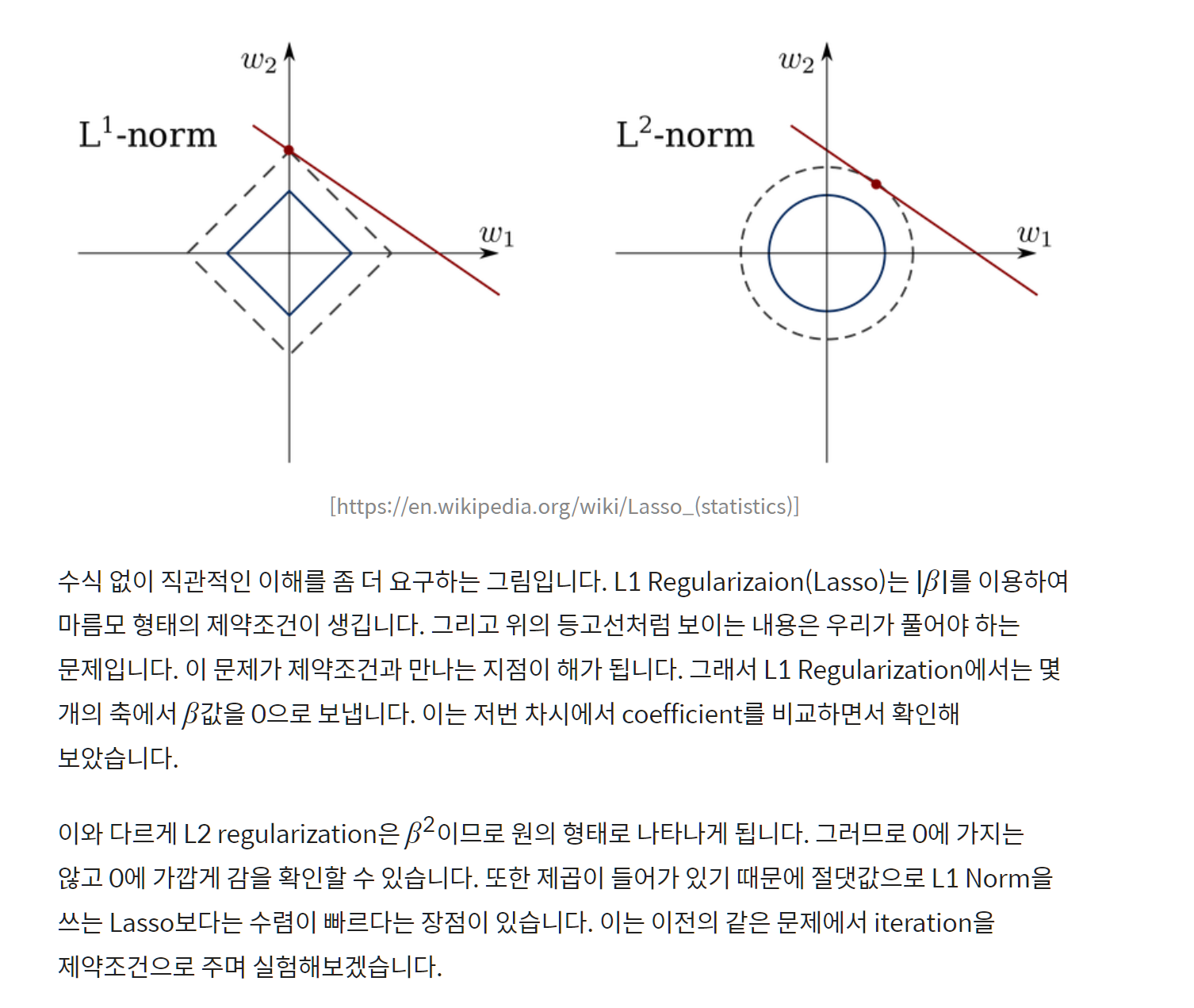
(2) L1 vs L2 Regularization

from sklearn.datasets import load_wine
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error

wine = load_wine()
wine_df = pd.DataFrame(data=wine.data, columns=wine.feature_names)
target_df = pd.DataFrame(data=wine.target, columns=['Y'])
X_train, X_test, y_train, y_test = train_test_split(wine_df, target_df, test_size= 0.3, random_state=101)
print('=3')

=3

# L1 regularization으로 iter=5로 두고 풀어보기
from sklearn.linear_model import Lasso

L1 = Lasso(alpha=0.05, max_iter=5)
L1.fit(X_train, y_train)
pred = L1.predict(X_test)

print("result of Lasso")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient of Lasso")
print(L1.coef_)

result of Lasso
Mean Absolute Error: 0.24845768841769436
Mean Squared Error: 0.10262989110341268
Mean Root Squared Error: 0.32035900346862844


 coefficient of Lasso
[-0.          0.         -0.          0.03295564  0.00109495  0.
 -0.4027847   0.          0.          0.06023131 -0.         -0.12001119
 -0.00078971]


/opt/conda/lib/python3.9/site-packages/sklearn/linear_model/_coordinate_descent.py:645: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations, check the scale of the features or consider increasing regularisation. Duality gap: 3.924e+00, tolerance: 7.480e-03
  model = cd_fast.enet_coordinate_descent(

# L2 동일한 제약 조건으로.
from sklearn.linear_model import Ridge

L2 = Ridge(alpha=0.05,max_iter=5)
L2.fit(X_train, y_train)
pred = L2.predict(X_test)

print("result of Ridge")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient of Ridge")
print(L2.coef_)

result of Ridge
Mean Absolute Error: 0.251146695993643
Mean Squared Error: 0.10568076460795564
Mean Root Squared Error: 0.3250857803841251


 coefficient of Ridge
[[-8.12456257e-02  4.35541496e-02 -1.21661565e-01  3.65979773e-02
  -3.94014013e-04  1.39168707e-01 -4.50691113e-01 -4.87216747e-01
   9.54111059e-02  5.37077039e-02 -1.28602933e-01 -2.89832790e-01
  -5.73136185e-04]]

L1 Regularization은 가중치가 적은 벡터에 해당하는 계수를 0으로 보내면서 차원 축소와 비슷한 역할을 하는 것이 특징이며, L2 Regularization은 0이 아닌 0에 가깝게 보내지만 제곱 텀이 있기 때문에 L1 보다 수렴속도가 빠르다는 장점이 있다.

데이터에 따라 적절한 Regularization 방법을 활용하는 것이 좋다.

Extra: Lp norm

(1) vector norm

x=np.array([1,10,1,1,1])
p=2
norm_x=np.linalg.norm(x, ord=p)
making_norm = (sum(x**p))**(1/p)
print("result of numpy package norm function : %0.5f "%norm_x) 
print("result of making norm : %0.5f "%making_norm)

result of numpy package norm function : 10.19804 
result of making norm : 10.19804

p가 우리가 생각하는 자연수가 아닌 경우 어떻게 될까?

p = ∞ Infinity norm의 경우는 가장 큰 숫자를 출력한다.

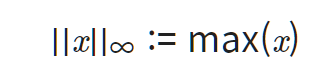
norm_x=np.linalg.norm(x, ord=np.inf)
print("result of infinite norm : %0.5f "%norm_x)

result of infinite norm : 10.00000

(2) matrix norm

A=np.array([[1,2,3],[1,2,3],[4,6,8]])
inf_norm_A=np.linalg.norm(A, ord=np.inf)
print("result inf norm of A :", inf_norm_A)
one_norm_A=np.linalg.norm(A, ord=1)
print("result one norm of A :", one_norm_A)

result inf norm of A : 18.0
result one norm of A : 14.0

Dropout

논문 제목 : Dropout: A Simple Way to Prevent Neural Networks from Overfitting
논문 발표 시점 : 2014년
논문 링크 : 논문 주소(https://jmlr.org/papers/v15/srivastava14a.html)
참고 영상

Dropout은 오버피팅을 막는 Regularization layer 중 하나이다. fully connected layer에서 오버피팅이 생기는 경우에 주로 Dropout layer를 추가한다.

(1) 실습: not overfitting

Fashion MNIST datset으로 학습을 시키자. 드롭아웃 레이어를 확률을 1에 가깝게 주면 어떻게 되는지 살펴보자.

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

fashion_mnist = keras.datasets.fashion_mnist
print('=3')

=3

(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
               'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

train_images = train_images / 255.0
test_images = test_images / 255.0

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
32768/29515 [=================================] - 0s 0us/step
40960/29515 [=========================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26427392/26421880 [==============================] - 0s 0us/step
26435584/26421880 [==============================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
16384/5148 [===============================================================================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 0s 0us/step
4431872/4422102 [==============================] - 0s 0us/step

dropout 확률을 0.9로 주었을 때의 결과를 살펴보자.

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation='relu'),
    # 여기에 dropout layer를 추가해보았습니다. 나머지 layer는 아래의 실습과 같습니다.
    keras.layers.Dropout(0.9),
    keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history= model.fit(train_images, train_labels, epochs=5)

Epoch 1/5
1875/1875 [==============================] - 3s 2ms/step - loss: 1.3670 - accuracy: 0.4603
Epoch 2/5
1875/1875 [==============================] - 3s 2ms/step - loss: 1.1633 - accuracy: 0.5303
Epoch 3/5
1875/1875 [==============================] - 3s 2ms/step - loss: 1.1038 - accuracy: 0.5543
Epoch 4/5
1875/1875 [==============================] - 3s 2ms/step - loss: 1.0815 - accuracy: 0.5630
Epoch 5/5
1875/1875 [==============================] - 3s 2ms/step - loss: 1.0603 - accuracy: 0.5733

dropout이 없을 때 실습을 하면, 5 epoch만 돌려도 높은 정확도를 볼 수 있다.

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    # 이번에는 dropout layer가 없습니다. 
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history = model.fit(train_images, train_labels, epochs=5)

Epoch 1/5
1875/1875 [==============================] - 11s 2ms/step - loss: 0.4982 - accuracy: 0.8240
Epoch 2/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.3765 - accuracy: 0.8639
Epoch 3/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.3370 - accuracy: 0.8775
Epoch 4/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.3138 - accuracy: 0.8847
Epoch 5/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.2952 - accuracy: 0.8913

(2) 실습: overfitting

일부러 overfitting을 시켜보기 위해 train set을 99%로 늘리고 validation set을 줄여보자.

X_train, X_valid, y_train, y_valid = train_test_split(train_images, train_labels, test_size=0.01, random_state=101)
X_train = X_train / 255.0
X_valid = X_valid / 255.0

#Dense layer만으로 만들어 낸 classification 모델입니다.
model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(256, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history= model.fit(X_train, y_train, epochs=200, batch_size=512, validation_data=(X_valid, y_valid))

Epoch 1/200
117/117 [==============================] - 1s 4ms/step - loss: 2.0525 - accuracy: 0.5124 - val_loss: 1.6445 - val_accuracy: 0.5867
Epoch 2/200
117/117 [==============================] - 0s 2ms/step - loss: 1.4014 - accuracy: 0.6157 - val_loss: 1.1777 - val_accuracy: 0.6717
Epoch 3/200
117/117 [==============================] - 0s 2ms/step - loss: 1.0744 - accuracy: 0.6819 - val_loss: 0.9525 - val_accuracy: 0.7383
Epoch 4/200
117/117 [==============================] - 0s 2ms/step - loss: 0.8927 - accuracy: 0.7204 - val_loss: 0.8173 - val_accuracy: 0.7517
Epoch 5/200
117/117 [==============================] - 0s 3ms/step - loss: 0.7859 - accuracy: 0.7377 - val_loss: 0.7317 - val_accuracy: 0.7717
Epoch 6/200
117/117 [==============================] - 0s 3ms/step - loss: 0.7204 - accuracy: 0.7495 - val_loss: 0.6817 - val_accuracy: 0.7750
Epoch 7/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6774 - accuracy: 0.7602 - val_loss: 0.6500 - val_accuracy: 0.7867
Epoch 8/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6458 - accuracy: 0.7685 - val_loss: 0.6219 - val_accuracy: 0.7967
Epoch 9/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6207 - accuracy: 0.7779 - val_loss: 0.6015 - val_accuracy: 0.7883
Epoch 10/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6019 - accuracy: 0.7831 - val_loss: 0.5808 - val_accuracy: 0.7933
Epoch 11/200
117/117 [==============================] - 0s 2ms/step - loss: 0.5833 - accuracy: 0.7918 - val_loss: 0.5681 - val_accuracy: 0.7933
Epoch 12/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5675 - accuracy: 0.7988 - val_loss: 0.5545 - val_accuracy: 0.8033
Epoch 13/200
117/117 [==============================] - 0s 2ms/step - loss: 0.5540 - accuracy: 0.8043 - val_loss: 0.5454 - val_accuracy: 0.7983
Epoch 14/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5422 - accuracy: 0.8093 - val_loss: 0.5364 - val_accuracy: 0.8033
Epoch 15/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5311 - accuracy: 0.8129 - val_loss: 0.5224 - val_accuracy: 0.8083
Epoch 16/200
117/117 [==============================] - 0s 2ms/step - loss: 0.5212 - accuracy: 0.8171 - val_loss: 0.5176 - val_accuracy: 0.8117
Epoch 17/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5124 - accuracy: 0.8207 - val_loss: 0.5103 - val_accuracy: 0.8100
Epoch 18/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5041 - accuracy: 0.8245 - val_loss: 0.5037 - val_accuracy: 0.8150
Epoch 19/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4972 - accuracy: 0.8250 - val_loss: 0.4983 - val_accuracy: 0.8183
Epoch 20/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4901 - accuracy: 0.8275 - val_loss: 0.4894 - val_accuracy: 0.8167
Epoch 21/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4853 - accuracy: 0.8295 - val_loss: 0.4872 - val_accuracy: 0.8217
Epoch 22/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4789 - accuracy: 0.8325 - val_loss: 0.4819 - val_accuracy: 0.8183
Epoch 23/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4731 - accuracy: 0.8343 - val_loss: 0.4753 - val_accuracy: 0.8283
Epoch 24/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4683 - accuracy: 0.8368 - val_loss: 0.4696 - val_accuracy: 0.8250
Epoch 25/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4634 - accuracy: 0.8376 - val_loss: 0.4660 - val_accuracy: 0.8217
Epoch 26/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4597 - accuracy: 0.8393 - val_loss: 0.4623 - val_accuracy: 0.8250
Epoch 27/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4557 - accuracy: 0.8412 - val_loss: 0.4558 - val_accuracy: 0.8267
Epoch 28/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4519 - accuracy: 0.8414 - val_loss: 0.4524 - val_accuracy: 0.8283
Epoch 29/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4485 - accuracy: 0.8438 - val_loss: 0.4566 - val_accuracy: 0.8267
Epoch 30/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4471 - accuracy: 0.8432 - val_loss: 0.4479 - val_accuracy: 0.8367
Epoch 31/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4419 - accuracy: 0.8451 - val_loss: 0.4419 - val_accuracy: 0.8317
Epoch 32/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4394 - accuracy: 0.8465 - val_loss: 0.4381 - val_accuracy: 0.8300
Epoch 33/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4366 - accuracy: 0.8469 - val_loss: 0.4394 - val_accuracy: 0.8317
Epoch 34/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4331 - accuracy: 0.8487 - val_loss: 0.4361 - val_accuracy: 0.8317
Epoch 35/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4305 - accuracy: 0.8492 - val_loss: 0.4340 - val_accuracy: 0.8317
Epoch 36/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4283 - accuracy: 0.8502 - val_loss: 0.4339 - val_accuracy: 0.8350
Epoch 37/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4261 - accuracy: 0.8500 - val_loss: 0.4307 - val_accuracy: 0.8350
Epoch 38/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4237 - accuracy: 0.8520 - val_loss: 0.4275 - val_accuracy: 0.8350
Epoch 39/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4214 - accuracy: 0.8527 - val_loss: 0.4246 - val_accuracy: 0.8367
Epoch 40/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4193 - accuracy: 0.8531 - val_loss: 0.4250 - val_accuracy: 0.8400
Epoch 41/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4175 - accuracy: 0.8539 - val_loss: 0.4224 - val_accuracy: 0.8317
Epoch 42/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4147 - accuracy: 0.8542 - val_loss: 0.4187 - val_accuracy: 0.8433
Epoch 43/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4139 - accuracy: 0.8552 - val_loss: 0.4183 - val_accuracy: 0.8400
Epoch 44/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4115 - accuracy: 0.8557 - val_loss: 0.4150 - val_accuracy: 0.8367
Epoch 45/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4087 - accuracy: 0.8570 - val_loss: 0.4201 - val_accuracy: 0.8350
Epoch 46/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4079 - accuracy: 0.8571 - val_loss: 0.4220 - val_accuracy: 0.8300
Epoch 47/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4076 - accuracy: 0.8577 - val_loss: 0.4117 - val_accuracy: 0.8383
Epoch 48/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4031 - accuracy: 0.8588 - val_loss: 0.4105 - val_accuracy: 0.8333
Epoch 49/200
117/117 [==============================] - 0s 2ms/step - loss: 0.4021 - accuracy: 0.8585 - val_loss: 0.4085 - val_accuracy: 0.8367
Epoch 50/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4007 - accuracy: 0.8591 - val_loss: 0.4077 - val_accuracy: 0.8333
Epoch 51/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3985 - accuracy: 0.8605 - val_loss: 0.4048 - val_accuracy: 0.8367
Epoch 52/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3972 - accuracy: 0.8606 - val_loss: 0.4037 - val_accuracy: 0.8367
Epoch 53/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3963 - accuracy: 0.8604 - val_loss: 0.4010 - val_accuracy: 0.8367
Epoch 54/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3938 - accuracy: 0.8621 - val_loss: 0.4022 - val_accuracy: 0.8333
Epoch 55/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3928 - accuracy: 0.8626 - val_loss: 0.4008 - val_accuracy: 0.8317
Epoch 56/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3918 - accuracy: 0.8626 - val_loss: 0.3986 - val_accuracy: 0.8400
Epoch 57/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3897 - accuracy: 0.8635 - val_loss: 0.4002 - val_accuracy: 0.8350
Epoch 58/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3886 - accuracy: 0.8637 - val_loss: 0.3951 - val_accuracy: 0.8350
Epoch 59/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3878 - accuracy: 0.8641 - val_loss: 0.3931 - val_accuracy: 0.8350
Epoch 60/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3853 - accuracy: 0.8649 - val_loss: 0.3955 - val_accuracy: 0.8417
Epoch 61/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3846 - accuracy: 0.8651 - val_loss: 0.3919 - val_accuracy: 0.8450
Epoch 62/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3827 - accuracy: 0.8659 - val_loss: 0.3939 - val_accuracy: 0.8383
Epoch 63/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3823 - accuracy: 0.8661 - val_loss: 0.3895 - val_accuracy: 0.8400
Epoch 64/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3803 - accuracy: 0.8659 - val_loss: 0.3921 - val_accuracy: 0.8383
Epoch 65/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3803 - accuracy: 0.8667 - val_loss: 0.3912 - val_accuracy: 0.8400
Epoch 66/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3779 - accuracy: 0.8672 - val_loss: 0.3874 - val_accuracy: 0.8467
Epoch 67/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3775 - accuracy: 0.8666 - val_loss: 0.3900 - val_accuracy: 0.8417
Epoch 68/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3760 - accuracy: 0.8678 - val_loss: 0.3869 - val_accuracy: 0.8483
Epoch 69/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3763 - accuracy: 0.8672 - val_loss: 0.3865 - val_accuracy: 0.8483
Epoch 70/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3732 - accuracy: 0.8689 - val_loss: 0.3796 - val_accuracy: 0.8417
Epoch 71/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3725 - accuracy: 0.8696 - val_loss: 0.3858 - val_accuracy: 0.8517
Epoch 72/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3716 - accuracy: 0.8694 - val_loss: 0.3800 - val_accuracy: 0.8500
Epoch 73/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3710 - accuracy: 0.8697 - val_loss: 0.3782 - val_accuracy: 0.8467
Epoch 74/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3695 - accuracy: 0.8700 - val_loss: 0.3753 - val_accuracy: 0.8500
Epoch 75/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3698 - accuracy: 0.8700 - val_loss: 0.3830 - val_accuracy: 0.8517
Epoch 76/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3670 - accuracy: 0.8707 - val_loss: 0.3740 - val_accuracy: 0.8433
Epoch 77/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3670 - accuracy: 0.8708 - val_loss: 0.3758 - val_accuracy: 0.8433
Epoch 78/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3654 - accuracy: 0.8716 - val_loss: 0.3768 - val_accuracy: 0.8383
Epoch 79/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3637 - accuracy: 0.8722 - val_loss: 0.3711 - val_accuracy: 0.8500
Epoch 80/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3626 - accuracy: 0.8724 - val_loss: 0.3753 - val_accuracy: 0.8467
Epoch 81/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3622 - accuracy: 0.8724 - val_loss: 0.3695 - val_accuracy: 0.8500
Epoch 82/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3610 - accuracy: 0.8734 - val_loss: 0.3722 - val_accuracy: 0.8433
Epoch 83/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3607 - accuracy: 0.8732 - val_loss: 0.3714 - val_accuracy: 0.8433
Epoch 84/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3598 - accuracy: 0.8740 - val_loss: 0.3703 - val_accuracy: 0.8467
Epoch 85/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3587 - accuracy: 0.8739 - val_loss: 0.3679 - val_accuracy: 0.8500
Epoch 86/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3569 - accuracy: 0.8745 - val_loss: 0.3702 - val_accuracy: 0.8550
Epoch 87/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3564 - accuracy: 0.8754 - val_loss: 0.3694 - val_accuracy: 0.8500
Epoch 88/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3558 - accuracy: 0.8745 - val_loss: 0.3679 - val_accuracy: 0.8567
Epoch 89/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3549 - accuracy: 0.8751 - val_loss: 0.3722 - val_accuracy: 0.8550
Epoch 90/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3541 - accuracy: 0.8756 - val_loss: 0.3668 - val_accuracy: 0.8567
Epoch 91/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3535 - accuracy: 0.8758 - val_loss: 0.3647 - val_accuracy: 0.8533
Epoch 92/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3517 - accuracy: 0.8771 - val_loss: 0.3666 - val_accuracy: 0.8517
Epoch 93/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3506 - accuracy: 0.8766 - val_loss: 0.3634 - val_accuracy: 0.8500
Epoch 94/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3500 - accuracy: 0.8767 - val_loss: 0.3646 - val_accuracy: 0.8550
Epoch 95/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3502 - accuracy: 0.8760 - val_loss: 0.3659 - val_accuracy: 0.8617
Epoch 96/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3486 - accuracy: 0.8771 - val_loss: 0.3614 - val_accuracy: 0.8533
Epoch 97/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3469 - accuracy: 0.8782 - val_loss: 0.3605 - val_accuracy: 0.8517
Epoch 98/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3464 - accuracy: 0.8781 - val_loss: 0.3620 - val_accuracy: 0.8600
Epoch 99/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3457 - accuracy: 0.8778 - val_loss: 0.3623 - val_accuracy: 0.8517
Epoch 100/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3448 - accuracy: 0.8783 - val_loss: 0.3584 - val_accuracy: 0.8483
Epoch 101/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3443 - accuracy: 0.8786 - val_loss: 0.3593 - val_accuracy: 0.8550
Epoch 102/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3430 - accuracy: 0.8793 - val_loss: 0.3608 - val_accuracy: 0.8533
Epoch 103/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3424 - accuracy: 0.8797 - val_loss: 0.3584 - val_accuracy: 0.8500
Epoch 104/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3415 - accuracy: 0.8794 - val_loss: 0.3539 - val_accuracy: 0.8533
Epoch 105/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3401 - accuracy: 0.8799 - val_loss: 0.3596 - val_accuracy: 0.8600
Epoch 106/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3400 - accuracy: 0.8796 - val_loss: 0.3641 - val_accuracy: 0.8517
Epoch 107/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3396 - accuracy: 0.8800 - val_loss: 0.3593 - val_accuracy: 0.8567
Epoch 108/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3381 - accuracy: 0.8811 - val_loss: 0.3688 - val_accuracy: 0.8567
Epoch 109/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3389 - accuracy: 0.8799 - val_loss: 0.3559 - val_accuracy: 0.8533
Epoch 110/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3365 - accuracy: 0.8812 - val_loss: 0.3512 - val_accuracy: 0.8533
Epoch 111/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3366 - accuracy: 0.8808 - val_loss: 0.3528 - val_accuracy: 0.8517
Epoch 112/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3358 - accuracy: 0.8811 - val_loss: 0.3537 - val_accuracy: 0.8517
Epoch 113/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3340 - accuracy: 0.8820 - val_loss: 0.3528 - val_accuracy: 0.8500
Epoch 114/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3331 - accuracy: 0.8826 - val_loss: 0.3526 - val_accuracy: 0.8550
Epoch 115/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3324 - accuracy: 0.8827 - val_loss: 0.3548 - val_accuracy: 0.8567
Epoch 116/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3316 - accuracy: 0.8838 - val_loss: 0.3491 - val_accuracy: 0.8450
Epoch 117/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3311 - accuracy: 0.8829 - val_loss: 0.3541 - val_accuracy: 0.8550
Epoch 118/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3305 - accuracy: 0.8835 - val_loss: 0.3472 - val_accuracy: 0.8500
Epoch 119/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3300 - accuracy: 0.8830 - val_loss: 0.3506 - val_accuracy: 0.8533
Epoch 120/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3288 - accuracy: 0.8839 - val_loss: 0.3499 - val_accuracy: 0.8550
Epoch 121/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3286 - accuracy: 0.8831 - val_loss: 0.3492 - val_accuracy: 0.8550
Epoch 122/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3268 - accuracy: 0.8844 - val_loss: 0.3494 - val_accuracy: 0.8517
Epoch 123/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3264 - accuracy: 0.8851 - val_loss: 0.3477 - val_accuracy: 0.8533
Epoch 124/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3261 - accuracy: 0.8842 - val_loss: 0.3489 - val_accuracy: 0.8633
Epoch 125/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3260 - accuracy: 0.8849 - val_loss: 0.3441 - val_accuracy: 0.8517
Epoch 126/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3238 - accuracy: 0.8852 - val_loss: 0.3482 - val_accuracy: 0.8617
Epoch 127/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3238 - accuracy: 0.8855 - val_loss: 0.3471 - val_accuracy: 0.8583
Epoch 128/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3239 - accuracy: 0.8858 - val_loss: 0.3477 - val_accuracy: 0.8533
Epoch 129/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3231 - accuracy: 0.8851 - val_loss: 0.3450 - val_accuracy: 0.8650
Epoch 130/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3229 - accuracy: 0.8854 - val_loss: 0.3469 - val_accuracy: 0.8600
Epoch 131/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3226 - accuracy: 0.8853 - val_loss: 0.3445 - val_accuracy: 0.8567
Epoch 132/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3204 - accuracy: 0.8857 - val_loss: 0.3480 - val_accuracy: 0.8583
Epoch 133/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3191 - accuracy: 0.8865 - val_loss: 0.3426 - val_accuracy: 0.8567
Epoch 134/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3186 - accuracy: 0.8873 - val_loss: 0.3441 - val_accuracy: 0.8617
Epoch 135/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3181 - accuracy: 0.8878 - val_loss: 0.3452 - val_accuracy: 0.8600
Epoch 136/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3179 - accuracy: 0.8872 - val_loss: 0.3438 - val_accuracy: 0.8600
Epoch 137/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3173 - accuracy: 0.8874 - val_loss: 0.3449 - val_accuracy: 0.8633
Epoch 138/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3160 - accuracy: 0.8881 - val_loss: 0.3431 - val_accuracy: 0.8600
Epoch 139/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3150 - accuracy: 0.8879 - val_loss: 0.3407 - val_accuracy: 0.8700
Epoch 140/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3156 - accuracy: 0.8883 - val_loss: 0.3516 - val_accuracy: 0.8600
Epoch 141/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3152 - accuracy: 0.8885 - val_loss: 0.3443 - val_accuracy: 0.8600
Epoch 142/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3140 - accuracy: 0.8880 - val_loss: 0.3401 - val_accuracy: 0.8633
Epoch 143/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3129 - accuracy: 0.8890 - val_loss: 0.3482 - val_accuracy: 0.8600
Epoch 144/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3160 - accuracy: 0.8870 - val_loss: 0.3423 - val_accuracy: 0.8583
Epoch 145/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3117 - accuracy: 0.8890 - val_loss: 0.3416 - val_accuracy: 0.8650
Epoch 146/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3114 - accuracy: 0.8895 - val_loss: 0.3393 - val_accuracy: 0.8650
Epoch 147/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3099 - accuracy: 0.8895 - val_loss: 0.3383 - val_accuracy: 0.8617
Epoch 148/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3107 - accuracy: 0.8894 - val_loss: 0.3456 - val_accuracy: 0.8583
Epoch 149/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3104 - accuracy: 0.8897 - val_loss: 0.3439 - val_accuracy: 0.8683
Epoch 150/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3092 - accuracy: 0.8909 - val_loss: 0.3351 - val_accuracy: 0.8700
Epoch 151/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3088 - accuracy: 0.8897 - val_loss: 0.3374 - val_accuracy: 0.8683
Epoch 152/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3078 - accuracy: 0.8899 - val_loss: 0.3422 - val_accuracy: 0.8500
Epoch 153/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3083 - accuracy: 0.8903 - val_loss: 0.3407 - val_accuracy: 0.8667
Epoch 154/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3064 - accuracy: 0.8911 - val_loss: 0.3356 - val_accuracy: 0.8633
Epoch 155/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3062 - accuracy: 0.8913 - val_loss: 0.3325 - val_accuracy: 0.8717
Epoch 156/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3053 - accuracy: 0.8919 - val_loss: 0.3379 - val_accuracy: 0.8683
Epoch 157/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3055 - accuracy: 0.8907 - val_loss: 0.3354 - val_accuracy: 0.8617
Epoch 158/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3038 - accuracy: 0.8913 - val_loss: 0.3320 - val_accuracy: 0.8667
Epoch 159/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3047 - accuracy: 0.8912 - val_loss: 0.3394 - val_accuracy: 0.8633
Epoch 160/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3032 - accuracy: 0.8920 - val_loss: 0.3370 - val_accuracy: 0.8667
Epoch 161/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3022 - accuracy: 0.8925 - val_loss: 0.3366 - val_accuracy: 0.8733
Epoch 162/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3017 - accuracy: 0.8926 - val_loss: 0.3362 - val_accuracy: 0.8633
Epoch 163/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3022 - accuracy: 0.8919 - val_loss: 0.3353 - val_accuracy: 0.8650
Epoch 164/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3010 - accuracy: 0.8929 - val_loss: 0.3281 - val_accuracy: 0.8683
Epoch 165/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3008 - accuracy: 0.8929 - val_loss: 0.3377 - val_accuracy: 0.8733
Epoch 166/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3007 - accuracy: 0.8931 - val_loss: 0.3384 - val_accuracy: 0.8650
Epoch 167/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2995 - accuracy: 0.8924 - val_loss: 0.3311 - val_accuracy: 0.8733
Epoch 168/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2991 - accuracy: 0.8931 - val_loss: 0.3348 - val_accuracy: 0.8633
Epoch 169/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2991 - accuracy: 0.8949 - val_loss: 0.3337 - val_accuracy: 0.8683
Epoch 170/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2977 - accuracy: 0.8939 - val_loss: 0.3324 - val_accuracy: 0.8733
Epoch 171/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2975 - accuracy: 0.8943 - val_loss: 0.3323 - val_accuracy: 0.8700
Epoch 172/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2966 - accuracy: 0.8941 - val_loss: 0.3317 - val_accuracy: 0.8700
Epoch 173/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2980 - accuracy: 0.8939 - val_loss: 0.3293 - val_accuracy: 0.8750
Epoch 174/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2952 - accuracy: 0.8954 - val_loss: 0.3304 - val_accuracy: 0.8733
Epoch 175/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2949 - accuracy: 0.8949 - val_loss: 0.3361 - val_accuracy: 0.8617
Epoch 176/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2942 - accuracy: 0.8951 - val_loss: 0.3329 - val_accuracy: 0.8650
Epoch 177/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2943 - accuracy: 0.8951 - val_loss: 0.3286 - val_accuracy: 0.8650
Epoch 178/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2932 - accuracy: 0.8955 - val_loss: 0.3326 - val_accuracy: 0.8717
Epoch 179/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2933 - accuracy: 0.8957 - val_loss: 0.3305 - val_accuracy: 0.8650
Epoch 180/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2926 - accuracy: 0.8958 - val_loss: 0.3255 - val_accuracy: 0.8700
Epoch 181/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2947 - accuracy: 0.8952 - val_loss: 0.3314 - val_accuracy: 0.8750
Epoch 182/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2913 - accuracy: 0.8965 - val_loss: 0.3280 - val_accuracy: 0.8733
Epoch 183/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2913 - accuracy: 0.8955 - val_loss: 0.3309 - val_accuracy: 0.8683
Epoch 184/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2904 - accuracy: 0.8971 - val_loss: 0.3262 - val_accuracy: 0.8683
Epoch 185/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2902 - accuracy: 0.8964 - val_loss: 0.3360 - val_accuracy: 0.8733
Epoch 186/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2911 - accuracy: 0.8968 - val_loss: 0.3249 - val_accuracy: 0.8650
Epoch 187/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2909 - accuracy: 0.8958 - val_loss: 0.3305 - val_accuracy: 0.8700
Epoch 188/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2889 - accuracy: 0.8972 - val_loss: 0.3251 - val_accuracy: 0.8700
Epoch 189/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2876 - accuracy: 0.8982 - val_loss: 0.3305 - val_accuracy: 0.8700
Epoch 190/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2884 - accuracy: 0.8974 - val_loss: 0.3266 - val_accuracy: 0.8733
Epoch 191/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2872 - accuracy: 0.8975 - val_loss: 0.3246 - val_accuracy: 0.8750
Epoch 192/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2864 - accuracy: 0.8983 - val_loss: 0.3226 - val_accuracy: 0.8717
Epoch 193/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2872 - accuracy: 0.8984 - val_loss: 0.3236 - val_accuracy: 0.8700
Epoch 194/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2859 - accuracy: 0.8983 - val_loss: 0.3319 - val_accuracy: 0.8767
Epoch 195/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2861 - accuracy: 0.8985 - val_loss: 0.3235 - val_accuracy: 0.8733
Epoch 196/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2854 - accuracy: 0.8983 - val_loss: 0.3279 - val_accuracy: 0.8733
Epoch 197/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2839 - accuracy: 0.8990 - val_loss: 0.3250 - val_accuracy: 0.8783
Epoch 198/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2847 - accuracy: 0.8992 - val_loss: 0.3256 - val_accuracy: 0.8667
Epoch 199/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2846 - accuracy: 0.8982 - val_loss: 0.3281 - val_accuracy: 0.8767
Epoch 200/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2825 - accuracy: 0.8993 - val_loss: 0.3222 - val_accuracy: 0.8733

# loss 값을 plot 해보겠습니다.
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))

plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.title('Loss graph without dropout layer') 
plt.ylim(0,1)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()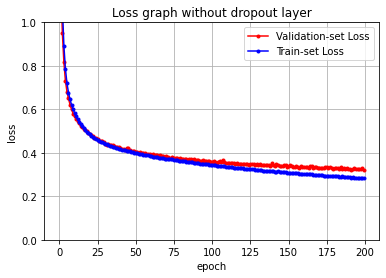

# accuracy 값을 plot 해보겠습니다.
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))

plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1) 
plt.title('Accuracy graph without dropout layer') 
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()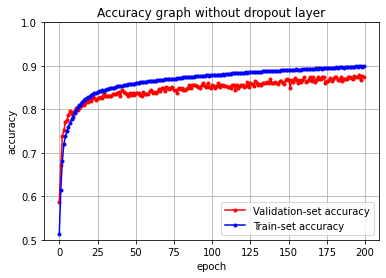

이렇게 오버피팅을 만든 환경에서 나머지 환경은 같게 실험해보자.

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(256, activation='relu'),
    # 여기에 dropout layer를 추가해보았습니다. 나머지 layer는 위의 실습과 같습니다. 
    keras.layers.Dropout(0.5),
    keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history= model.fit(X_train, y_train, epochs=200, batch_size=512, validation_data=(X_valid, y_valid))

Epoch 1/200
117/117 [==============================] - 1s 3ms/step - loss: 2.0632 - accuracy: 0.4626 - val_loss: 1.6692 - val_accuracy: 0.5517
Epoch 2/200
117/117 [==============================] - 0s 3ms/step - loss: 1.4476 - accuracy: 0.5548 - val_loss: 1.2078 - val_accuracy: 0.6617
Epoch 3/200
117/117 [==============================] - 0s 3ms/step - loss: 1.1437 - accuracy: 0.6274 - val_loss: 0.9981 - val_accuracy: 0.7083
Epoch 4/200
117/117 [==============================] - 0s 3ms/step - loss: 0.9806 - accuracy: 0.6718 - val_loss: 0.8681 - val_accuracy: 0.7417
Epoch 5/200
117/117 [==============================] - 0s 3ms/step - loss: 0.8791 - accuracy: 0.6999 - val_loss: 0.7862 - val_accuracy: 0.7517
Epoch 6/200
117/117 [==============================] - 0s 3ms/step - loss: 0.8115 - accuracy: 0.7176 - val_loss: 0.7295 - val_accuracy: 0.7750
Epoch 7/200
117/117 [==============================] - 0s 3ms/step - loss: 0.7652 - accuracy: 0.7285 - val_loss: 0.6905 - val_accuracy: 0.7850
Epoch 8/200
117/117 [==============================] - 0s 3ms/step - loss: 0.7319 - accuracy: 0.7373 - val_loss: 0.6640 - val_accuracy: 0.7850
Epoch 9/200
117/117 [==============================] - 0s 3ms/step - loss: 0.7065 - accuracy: 0.7466 - val_loss: 0.6424 - val_accuracy: 0.7933
Epoch 10/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6825 - accuracy: 0.7527 - val_loss: 0.6241 - val_accuracy: 0.7867
Epoch 11/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6656 - accuracy: 0.7604 - val_loss: 0.6097 - val_accuracy: 0.7900
Epoch 12/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6494 - accuracy: 0.7664 - val_loss: 0.5936 - val_accuracy: 0.7983
Epoch 13/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6330 - accuracy: 0.7731 - val_loss: 0.5824 - val_accuracy: 0.7917
Epoch 14/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6201 - accuracy: 0.7776 - val_loss: 0.5708 - val_accuracy: 0.7967
Epoch 15/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6081 - accuracy: 0.7818 - val_loss: 0.5612 - val_accuracy: 0.8000
Epoch 16/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5952 - accuracy: 0.7866 - val_loss: 0.5508 - val_accuracy: 0.7967
Epoch 17/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5876 - accuracy: 0.7911 - val_loss: 0.5430 - val_accuracy: 0.8000
Epoch 18/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5760 - accuracy: 0.7940 - val_loss: 0.5322 - val_accuracy: 0.8033
Epoch 19/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5673 - accuracy: 0.7981 - val_loss: 0.5288 - val_accuracy: 0.8033
Epoch 20/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5575 - accuracy: 0.8013 - val_loss: 0.5163 - val_accuracy: 0.8050
Epoch 21/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5494 - accuracy: 0.8057 - val_loss: 0.5100 - val_accuracy: 0.8167
Epoch 22/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5441 - accuracy: 0.8088 - val_loss: 0.5078 - val_accuracy: 0.8133
Epoch 23/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5369 - accuracy: 0.8099 - val_loss: 0.5010 - val_accuracy: 0.8200
Epoch 24/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5304 - accuracy: 0.8123 - val_loss: 0.4945 - val_accuracy: 0.8183
Epoch 25/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5238 - accuracy: 0.8149 - val_loss: 0.4897 - val_accuracy: 0.8200
Epoch 26/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5197 - accuracy: 0.8169 - val_loss: 0.4877 - val_accuracy: 0.8200
Epoch 27/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5143 - accuracy: 0.8185 - val_loss: 0.4799 - val_accuracy: 0.8200
Epoch 28/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5087 - accuracy: 0.8201 - val_loss: 0.4735 - val_accuracy: 0.8200
Epoch 29/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5033 - accuracy: 0.8214 - val_loss: 0.4731 - val_accuracy: 0.8183
Epoch 30/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5011 - accuracy: 0.8235 - val_loss: 0.4685 - val_accuracy: 0.8233
Epoch 31/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4947 - accuracy: 0.8253 - val_loss: 0.4623 - val_accuracy: 0.8183
Epoch 32/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4925 - accuracy: 0.8263 - val_loss: 0.4594 - val_accuracy: 0.8250
Epoch 33/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4889 - accuracy: 0.8283 - val_loss: 0.4599 - val_accuracy: 0.8167
Epoch 34/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4847 - accuracy: 0.8290 - val_loss: 0.4555 - val_accuracy: 0.8167
Epoch 35/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4813 - accuracy: 0.8299 - val_loss: 0.4498 - val_accuracy: 0.8200
Epoch 36/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4760 - accuracy: 0.8313 - val_loss: 0.4469 - val_accuracy: 0.8250
Epoch 37/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4738 - accuracy: 0.8326 - val_loss: 0.4464 - val_accuracy: 0.8317
Epoch 38/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4716 - accuracy: 0.8330 - val_loss: 0.4418 - val_accuracy: 0.8267
Epoch 39/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4683 - accuracy: 0.8361 - val_loss: 0.4424 - val_accuracy: 0.8283
Epoch 40/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4643 - accuracy: 0.8374 - val_loss: 0.4372 - val_accuracy: 0.8300
Epoch 41/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4628 - accuracy: 0.8359 - val_loss: 0.4363 - val_accuracy: 0.8267
Epoch 42/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4607 - accuracy: 0.8366 - val_loss: 0.4340 - val_accuracy: 0.8300
Epoch 43/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4561 - accuracy: 0.8390 - val_loss: 0.4310 - val_accuracy: 0.8350
Epoch 44/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4533 - accuracy: 0.8397 - val_loss: 0.4298 - val_accuracy: 0.8300
Epoch 45/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4496 - accuracy: 0.8413 - val_loss: 0.4271 - val_accuracy: 0.8317
Epoch 46/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4491 - accuracy: 0.8416 - val_loss: 0.4239 - val_accuracy: 0.8283
Epoch 47/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4461 - accuracy: 0.8429 - val_loss: 0.4242 - val_accuracy: 0.8283
Epoch 48/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4470 - accuracy: 0.8426 - val_loss: 0.4197 - val_accuracy: 0.8300
Epoch 49/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4433 - accuracy: 0.8429 - val_loss: 0.4187 - val_accuracy: 0.8367
Epoch 50/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4403 - accuracy: 0.8446 - val_loss: 0.4160 - val_accuracy: 0.8300
Epoch 51/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4366 - accuracy: 0.8450 - val_loss: 0.4131 - val_accuracy: 0.8350
Epoch 52/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4369 - accuracy: 0.8466 - val_loss: 0.4122 - val_accuracy: 0.8350
Epoch 53/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4331 - accuracy: 0.8470 - val_loss: 0.4108 - val_accuracy: 0.8350
Epoch 54/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4330 - accuracy: 0.8478 - val_loss: 0.4097 - val_accuracy: 0.8317
Epoch 55/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4311 - accuracy: 0.8477 - val_loss: 0.4075 - val_accuracy: 0.8333
Epoch 56/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4291 - accuracy: 0.8502 - val_loss: 0.4065 - val_accuracy: 0.8367
Epoch 57/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4253 - accuracy: 0.8496 - val_loss: 0.4046 - val_accuracy: 0.8300
Epoch 58/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4249 - accuracy: 0.8494 - val_loss: 0.4023 - val_accuracy: 0.8350
Epoch 59/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4241 - accuracy: 0.8500 - val_loss: 0.4024 - val_accuracy: 0.8350
Epoch 60/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4207 - accuracy: 0.8520 - val_loss: 0.4014 - val_accuracy: 0.8350
Epoch 61/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4186 - accuracy: 0.8526 - val_loss: 0.4002 - val_accuracy: 0.8383
Epoch 62/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4168 - accuracy: 0.8524 - val_loss: 0.3979 - val_accuracy: 0.8383
Epoch 63/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4152 - accuracy: 0.8527 - val_loss: 0.3963 - val_accuracy: 0.8300
Epoch 64/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4158 - accuracy: 0.8528 - val_loss: 0.3951 - val_accuracy: 0.8433
Epoch 65/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4142 - accuracy: 0.8521 - val_loss: 0.3938 - val_accuracy: 0.8367
Epoch 66/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4129 - accuracy: 0.8543 - val_loss: 0.3923 - val_accuracy: 0.8333
Epoch 67/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4111 - accuracy: 0.8559 - val_loss: 0.3896 - val_accuracy: 0.8367
Epoch 68/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4090 - accuracy: 0.8549 - val_loss: 0.3889 - val_accuracy: 0.8400
Epoch 69/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4090 - accuracy: 0.8552 - val_loss: 0.3857 - val_accuracy: 0.8433
Epoch 70/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4061 - accuracy: 0.8561 - val_loss: 0.3876 - val_accuracy: 0.8400
Epoch 71/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4046 - accuracy: 0.8583 - val_loss: 0.3855 - val_accuracy: 0.8417
Epoch 72/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4045 - accuracy: 0.8568 - val_loss: 0.3840 - val_accuracy: 0.8450
Epoch 73/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4024 - accuracy: 0.8580 - val_loss: 0.3825 - val_accuracy: 0.8433
Epoch 74/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4020 - accuracy: 0.8566 - val_loss: 0.3831 - val_accuracy: 0.8450
Epoch 75/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4018 - accuracy: 0.8594 - val_loss: 0.3805 - val_accuracy: 0.8433
Epoch 76/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3991 - accuracy: 0.8580 - val_loss: 0.3798 - val_accuracy: 0.8417
Epoch 77/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3975 - accuracy: 0.8594 - val_loss: 0.3798 - val_accuracy: 0.8450
Epoch 78/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3977 - accuracy: 0.8593 - val_loss: 0.3785 - val_accuracy: 0.8450
Epoch 79/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3957 - accuracy: 0.8594 - val_loss: 0.3734 - val_accuracy: 0.8467
Epoch 80/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3963 - accuracy: 0.8600 - val_loss: 0.3731 - val_accuracy: 0.8433
Epoch 81/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3933 - accuracy: 0.8606 - val_loss: 0.3749 - val_accuracy: 0.8433
Epoch 82/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3923 - accuracy: 0.8609 - val_loss: 0.3733 - val_accuracy: 0.8450
Epoch 83/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3902 - accuracy: 0.8626 - val_loss: 0.3718 - val_accuracy: 0.8433
Epoch 84/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3904 - accuracy: 0.8625 - val_loss: 0.3714 - val_accuracy: 0.8450
Epoch 85/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3884 - accuracy: 0.8626 - val_loss: 0.3745 - val_accuracy: 0.8467
Epoch 86/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3879 - accuracy: 0.8631 - val_loss: 0.3719 - val_accuracy: 0.8433
Epoch 87/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3868 - accuracy: 0.8633 - val_loss: 0.3661 - val_accuracy: 0.8450
Epoch 88/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3852 - accuracy: 0.8637 - val_loss: 0.3672 - val_accuracy: 0.8383
Epoch 89/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3851 - accuracy: 0.8650 - val_loss: 0.3660 - val_accuracy: 0.8433
Epoch 90/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3832 - accuracy: 0.8642 - val_loss: 0.3664 - val_accuracy: 0.8433
Epoch 91/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3835 - accuracy: 0.8637 - val_loss: 0.3635 - val_accuracy: 0.8433
Epoch 92/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3829 - accuracy: 0.8662 - val_loss: 0.3637 - val_accuracy: 0.8467
Epoch 93/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3816 - accuracy: 0.8653 - val_loss: 0.3629 - val_accuracy: 0.8517
Epoch 94/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3812 - accuracy: 0.8649 - val_loss: 0.3647 - val_accuracy: 0.8450
Epoch 95/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3777 - accuracy: 0.8662 - val_loss: 0.3624 - val_accuracy: 0.8450
Epoch 96/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3775 - accuracy: 0.8667 - val_loss: 0.3603 - val_accuracy: 0.8417
Epoch 97/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3767 - accuracy: 0.8662 - val_loss: 0.3603 - val_accuracy: 0.8450
Epoch 98/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3752 - accuracy: 0.8673 - val_loss: 0.3588 - val_accuracy: 0.8433
Epoch 99/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3778 - accuracy: 0.8672 - val_loss: 0.3593 - val_accuracy: 0.8433
Epoch 100/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3745 - accuracy: 0.8672 - val_loss: 0.3547 - val_accuracy: 0.8433
Epoch 101/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3736 - accuracy: 0.8676 - val_loss: 0.3572 - val_accuracy: 0.8467
Epoch 102/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3723 - accuracy: 0.8689 - val_loss: 0.3550 - val_accuracy: 0.8467
Epoch 103/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3701 - accuracy: 0.8686 - val_loss: 0.3581 - val_accuracy: 0.8450
Epoch 104/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3715 - accuracy: 0.8682 - val_loss: 0.3553 - val_accuracy: 0.8417
Epoch 105/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3691 - accuracy: 0.8695 - val_loss: 0.3549 - val_accuracy: 0.8450
Epoch 106/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3697 - accuracy: 0.8693 - val_loss: 0.3545 - val_accuracy: 0.8433
Epoch 107/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3694 - accuracy: 0.8703 - val_loss: 0.3540 - val_accuracy: 0.8450
Epoch 108/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3684 - accuracy: 0.8697 - val_loss: 0.3523 - val_accuracy: 0.8450
Epoch 109/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3678 - accuracy: 0.8711 - val_loss: 0.3515 - val_accuracy: 0.8500
Epoch 110/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3665 - accuracy: 0.8718 - val_loss: 0.3519 - val_accuracy: 0.8467
Epoch 111/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3657 - accuracy: 0.8719 - val_loss: 0.3483 - val_accuracy: 0.8517
Epoch 112/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3649 - accuracy: 0.8694 - val_loss: 0.3472 - val_accuracy: 0.8517
Epoch 113/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3650 - accuracy: 0.8702 - val_loss: 0.3493 - val_accuracy: 0.8550
Epoch 114/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3616 - accuracy: 0.8714 - val_loss: 0.3495 - val_accuracy: 0.8533
Epoch 115/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3617 - accuracy: 0.8716 - val_loss: 0.3463 - val_accuracy: 0.8533
Epoch 116/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3602 - accuracy: 0.8720 - val_loss: 0.3494 - val_accuracy: 0.8517
Epoch 117/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3618 - accuracy: 0.8726 - val_loss: 0.3483 - val_accuracy: 0.8517
Epoch 118/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3606 - accuracy: 0.8719 - val_loss: 0.3448 - val_accuracy: 0.8517
Epoch 119/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3617 - accuracy: 0.8731 - val_loss: 0.3459 - val_accuracy: 0.8517
Epoch 120/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3596 - accuracy: 0.8730 - val_loss: 0.3461 - val_accuracy: 0.8517
Epoch 121/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3566 - accuracy: 0.8734 - val_loss: 0.3427 - val_accuracy: 0.8600
Epoch 122/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3591 - accuracy: 0.8729 - val_loss: 0.3444 - val_accuracy: 0.8533
Epoch 123/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3561 - accuracy: 0.8738 - val_loss: 0.3420 - val_accuracy: 0.8533
Epoch 124/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3559 - accuracy: 0.8740 - val_loss: 0.3406 - val_accuracy: 0.8550
Epoch 125/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3576 - accuracy: 0.8720 - val_loss: 0.3435 - val_accuracy: 0.8550
Epoch 126/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3540 - accuracy: 0.8743 - val_loss: 0.3403 - val_accuracy: 0.8550
Epoch 127/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3548 - accuracy: 0.8754 - val_loss: 0.3396 - val_accuracy: 0.8533
Epoch 128/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3549 - accuracy: 0.8741 - val_loss: 0.3416 - val_accuracy: 0.8583
Epoch 129/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3553 - accuracy: 0.8748 - val_loss: 0.3393 - val_accuracy: 0.8583
Epoch 130/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3513 - accuracy: 0.8745 - val_loss: 0.3406 - val_accuracy: 0.8550
Epoch 131/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3533 - accuracy: 0.8756 - val_loss: 0.3392 - val_accuracy: 0.8533
Epoch 132/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3511 - accuracy: 0.8752 - val_loss: 0.3405 - val_accuracy: 0.8550
Epoch 133/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3518 - accuracy: 0.8745 - val_loss: 0.3381 - val_accuracy: 0.8567
Epoch 134/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3479 - accuracy: 0.8771 - val_loss: 0.3370 - val_accuracy: 0.8583
Epoch 135/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3481 - accuracy: 0.8764 - val_loss: 0.3346 - val_accuracy: 0.8500
Epoch 136/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3490 - accuracy: 0.8772 - val_loss: 0.3358 - val_accuracy: 0.8600
Epoch 137/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3478 - accuracy: 0.8770 - val_loss: 0.3371 - val_accuracy: 0.8600
Epoch 138/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3477 - accuracy: 0.8764 - val_loss: 0.3346 - val_accuracy: 0.8617
Epoch 139/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3466 - accuracy: 0.8760 - val_loss: 0.3326 - val_accuracy: 0.8600
Epoch 140/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3452 - accuracy: 0.8784 - val_loss: 0.3309 - val_accuracy: 0.8583
Epoch 141/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3459 - accuracy: 0.8767 - val_loss: 0.3351 - val_accuracy: 0.8633
Epoch 142/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3455 - accuracy: 0.8777 - val_loss: 0.3315 - val_accuracy: 0.8633
Epoch 143/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3431 - accuracy: 0.8773 - val_loss: 0.3310 - val_accuracy: 0.8650
Epoch 144/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3442 - accuracy: 0.8777 - val_loss: 0.3317 - val_accuracy: 0.8633
Epoch 145/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3419 - accuracy: 0.8775 - val_loss: 0.3321 - val_accuracy: 0.8617
Epoch 146/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3444 - accuracy: 0.8779 - val_loss: 0.3304 - val_accuracy: 0.8633
Epoch 147/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3441 - accuracy: 0.8789 - val_loss: 0.3329 - val_accuracy: 0.8633
Epoch 148/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3413 - accuracy: 0.8792 - val_loss: 0.3306 - val_accuracy: 0.8617
Epoch 149/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3428 - accuracy: 0.8784 - val_loss: 0.3298 - val_accuracy: 0.8617
Epoch 150/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3407 - accuracy: 0.8794 - val_loss: 0.3296 - val_accuracy: 0.8667
Epoch 151/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3393 - accuracy: 0.8801 - val_loss: 0.3284 - val_accuracy: 0.8583
Epoch 152/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3385 - accuracy: 0.8804 - val_loss: 0.3279 - val_accuracy: 0.8583
Epoch 153/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3388 - accuracy: 0.8794 - val_loss: 0.3300 - val_accuracy: 0.8617
Epoch 154/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3377 - accuracy: 0.8802 - val_loss: 0.3294 - val_accuracy: 0.8617
Epoch 155/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3369 - accuracy: 0.8809 - val_loss: 0.3293 - val_accuracy: 0.8700
Epoch 156/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3378 - accuracy: 0.8797 - val_loss: 0.3254 - val_accuracy: 0.8633
Epoch 157/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3363 - accuracy: 0.8809 - val_loss: 0.3278 - val_accuracy: 0.8667
Epoch 158/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3358 - accuracy: 0.8808 - val_loss: 0.3271 - val_accuracy: 0.8650
Epoch 159/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3350 - accuracy: 0.8812 - val_loss: 0.3259 - val_accuracy: 0.8700
Epoch 160/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3350 - accuracy: 0.8816 - val_loss: 0.3252 - val_accuracy: 0.8633
Epoch 161/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3349 - accuracy: 0.8828 - val_loss: 0.3236 - val_accuracy: 0.8650
Epoch 162/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3316 - accuracy: 0.8824 - val_loss: 0.3240 - val_accuracy: 0.8667
Epoch 163/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3316 - accuracy: 0.8823 - val_loss: 0.3236 - val_accuracy: 0.8650
Epoch 164/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3326 - accuracy: 0.8825 - val_loss: 0.3227 - val_accuracy: 0.8667
Epoch 165/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3337 - accuracy: 0.8812 - val_loss: 0.3237 - val_accuracy: 0.8667
Epoch 166/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3315 - accuracy: 0.8822 - val_loss: 0.3252 - val_accuracy: 0.8733
Epoch 167/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3302 - accuracy: 0.8830 - val_loss: 0.3222 - val_accuracy: 0.8633
Epoch 168/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3296 - accuracy: 0.8827 - val_loss: 0.3202 - val_accuracy: 0.8683
Epoch 169/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3287 - accuracy: 0.8842 - val_loss: 0.3194 - val_accuracy: 0.8683
Epoch 170/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3289 - accuracy: 0.8816 - val_loss: 0.3194 - val_accuracy: 0.8667
Epoch 171/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3276 - accuracy: 0.8850 - val_loss: 0.3232 - val_accuracy: 0.8700
Epoch 172/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3287 - accuracy: 0.8830 - val_loss: 0.3184 - val_accuracy: 0.8667
Epoch 173/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3291 - accuracy: 0.8840 - val_loss: 0.3217 - val_accuracy: 0.8683
Epoch 174/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3275 - accuracy: 0.8849 - val_loss: 0.3242 - val_accuracy: 0.8633
Epoch 175/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3251 - accuracy: 0.8842 - val_loss: 0.3223 - val_accuracy: 0.8667
Epoch 176/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3270 - accuracy: 0.8839 - val_loss: 0.3199 - val_accuracy: 0.8683
Epoch 177/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3262 - accuracy: 0.8838 - val_loss: 0.3196 - val_accuracy: 0.8683
Epoch 178/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3258 - accuracy: 0.8851 - val_loss: 0.3150 - val_accuracy: 0.8617
Epoch 179/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3234 - accuracy: 0.8855 - val_loss: 0.3195 - val_accuracy: 0.8683
Epoch 180/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3260 - accuracy: 0.8852 - val_loss: 0.3256 - val_accuracy: 0.8633
Epoch 181/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3245 - accuracy: 0.8844 - val_loss: 0.3213 - val_accuracy: 0.8683
Epoch 182/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3242 - accuracy: 0.8853 - val_loss: 0.3234 - val_accuracy: 0.8617
Epoch 183/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3227 - accuracy: 0.8857 - val_loss: 0.3200 - val_accuracy: 0.8650
Epoch 184/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3225 - accuracy: 0.8861 - val_loss: 0.3156 - val_accuracy: 0.8667
Epoch 185/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3233 - accuracy: 0.8857 - val_loss: 0.3175 - val_accuracy: 0.8633
Epoch 186/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3224 - accuracy: 0.8853 - val_loss: 0.3165 - val_accuracy: 0.8667
Epoch 187/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3209 - accuracy: 0.8868 - val_loss: 0.3216 - val_accuracy: 0.8583
Epoch 188/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3218 - accuracy: 0.8851 - val_loss: 0.3202 - val_accuracy: 0.8600
Epoch 189/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3195 - accuracy: 0.8862 - val_loss: 0.3155 - val_accuracy: 0.8583
Epoch 190/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3201 - accuracy: 0.8866 - val_loss: 0.3174 - val_accuracy: 0.8600
Epoch 191/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3236 - accuracy: 0.8846 - val_loss: 0.3133 - val_accuracy: 0.8650
Epoch 192/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3192 - accuracy: 0.8864 - val_loss: 0.3146 - val_accuracy: 0.8650
Epoch 193/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3195 - accuracy: 0.8872 - val_loss: 0.3176 - val_accuracy: 0.8683
Epoch 194/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3193 - accuracy: 0.8869 - val_loss: 0.3170 - val_accuracy: 0.8633
Epoch 195/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3180 - accuracy: 0.8866 - val_loss: 0.3125 - val_accuracy: 0.8667
Epoch 196/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3190 - accuracy: 0.8869 - val_loss: 0.3144 - val_accuracy: 0.8667
Epoch 197/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3174 - accuracy: 0.8867 - val_loss: 0.3132 - val_accuracy: 0.8650
Epoch 198/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3180 - accuracy: 0.8873 - val_loss: 0.3123 - val_accuracy: 0.8667
Epoch 199/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3158 - accuracy: 0.8877 - val_loss: 0.3098 - val_accuracy: 0.8650
Epoch 200/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3146 - accuracy: 0.8880 - val_loss: 0.3127 - val_accuracy: 0.8700

# loss 값을 plot 해보겠습니다. 
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))

plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.ylim(0,1)
plt.title('Loss graph with dropout layer') 
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()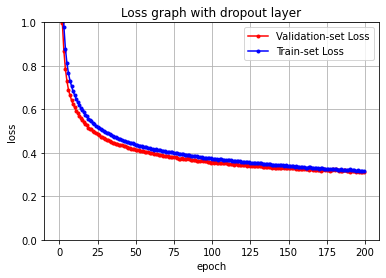

# accuracy 값을 plot 해보겠습니다. 
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))

plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1) 
plt.title('Accuracy graph with dropout layer') 
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()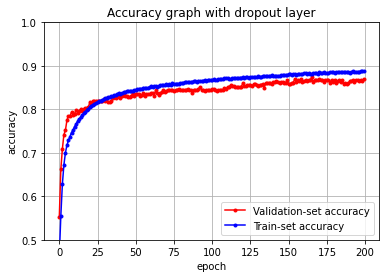

Batch Normalization

Batch Normalization은 gradient vanishing, explode 문제를 해결하는 방법이다.

논문 제목 : Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
논문 발표 시점 : 2015년
논문 링크 : 논문 PDF(https://arxiv.org/pdf/1502.03167.pdf)
참고 영상

(1) 실습

아무것도 하지 않은 fully connected layer와 Batch Normalization layer를 추가한 두 실험을 비교해보자. 정확도 비교와 속도의 차이에 초점을 맞추자

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt

fashion_mnist = keras.datasets.fashion_mnist
print('=3')

=3

# load mnist dataset (10 classes)
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
               'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

train_images = train_images / 255.0
test_images = test_images / 255.0

# split dataset and add dense layer

from sklearn.model_selection import train_test_split

X_train, X_valid, y_train, y_valid = train_test_split(train_images, train_labels, test_size=0.3, random_state=101)

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history= model.fit(X_train, y_train, epochs=20, batch_size=2048, validation_data=(X_valid, y_valid))

Epoch 1/20
21/21 [==============================] - 1s 17ms/step - loss: 1.2663 - accuracy: 0.5994 - val_loss: 0.7627 - val_accuracy: 0.7374
Epoch 2/20
21/21 [==============================] - 0s 7ms/step - loss: 0.6712 - accuracy: 0.7714 - val_loss: 0.6129 - val_accuracy: 0.7924
Epoch 3/20
21/21 [==============================] - 0s 6ms/step - loss: 0.5684 - accuracy: 0.8094 - val_loss: 0.5517 - val_accuracy: 0.8110
Epoch 4/20
21/21 [==============================] - 0s 6ms/step - loss: 0.5149 - accuracy: 0.8280 - val_loss: 0.5037 - val_accuracy: 0.8309
Epoch 5/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4820 - accuracy: 0.8384 - val_loss: 0.4830 - val_accuracy: 0.8364
Epoch 6/20
21/21 [==============================] - 0s 7ms/step - loss: 0.4569 - accuracy: 0.8461 - val_loss: 0.4648 - val_accuracy: 0.8397
Epoch 7/20
21/21 [==============================] - 0s 7ms/step - loss: 0.4399 - accuracy: 0.8494 - val_loss: 0.4495 - val_accuracy: 0.8465
Epoch 8/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4253 - accuracy: 0.8544 - val_loss: 0.4322 - val_accuracy: 0.8522
Epoch 9/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4110 - accuracy: 0.8601 - val_loss: 0.4233 - val_accuracy: 0.8552
Epoch 10/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4010 - accuracy: 0.8633 - val_loss: 0.4135 - val_accuracy: 0.8581
Epoch 11/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3919 - accuracy: 0.8653 - val_loss: 0.4104 - val_accuracy: 0.8592
Epoch 12/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3837 - accuracy: 0.8677 - val_loss: 0.4026 - val_accuracy: 0.8614
Epoch 13/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3748 - accuracy: 0.8709 - val_loss: 0.4015 - val_accuracy: 0.8589
Epoch 14/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3686 - accuracy: 0.8730 - val_loss: 0.3940 - val_accuracy: 0.8633
Epoch 15/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3629 - accuracy: 0.8750 - val_loss: 0.3870 - val_accuracy: 0.8654
Epoch 16/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3555 - accuracy: 0.8783 - val_loss: 0.3825 - val_accuracy: 0.8668
Epoch 17/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3501 - accuracy: 0.8795 - val_loss: 0.3831 - val_accuracy: 0.8658
Epoch 18/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3457 - accuracy: 0.8816 - val_loss: 0.3780 - val_accuracy: 0.8682
Epoch 19/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3422 - accuracy: 0.8809 - val_loss: 0.3751 - val_accuracy: 0.8687
Epoch 20/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3372 - accuracy: 0.8820 - val_loss: 0.3703 - val_accuracy: 0.8701

# loss 값을 plot 해보겠습니다. 
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))

plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.ylim(0,1)
plt.title('Loss graph without batch normalization') 
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

png

# accuracy 값을 plot 해보겠습니다. 
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))

plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1)
plt.title('Accuracy graph without batch normalization') 
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()

# batch

#
model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation='relu'),
    #여기에 batchnormalization layer를 추가해보았습니다. 나머지 layer는 위의 실습과 같습니다.
    keras.layers.BatchNormalization(),
    keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history= model.fit(X_train, y_train, epochs=20, batch_size=2048, validation_data=(X_valid, y_valid))

Epoch 1/20
21/21 [==============================] - 1s 18ms/step - loss: 0.9017 - accuracy: 0.6902 - val_loss: 1.0565 - val_accuracy: 0.6830
Epoch 2/20
21/21 [==============================] - 0s 6ms/step - loss: 0.5185 - accuracy: 0.8251 - val_loss: 0.8669 - val_accuracy: 0.7356
Epoch 3/20
21/21 [==============================] - 0s 7ms/step - loss: 0.4538 - accuracy: 0.8440 - val_loss: 0.7293 - val_accuracy: 0.7953
Epoch 4/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4143 - accuracy: 0.8579 - val_loss: 0.6455 - val_accuracy: 0.8363
Epoch 5/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3867 - accuracy: 0.8666 - val_loss: 0.6034 - val_accuracy: 0.8389
Epoch 6/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3676 - accuracy: 0.8719 - val_loss: 0.5492 - val_accuracy: 0.8532
Epoch 7/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3476 - accuracy: 0.8800 - val_loss: 0.5166 - val_accuracy: 0.8586
Epoch 8/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3338 - accuracy: 0.8840 - val_loss: 0.4928 - val_accuracy: 0.8639
Epoch 9/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3195 - accuracy: 0.8884 - val_loss: 0.4805 - val_accuracy: 0.8658
Epoch 10/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3083 - accuracy: 0.8912 - val_loss: 0.4541 - val_accuracy: 0.8636
Epoch 11/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2990 - accuracy: 0.8936 - val_loss: 0.4302 - val_accuracy: 0.8667
Epoch 12/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2886 - accuracy: 0.8977 - val_loss: 0.4265 - val_accuracy: 0.8660
Epoch 13/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2799 - accuracy: 0.9012 - val_loss: 0.4034 - val_accuracy: 0.8694
Epoch 14/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2702 - accuracy: 0.9036 - val_loss: 0.3812 - val_accuracy: 0.8762
Epoch 15/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2625 - accuracy: 0.9061 - val_loss: 0.3870 - val_accuracy: 0.8717
Epoch 16/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2561 - accuracy: 0.9085 - val_loss: 0.3681 - val_accuracy: 0.8752
Epoch 17/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2461 - accuracy: 0.9123 - val_loss: 0.3588 - val_accuracy: 0.8779
Epoch 18/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2380 - accuracy: 0.9160 - val_loss: 0.3789 - val_accuracy: 0.8643
Epoch 19/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2313 - accuracy: 0.9186 - val_loss: 0.3489 - val_accuracy: 0.8803
Epoch 20/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2268 - accuracy: 0.9203 - val_loss: 0.3600 - val_accuracy: 0.8734

# loss 값을 plot 해보겠습니다. 
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))

plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.ylim(0,1)
plt.title('Loss graph with batch normalization') 
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

# accuracy 값을 plot 해보겠습니다. 
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))

plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1) 
plt.title('Accurcy graph with batch normalization') 
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()

기존 fully connected layer도 낮지 않은 결과를 가져오지만, batch normalization을 추가하니 좀 더 빠른 정확도 향상이 있음을 확인할 수 있었다.

또한 loss function의 감소도 더 빨라짐을 확인할 수 있었다.

즉 Batch normalization으로 인해 이미지가 정규화되면서 좀 더 고른 분포를 가지기도 하며, ϵ 부분으로 인해 안정적인 학습이 가능해진다.

Jake

Nice to meet you. I would really appreciate your feedbacks. Thank you

이전 포스트