브레젠험 직선 알고리즘이란?
브레젠험 직선 알고리즘(Bresenham's line algorithm)은 컴퓨터 그래픽스에서 복잡하고 계산을 느리게 만드는 실수 계산을 배제하고 정수 계산만으로도 직선을 그리기 위해 만들어진 알고리즘이다.
직선의 공식을 이용해 계산된 좌표값은 컴퓨터 스크린에 표현하기 위해서는 소수점 이하를 버림 또는 반올림 등의 작업을 통해 정수로 만들게 된다.
이렇게 버려지는 소수점 이하의 복잡한 계산의 경우 속도 저하가 있을 수 있는데, 브레젠험 직선 알고리즘을 사용해 간단한 정수 연산으로 바꾸어 컴퓨터 스크린에 직선을 표현할 수 있다.
직선의 방정식
두 점을 지나는 직선의 방정식은 아래와 같다.
위 방정식은 일반적으로 와 같은 공식으로 표현된다. 여기에서 m은 직선의 기울기, n은 y절편의 값이라고도 한다.
컴퓨터 스크린에서의 직선
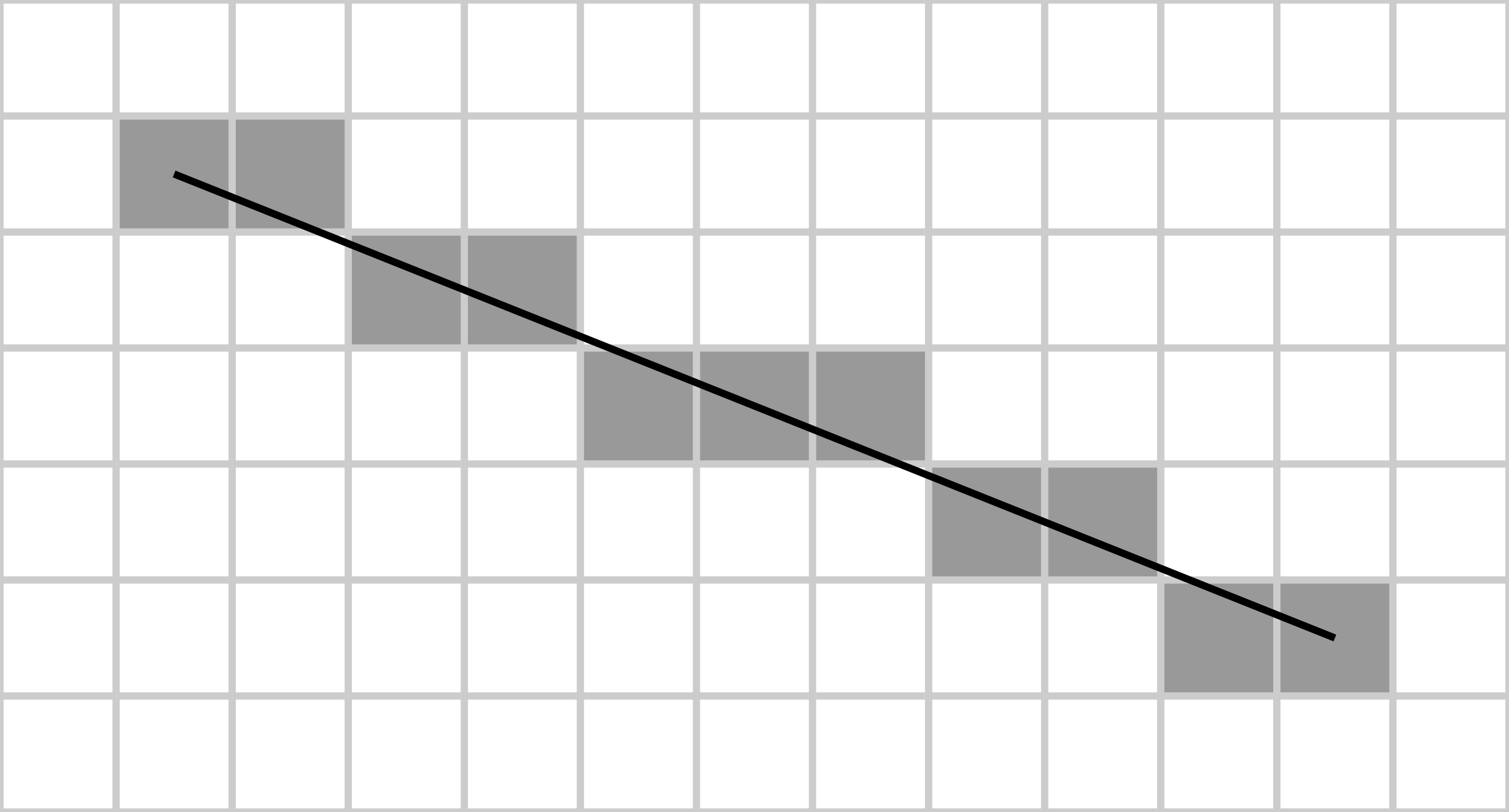 실제 컴퓨터 스크린은 픽셀(pixel) 단위로 이루어져 있다.
실제 컴퓨터 스크린은 픽셀(pixel) 단위로 이루어져 있다.
픽셀은 정수로 이루어져있어, 직선의 방정식을 통해 그려지는 직선이 여러 픽셀에 걸쳐져 있을 수 있다.
즉, 위 사진 처럼 직선이 여러 픽셀에 걸쳐져 있는 경우 어떤 픽셀을 표현하여 직선처럼 그려줄 것인지 판단하고 그려야 한다.
이러한 작업을 쉽고 빠르게 할 수 있도록 만들어 주는 것이 브레젠험 직선 알고리이다.
브레젠험 직선 알고리즘의 원리
브레젠험 직선 알고리즘은 처음에 x축과 y축 중 시작과 끝에서 변위가 큰 축을 선택하여, 변위가 큰 축을 기준으로 시작부터 끝까지 1씩 증가시키며 다른 축의 값의 가장 가까운 정수 값을 찾는 것이다.
변위
나중 위치의 값에서 처음 위치의 값을 뺀 벡터량 즉, 한 점의 최종 위치와 처음 위치 간의 차이
이러한 원리를 다음과 같은 과정을 통해 적용하며, 이는 기울기에 따라 다른 축을 기준으로 하기 때문에 약간의 차이점이 존재한다.
0 < 기울기 <= 1
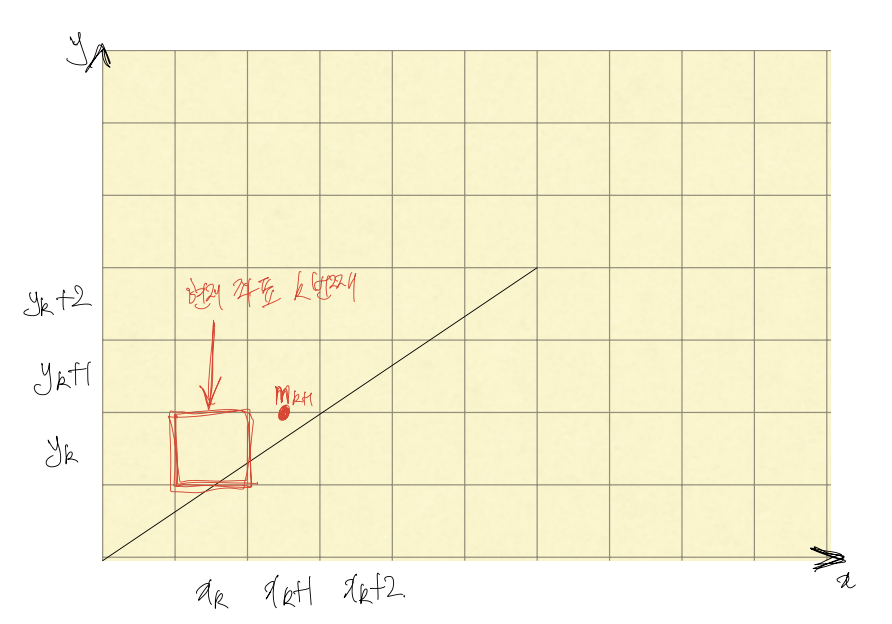 먼저 기울기가 0부터 1사이의 직선을 가정하고, 현재 좌표를 k번째라고 하고 해당 좌표를 라고 하자
먼저 기울기가 0부터 1사이의 직선을 가정하고, 현재 좌표를 k번째라고 하고 해당 좌표를 라고 하자
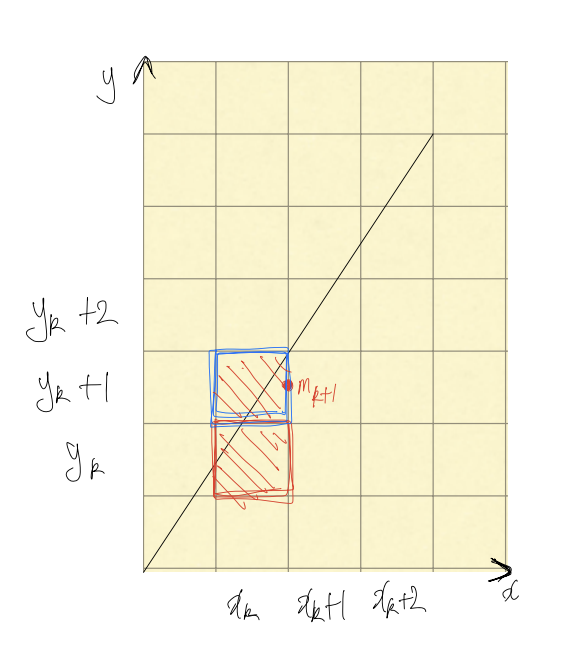
이제 현재 좌표에서 다음에 찍어야할 k+1번째 좌표값을 구하는데, x는 항상 1만큼 증가하고, y는 , 를 중단점()을 기준으로 선택한다.
- 중단점()이 임의로 설정한 직선 위에 존재할 경우 → y값은 선택
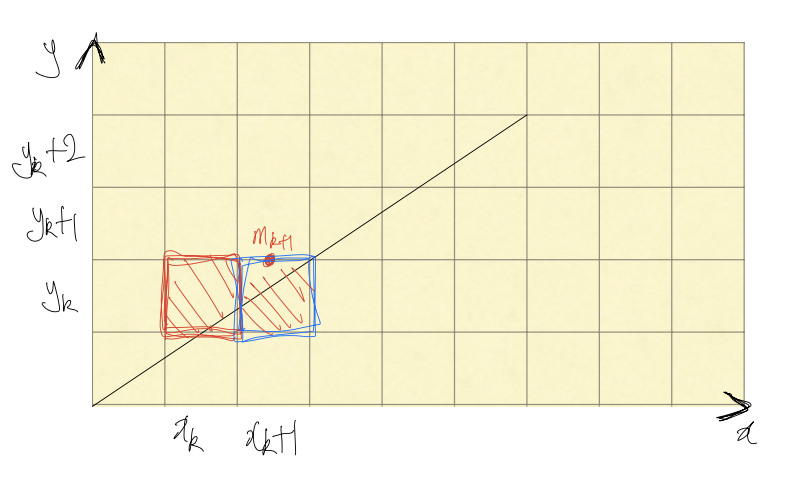
- 중단점()이 임의로 설정한 직선 아래에 존재할 경우 → y값은 1 증가한 선택
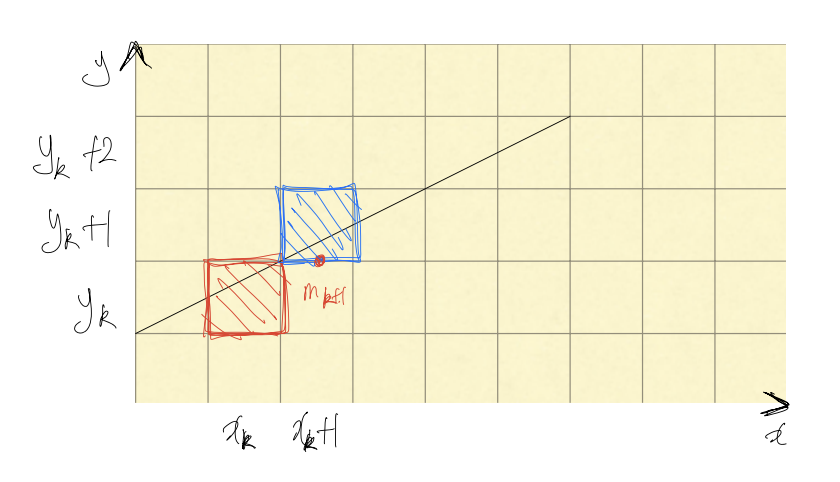
즉, 이를 위해 중단점()이 직선 위에 있는지 아래 있는지를 판단하는 판별식을 구해줘야 한다.
판별식을 구하는 방법은 다음과 같다.
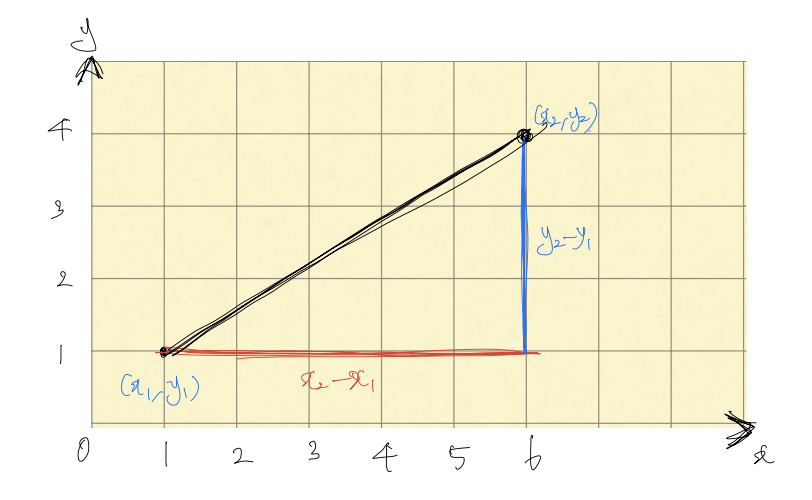
-
입력 받은 좌표 2개 , 로 직선의 방정식을 구한다.
-
이를 부등호 식로 나타낸다.
이라면
-
y값을 넘겨 한쪽을 0으로 나타낸다.
-
3번 식에 을 곱해 분모를 없애어 정수의 식으로 만들어준다.
-
4번 식에 정수 계산으로 만들어주기 위해 2를 곱하고, 정리해 판별식을 구한다.
이러한 일련의 과정을 통해 구한 판별식으로 중단점()을 판별한다.
그 후 그 다음 중단점인 을 결정하기 위한 판별식을 구한다.
- 인 경우(중단점이 직선 위에 있어 다음점 y값이 그대로였던 경우)
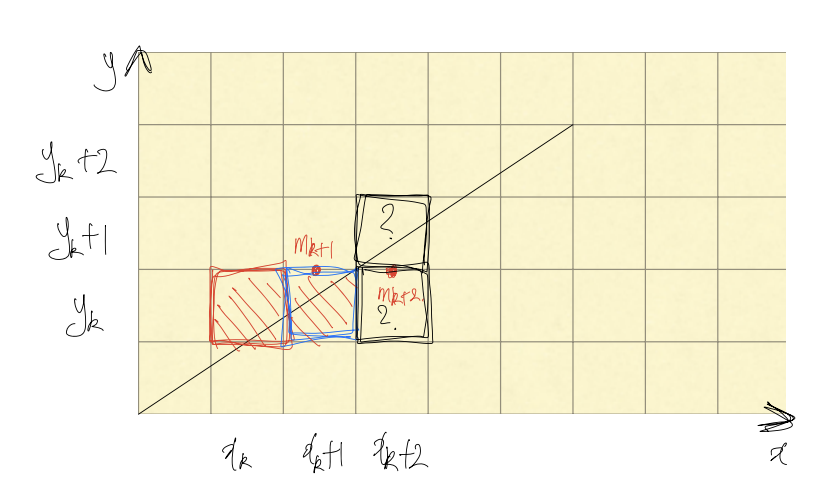 위 그림에서 의 좌표는 ()이다. 이를 판별식에 적용하면 다음과 같다.위 식를 과 비교해보면 만큼의 차이가 난다. 즉, 다음과 같은 관계식으로 나타낼 수 있다.
위 그림에서 의 좌표는 ()이다. 이를 판별식에 적용하면 다음과 같다.위 식를 과 비교해보면 만큼의 차이가 난다. 즉, 다음과 같은 관계식으로 나타낼 수 있다. - 인 경우(중단점이 직선 위에 있어 다음점 y값이 1 증가했을 경우)
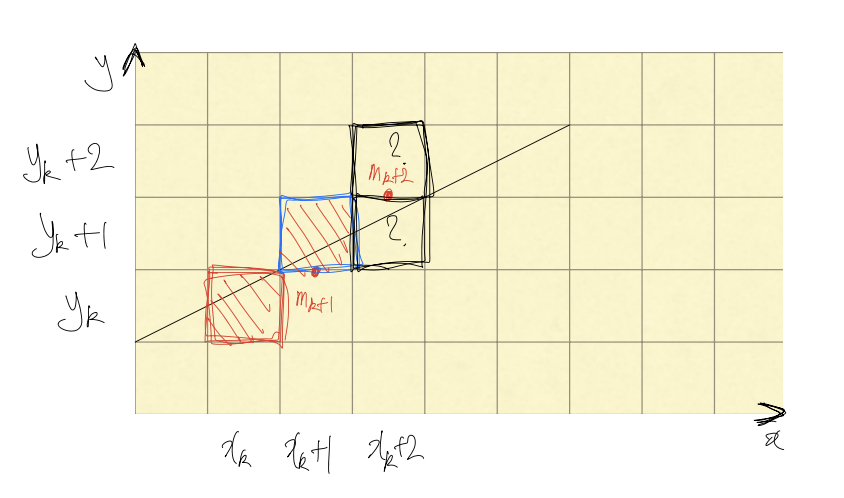 이 경우 의 좌표는 ()이다. 이를 판별식에 적용하면 다음과 같다.위 식를 과 비교해보면 다음과 같은 관계식을 얻을 수 있다.
이 경우 의 좌표는 ()이다. 이를 판별식에 적용하면 다음과 같다.위 식를 과 비교해보면 다음과 같은 관계식을 얻을 수 있다.
이러한 판별식의 관계를 이용하면 브레젠헴 알고리즘을 구현할 수 있는데, 판별식의 초기값 은 다음과 같이 구할 수 있다.
이제 다음 픽셀 위치의 결정 및 판별식 갱신식을 알게 되었으므로, 브레젠헴 알고리즘을 구현할 수 있다.
브레젠험 직선 알고리즘 구현 (0< 기울기 <= 1)
// bresenham algorithm by c
/*
s_x: x starting point
s_y: y starting point
f_x: x finishing point
f_y: y finishing point
*/
void bresenham(int s_x, int s_y, int f_x, int f_y)
{
// 0 < 기울기 <= 1
// 처음 찍을 점은 시작점으로 한다.
int x = s_x;
int y = s_y;
int W = f_x - s_x;
int H = f_y - s_y;
// 초기값
int F = 2 * H - W;
// 각 판별식 공식
int dF_1 = 2 * H;
int dF_2 = 2 * (H - W);
for (x; x <= f_x; x++)
{
// 점 그리기
draw_pixel(x, y);
// 중단점이 0보다 작으면 그에 맞는 판별식으로 갱신, y 값은 그대로
if (F < 0)
F += dF_1;
// 중단점이 0보다 크거나 같으면 그에 맞는 판별식으로 갱신, y 값 증가
else
{
y++;
F += dF_2;
}
}
}기울기 > 1
앞서 브레젠험 직선 알고리즘의 원리를 언급할 때, 브레젠험 직선 알고리즘은 처음에 x축과 y축 중 시작과 끝에서 변위가 큰 축을 기준으로 한다고 하였다.
위에서 기울기의 절대값이 1 이하일 경우 x축에서의 변위가 크기 때문에 x축을 기준으로 하였다.
하지만 기울기의 절대값이 1보다 큰경우 y축에서의 변위가 크기 때문에 y축을 기준으로하여 기울기의 절대값이 1 이하일 경우와 비슷한 방법으로 브레젠험 직선 알고리즘을 구현하면 된다.
 기울기의 절대값이 1보다 클 경우 위와 같은 상황이 될 것이고, 현재 좌표를 앞서 동일하게 k번째라고 하고 해당 좌표를 라고 하자.
기울기의 절대값이 1보다 클 경우 위와 같은 상황이 될 것이고, 현재 좌표를 앞서 동일하게 k번째라고 하고 해당 좌표를 라고 하자.
이제 현재 좌표에서 다음에 찍어야할 k+1번째 좌표값을 구하는데, 여기에서는 y는 항상 1만큼 증가하고, x는 , 를 중단점()을 기준으로 선택한다.
- 중단점()이 임의로 설정한 직선 위에 존재할 경우(y축 기준) → x값은 선택
- 중단점()이 임의로 설정한 직선 아래에 존재할 경우(y축 기준) → x값은 1 증가한 선택
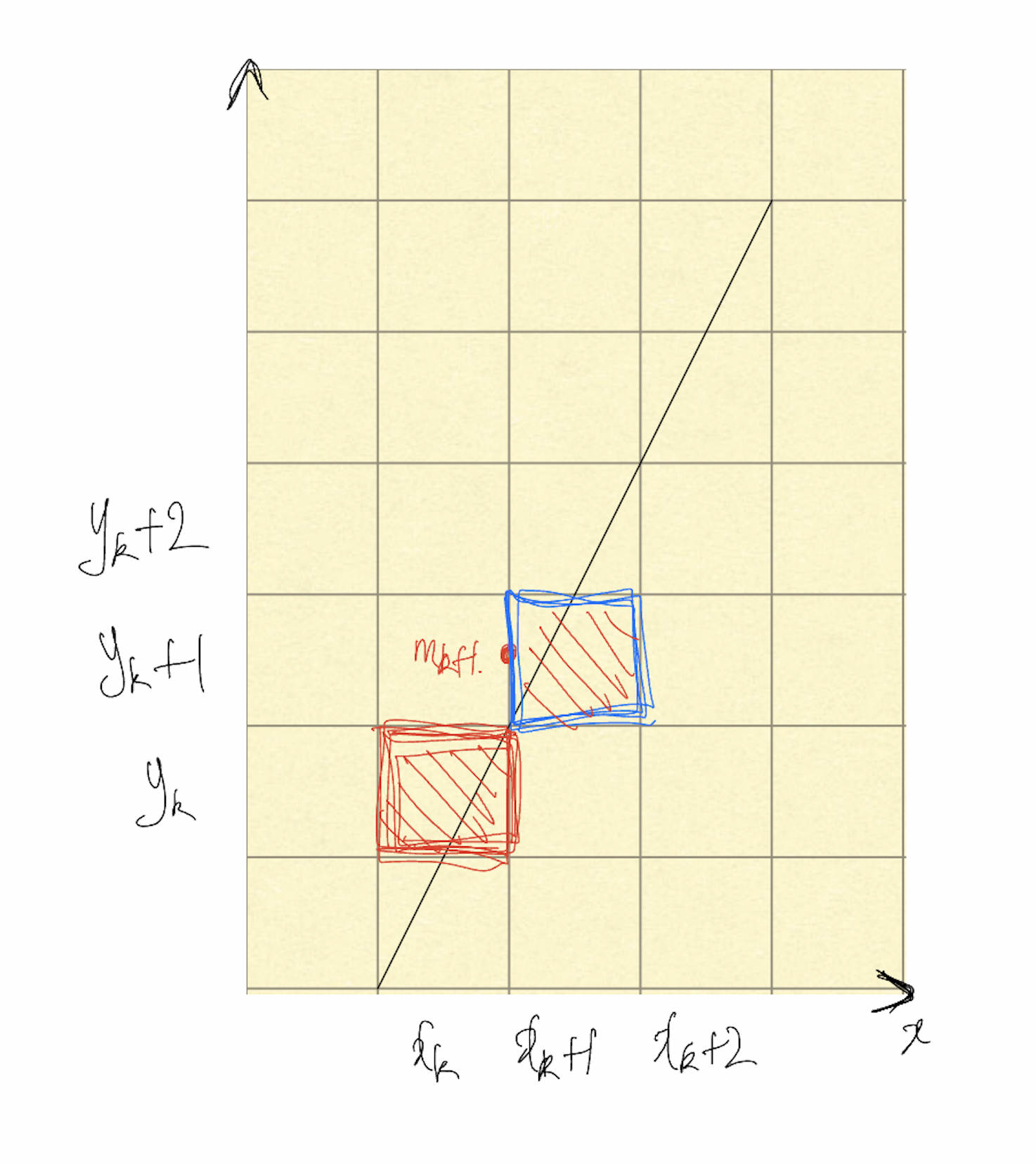
이를 위해 중단점()이 직선 위에 있는지 아래 있는지를 판단하는 판별식을 구해줘야 하는데, 이 원리는 위와 같은 방법(기준은 y축)으로 구해져 다음과 같이 얻을 수 있다.
- 해당 좌표가 직선보다 위
- 해당 좌표가 직선보다 아래
이제 판별식으로 중단점()을 판별한다.
그리고 위와 같은 방법으로 판별식 사이의 관계를 나타내면 다음과 같다.
- 인 경우(중단점이 직선 위에 있어 다음점 x값이 그대로였던 경우)
- 인 경우(중단점이 직선 위에 있어 다음점 x값이 1 증가했을 경우)
판별식의 초기값 은 다음과 같이 구할 수 있다.
이제 다음 픽셀 위치의 결정 및 판별식 갱신식을 알게 되었으므로, 브레젠헴 알고리즘을 구현할 수 있다.
브레젠험 직선 알고리즘 구현 (기울기 > 1)
// bresenham algorithm by c
/*
s_x: x starting point
s_y: y starting point
f_x: x finishing point
f_y: y finishing point
*/
void bresenham(int s_x, int s_y, int f_x, int f_y)
{
// 기울기 > 1
// 처음 찍을 점은 시작점으로 한다.
int x = s_x;
int y = s_y;
int W = f_x - s_x;
int H = f_y - s_y;
// 초기값
int F = 2 * W - H;
// 각 판별식 공식
int dF_1 = 2 * W;
int dF_2 = 2 * (W - H);
for (y; y <= f_y; y++)
{
// 점 그리기
draw_pixel(x, y);
// 중단점이 0보다 작으면 그에 맞는 판별식으로 갱신, x 값은 그대로
if (F < 0)
F += dF_1;
// 중단점이 0보다 크거나 같으면 그에 맞는 판별식으로 갱신, x 값 증가
else
{
x++;
F += dF_2;
}
}
}참고자료
https://en.wikipedia.org/wiki/Bresenham's_line_algorithm
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=ndb796&logNo=221115220322
https://playground10.tistory.com/62
https://kukuta.tistory.com/186
https://sulinep.blogspot.com/2020/05/bresenhams-line-algorithm.html