[FdF] 등각 투영법 (Isometric Projection)

등각 투영법이란??

등각 투영법(Isometric Drawing)은 기술 및 엔지니어링 도면에서 3차원 개체를 2차원으로 시각적으로 표현하는 방법이다.
3개의 좌표 축이 동일하게 축소되어 표시되고 그 중 2개 사이의 각도가 120인 축척 투영법이다.

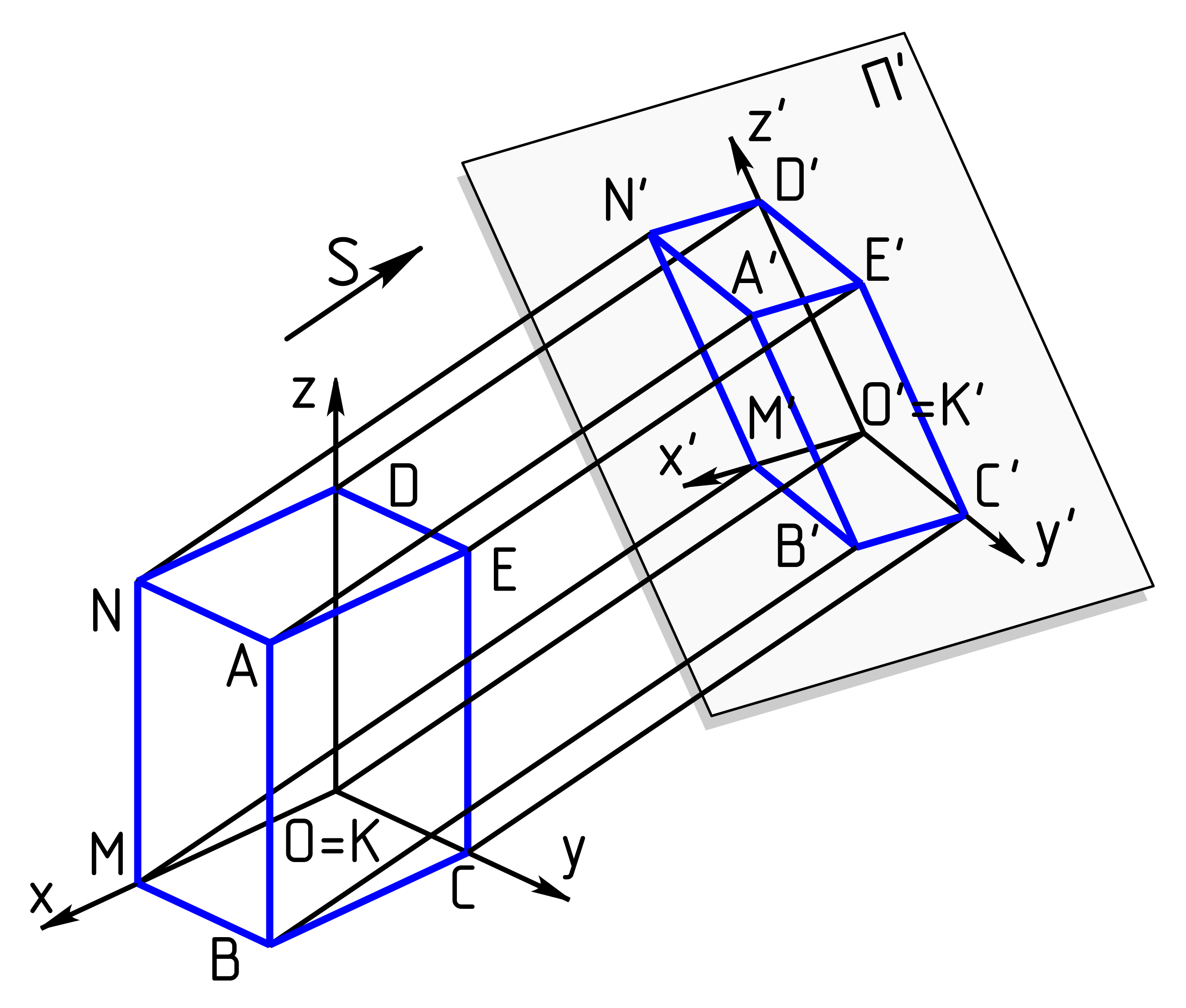
등각 투영 계산

관찰자가 보는 팔분면에 따라 등각 투영을 얻기 위한 8가지 다른 방향이 있다.
3D 공간에서의 점 $a_{x, y, z}$ 에서 2D 공간에서의 점 $b_{x, y}$ 로의 등각 변환은 회전 행렬을 사용해 다음과 같이 수학적으로 작성할 수 있다.

$\begin{bmatrix}c_x\\c_y\\c_z \end{bmatrix}$ $=$ $\begin{bmatrix}1&0&0\\0&cos(a)&sin(a)\\0&-sin(a)&cos(a) \end{bmatrix}$$\begin{bmatrix}cos(ß)&0&-sin(ß)\\0&1&0\\sin(ß)&0&cos(ß) \end{bmatrix}$$\begin{bmatrix}a_x\\a_y\\a_z \end{bmatrix}$

　　　 $=$ $1\over\sqrt6$$\begin{bmatrix}\sqrt3&0&-\sqrt3\\1&2&1\\\sqrt2&-\sqrt2&\sqrt2 \end{bmatrix}$$\begin{bmatrix}a_x\\a_y\\a_z \end{bmatrix}$

$(a = arcsin(tan(30\degree)) \simeq 35.264\degree,\; ß = 45\degree)$

위에 수식은 수직(여기에서 y) 축을 중심으로 $ß$ 만큼 회전한 다음 수평(여기에서는 x) 축을 중심으로 $a$만큼 회전하는 것이다. 그런 다음 xy 평면에 대한 직교 투영이 이어진다.

$\begin{bmatrix}b_x\\b_y\\0 \end{bmatrix}$ $=$ $\begin{bmatrix}1&0&0\\0&1&0\\0&0&0 \end{bmatrix}$$\begin{bmatrix}c_x\\c_y\\c_z \end{bmatrix}$

다른 7가지 방향은 회전하거나, 회전하지 않은 경우 또는 관찰 방향을 반전하는 등으로 얻어낼 수 있다.

Some 3D shapes are using the isometric drawing method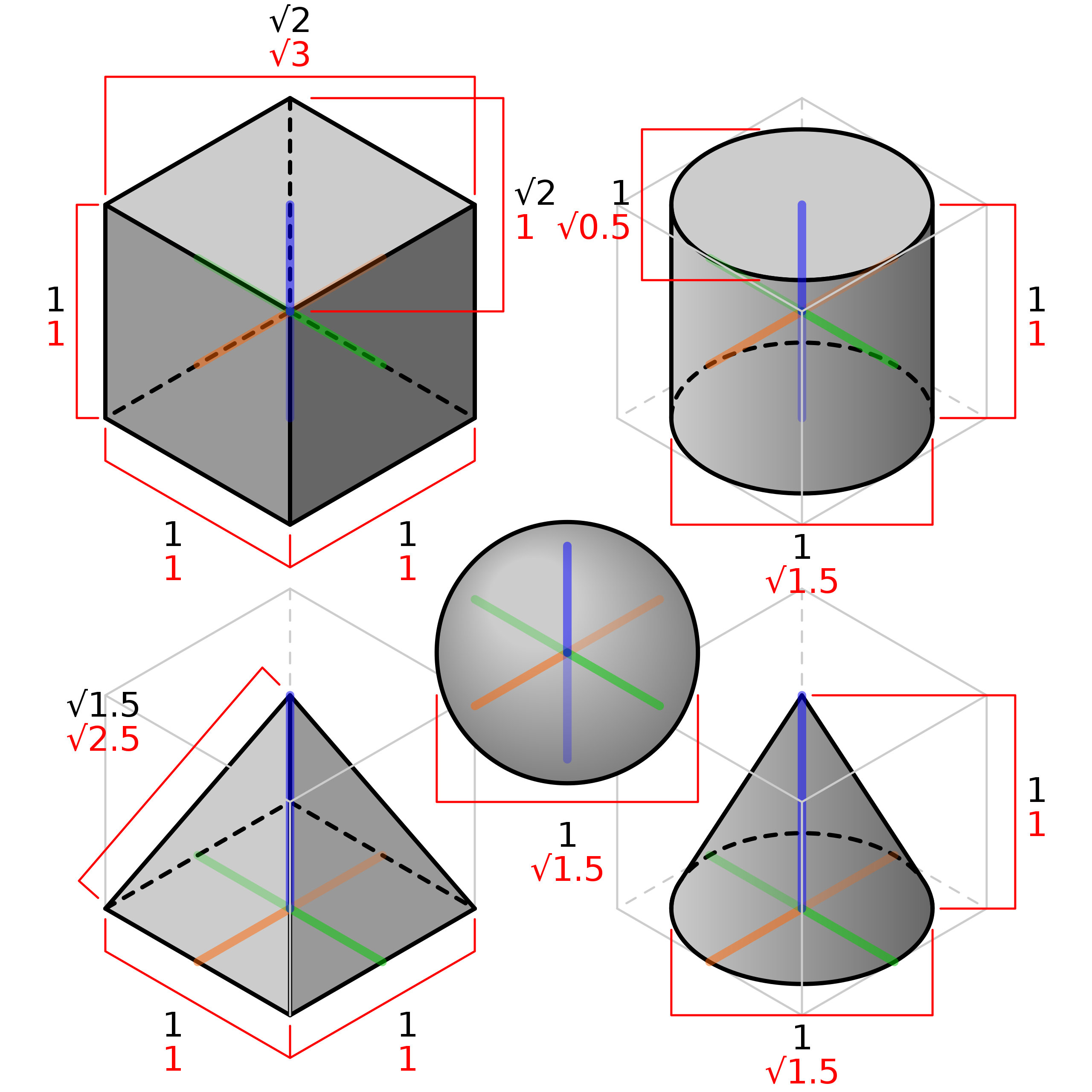

Camera rotations needed to achieve this perspective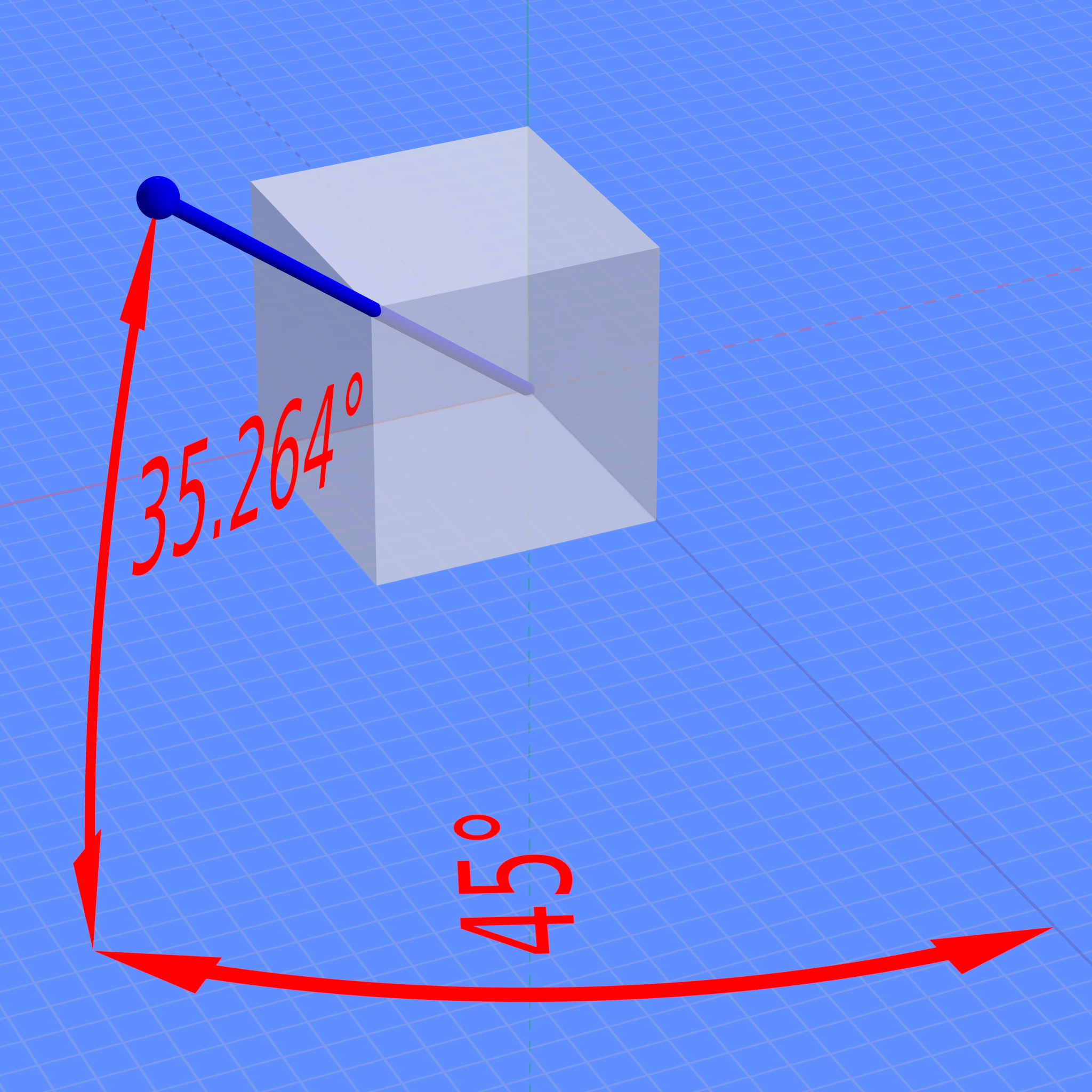

Isometric drawing of a cube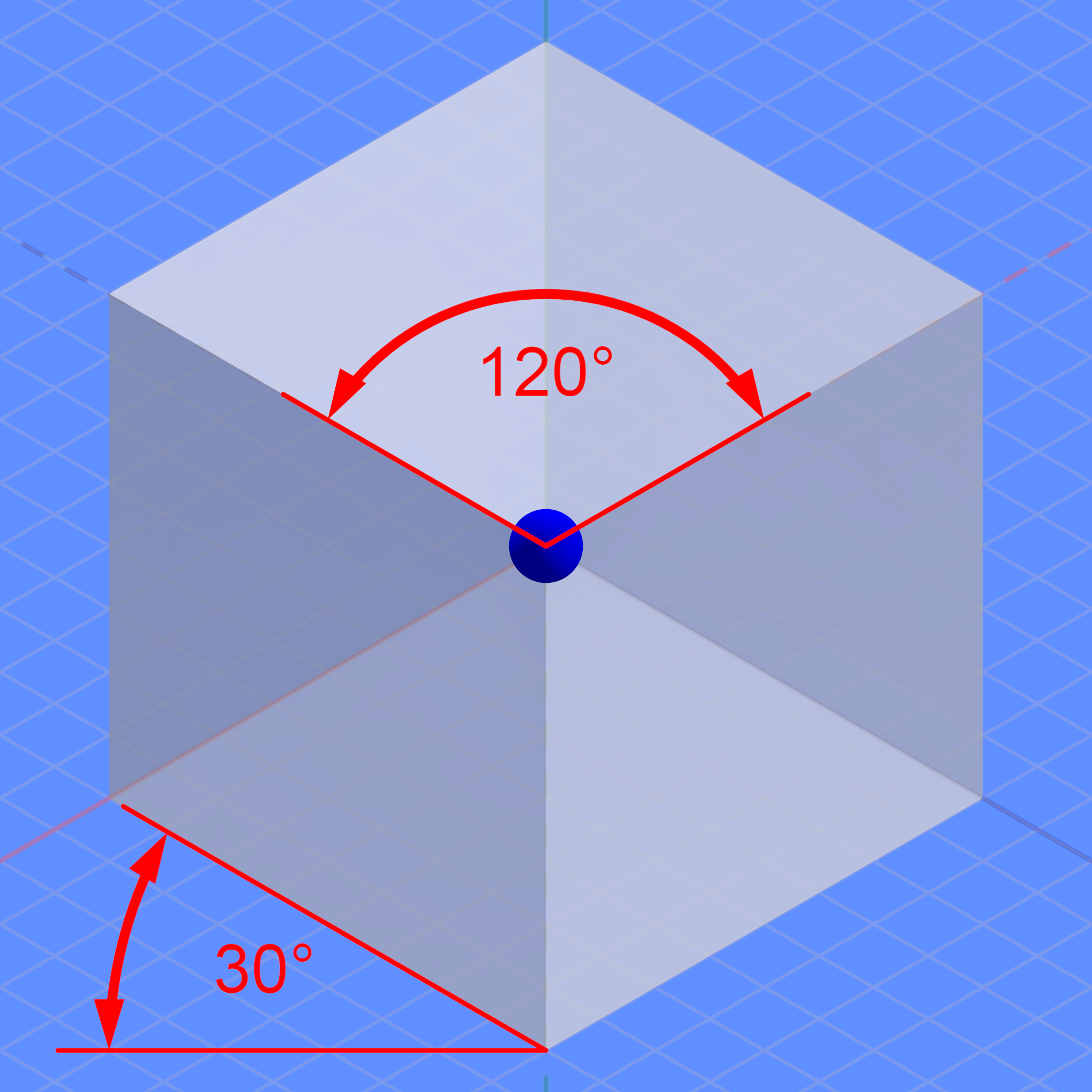

참고자료
https://en.wikipedia.org/wiki/Isometric_projection
https://m.blog.naver.com/kimjw1218/70178629876
https://en.wikipedia.org/wiki/Rotation_matrix
https://ko.wikipedia.org/wiki/%ED%9A%8C%EC%A0%84%EB%B3%80%ED%99%98%ED%96%89%EB%A0%AC