Algorithm Review 4

⭐Main Concept of Recursion
In terms of how recursion is similar to iteration, both techniques involve repeating a set of instructions multiple times to solve a problem. However, recursion involves calling the same function repeatedly, while iteration uses loops to repeat a set of instructions. In some cases, recursion can be simpler and more elegant than iteration, but it can also be less efficient and more prone to stack overflow errors if not implemented correctly.

1. Tower of Hanoi

• pseudo code

If n is 1 (the last disk is left):
	Move the disk from the starting peg to the destination peg.
Else:
	1. Move the top n-1 disks from the starting peg to the intermediate peg, using the destination peg as a buffer.
    
	2. Move the last disk from the starting peg to the destination peg.
    
	3. Move the n-1 disks from the intermediate peg to the destination peg, using the starting peg as a buffer.

• Code

void showMoves(int n, char start, char dest, char temp) {
	if (n == 1) {
		printf("Move disk 1 from peg %c to peg %c\n", start, dest);
	}
	else {
		showMoves(n - 1, start, temp, dest);
		printf("Move disk %d from peg %c to peg %c\n", n, start, dest);
		showMoves(n - 1, temp, dest, start);
	}
}

2. Maze

bool findMazePath2(int x, int y) {
	if (x == N - 1 && y == N - 1) {
		// The current position is the exit.
		maze[x][y] = PATH_COLOUR;
		return true;
	}
	else {
		if (x < 0 || y < 0 || x >= N || y >= N || maze[x][y] != PATHWAY_COLOUR) {
			// The path is not available.
			return false;
		}

		// Mark the current position as visited.
		maze[x][y] = PATHWAY_COLOUR;

		if (findMazePath2(x - 1, y) || findMazePath2(x, y + 1) || findMazePath2(x + 1, y) || findMazePath2(x, y - 1)) {
			// If any direction from the current position leads to the exit, return true.
			return true;
		}

		// No possible paths from this way
		maze[x][y] = BLOCKED_COLOUR;

		return false;
	}
}

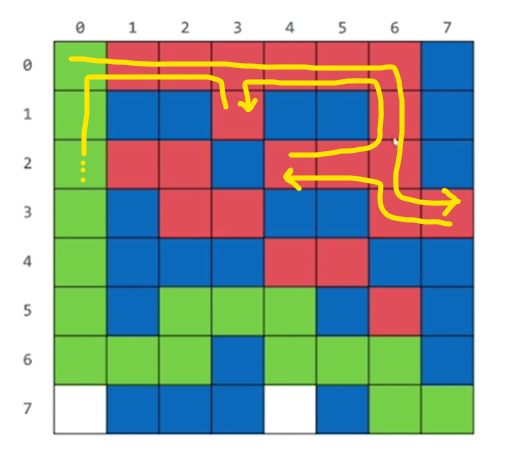
The endpoint of each yellow arrow represents the point where the program reaches the sentence that changes the position to BLOCKED_COLOUR and returns false.

3. Counting Blobs

int countBlob(int x, int y) {
	if (!isValid(x,y) || cells[x][y] != IMAGE_PIXEL)
		// Not part of the blob
		return 0;
	else {
		// count current pixel as part of the blob
		int numOfBlob = 1;
		// mark the pixel as visited
		cells[x][y] = VISITED_PIXEL;

		// Add the number of adjacent pixels that are part of the blob to the current count
 		for (int i = 0; i < 8; i++) {
			int x1 = x + offset[i][0];
			int y1 = y + offset[i][1];
			numOfBlob += countBlob(x1, y1);
		}
		// return the result
		return numOfBlob;
	}
}

N-Queens

In the case of the N-queens problem, we use the range 1 to N to represent the columns on the chessboard, which is why the loops start from 1 instead of 0.

bool promising(int level) {
	for (int i = 1; i < level; i++) {
		// Check if any two queens are in the same column
		if (cols[i] == cols[level])
			return false;
		// Check if any two queens are in the same diagonal
		if (abs(cols[i] - cols[level]) == level - i)
			return false;
	}
	return true;
}

bool queens(int level) {
	if (!promising(level)) {
		// non-promising
		return false;
	}

	else if (level == N) {
		// success
		for (int i = 1; i <= N; i++) {
			printf("%d, %d\n", i, cols[i]);
		}
		return true;
	}
	else {
		for (int i = 1; i <= N; i++) {
			// check possibilities for the next level
 			cols[level+1] = i;
			if (queens(level+1)) {
				return true;
			}
		}
		return false;
	}
}