Algorithm Review 6

Printing Power Set

1. 기본 알고리즘

1) {a, b, c, d, e}의 멱집합은 총 2^n가지이다.

• 이는 {b, c, d, e}의 모든 부분집합 2^(n-1)가지와 {b, c, d, e}로 이루어진 모든 부분집합에 {a}를 합한 2^(n-1)가지로 나눌 수 있다.
• {b, c, d, e}|의 멱집합을 구하는 방법은 다시 {c, d, e}로 이루어진 모든 부분집합과 그 집합들에 {b}를 더한 집합들로 나눌 수 있다.

2) Recursive Case에서 재귀함수는 입력받은 원소를 이용하여 만들 수 있는 모든 부분집합들을 리턴해야 한다.

• PowerSet(P, S)를 함수의 signature로 사용할 수 있다.
• S는 부분집합을 만들 원소의 집합을 의미한다.
• P는 만들어진 부분집합에 더해줄 원소를 의미한다.
• 위의 예에서 PowerSet(∅, {a, b, c, d, e}) = PowerSet(∅, {b, c, d, e}) ∪ PowerSet({a}, {b, c, d, e})가 된다.

3) boolean 배열을 사용하면 매개변수 P와 S를 쉽게 표현할 수 있다.

• include 배열의 index를 나타내는 k로 집합 P와 S를 나눌 수 있다.
• P는 처음부터 k-1까지의 원소 중 일부이고, S는 k부터 마지막까지 연속된 원소들이다.
• 각 index (k)는 해당 원소를 부분집합에 더해줘야 하면 (P에 속하면) true, 아니면 false이다.

4) S가 ∅일 때, 해당 경우의 P를 출력한다.

• k가 n가 되면 집합 P (모든 원소에 다한 include의 true false)가 결정된다. 이는 S가 ∅이 되는 것과 같다.
• include배열의 값에 따른 원소 집합인 P를 출력한다.

2. 다이어그램

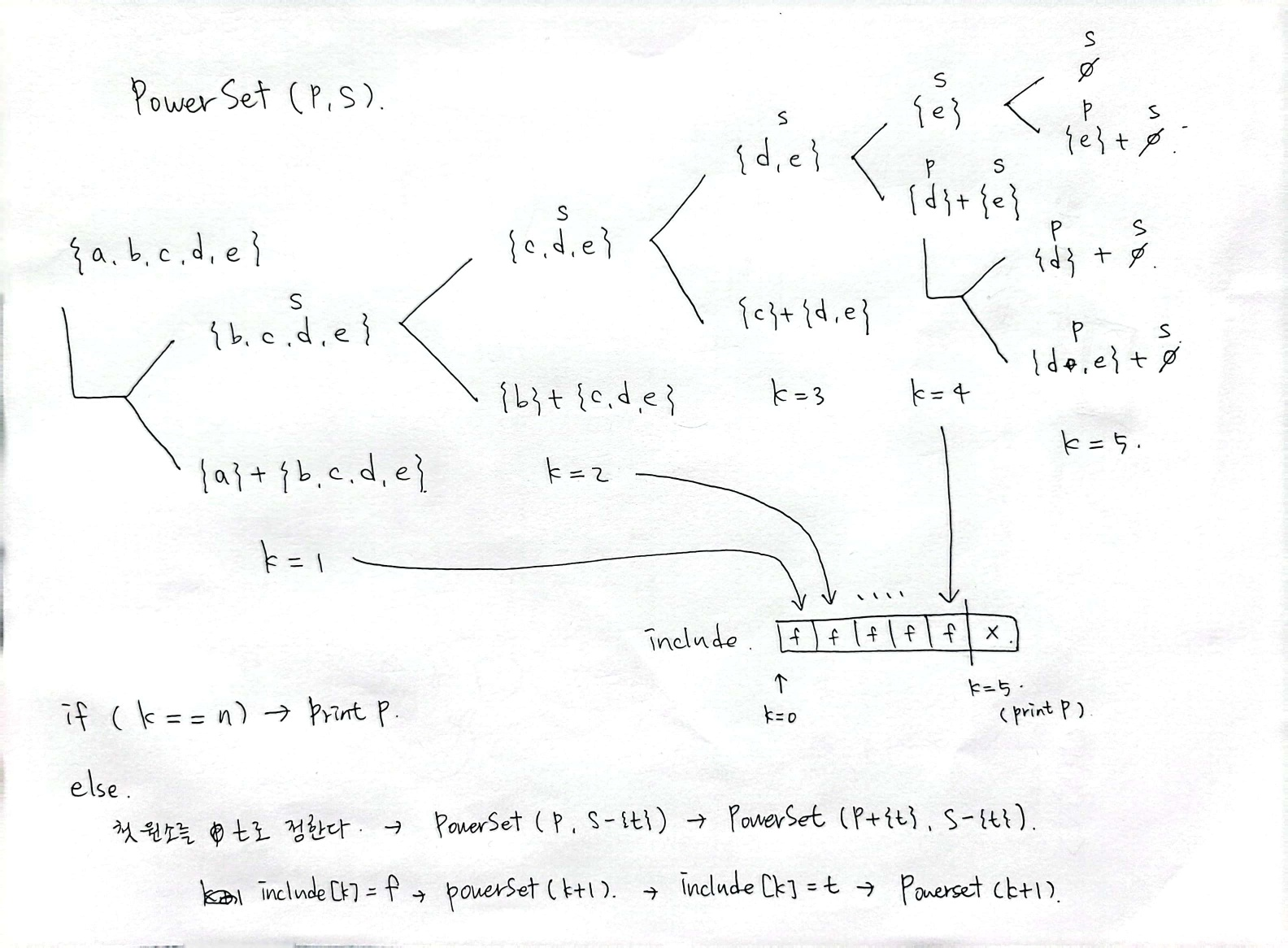
3. 코드

#include <stdio.h>
#include <stdbool.h>

char data[] = { 'a', 'b', 'c', 'd', 'e'};
int n = 5;
bool include[5];
void powerSet(int k) {
	if (k == n) {
    	// print P
		for (int i = 0; i < n; i++) {
			if (include[i]) printf("%c ", data[i]);
		}
		printf("\n");
		return;
	}
	
    // To get power sets for {a, b, c, d, e}
    // Set {a] as false in P
	include[k] = false;
  	// Get power sets for S, {b, c, d, e}
	powerSet(k + 1);
    // Set {a} as true in P
	include[k] = true;
    // Get power sets for S, {b, c, d, e}
	powerSet(k + 1);
}

int main() {
	powerSet(0);
}

4. 상태공간트리

알고리즘을 다음과 같이 표현할 수 있다.

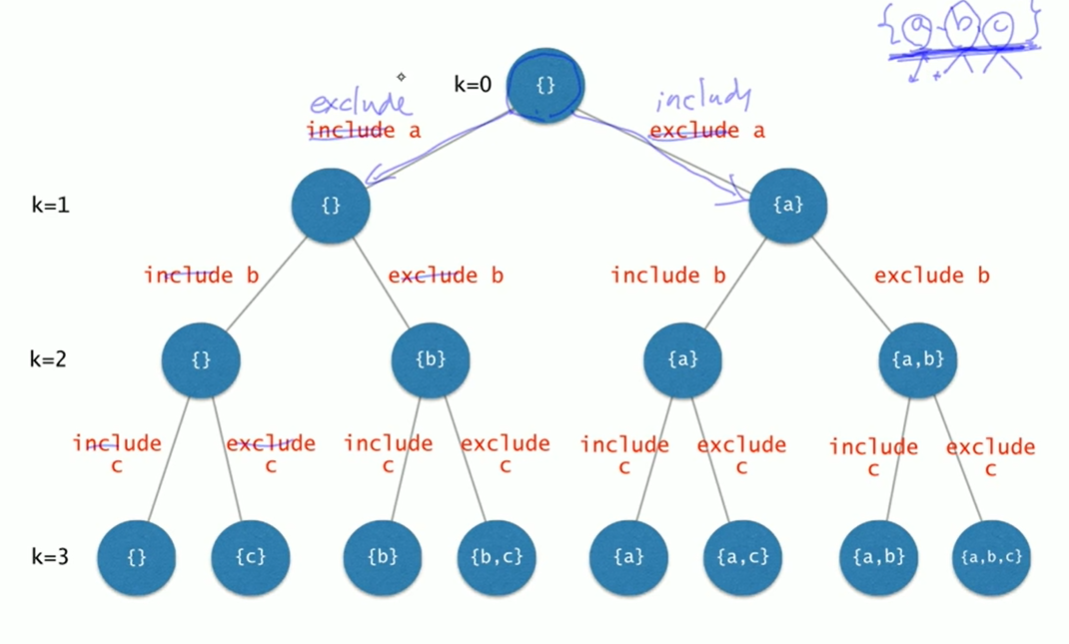
• include 배열과 k는 트리상에서 현재 나의 위치를 나타낸다.
• include = {false, true, false}이고, k = 2인 경우는 그림 상에서 상태가 {b}인 부모 노드이다.
• k == n 은 내 위치가 리프노드임을 의미한다. 따라서 상태 (P)를 출력한다.
• include[k] = false과 powerSet(k + 1) 은 왼쪽 자식 노드로 이동하는 것을 말한다.