Sorting Algorithms

1. Bubble Sort

• (1, 2), (2, 3), (3, 4), ... , (n-1, n) 순서로 큰 값이 bubble되어 배열의 맨 끝에 도착한다.

• 그것을 제외하고 반복하며 배열이 정렬된다.

• O(n^2)

2. Selection Sort

• 배열의 맨 끝과 1, 2, ... , n-1 중 값이 큰 경우에 swap하며 비교한다.

• 그것을 제외하고 반복하며 배열이 정렬된다.

• O(n^2)

3. Insertion Sort

• 배열의 맨 앞부터 비교할 대상을 집는다.

• 배열의 맨 뒤에서 부터 shift하며 알맞은 위치에 insert한다.

• 다음 대상을 집는다.

• O(n^2)

배열의 앞부터 insert 위치를 찾으면, 나머지를 shif 연산시키는 추가 작업이 발생한다. 따라서 비효율적이다.

Insertion Sort는 최약의 경우에 시간 복잡도가 O(n^2)이지만, Bubble Sort와 Selection Sort는 모든 경우에 시간 복잡도가 O(n^2)이다.

4. Merge Sort

• 배열을 반으로 나눈다.

• 각각 정렬한다.

• 정렬된 두 배열을 합치면서 정렬한다.

• O(n * log(n))

Time Complexity: T(n) = 2T(n / 2) + n

🤲 분할 정복법

하나의 문제를 "동일한" 작은 문제들로 분할 -> Recursion으로 해결 -> Combine

: 분할 후 병합할 때 더욱 간단해지는 문제들이 분할 정복법을 사용하기에 적절하다.
: 그래프 노드들을 각각 다른 색으로 색칠하는 문제의 경우 두 가지의 분할된 해결법을 합쳐서 하나의 해결법으로 만드는 방법을 찾는 것이 어렵다. 즉, 이전의 단계가 도움이 되지 않는다.

❗merge 함수의 indexing에 주의하자

📁 merge 과정에서 추가 배열이 필요하다.

int sorted[1000000];

void merge(int* data, int start, int mid, int end) {
	int m = start, n = mid + 1, k = start;

	while (m <= mid && n <= end) {
		if (data[m] < data[n]) {
			sorted[k] = data[m];
			k++;
			m++;
		}
		else {
			sorted[k] = data[n];
			k++;
			n++;
		}
	}

	while (m <= mid) {
		sorted[k] = data[m];
		k++;
		m++;
	}

	while (n <= end) {
		sorted[k] = data[n];
		k++;
		n++;
	}
	
	for (int i = start; i < k; i++) {
		data[i] = sorted[i];
	}
}

void mergeSort(int* data, int start, int end) {
	if (start < end) {
		int mid = (start + end) / 2;

		mergeSort(data, start, mid);
		mergeSort(data, mid + 1, end);

		merge(data, start, mid, end);
	}
}

5. QuickSort

• pivot을 선택한다.

• pivot을 기준으로 왼쪽은 pivot보다 작은 값들, 오른쪽은 큰 값들로 나눈다.

• Worst Case: O(n^2)
  : 이미 정렬된 데이터와 마지막 원소를 pivot으로 선택할 경우

• Best Case: O(n * log(n))
  : 항상 절반으로 분할되는 경우

• Average Case: O(n * log(n))

Merge Sort와 다르게 합병이 필요없다.

• Partition 함수

int partition(int* data, int p, int r) {
	int pivot = data[r];

	int i = p -1; 
	int j = p; // set to p in order to check the next element of j
	while (j < r) {
		if (data[j] >= pivot) {
			j++;
		}
		else {
			i++;
			swap(&data[i], &data[j]);
			j++;
		}
	}

	for (int k = r; k > i + 1; k--) {
		data[k] = data[k - 1];
	}

	data[i + 1] = pivot;
	return i + 1;
}

💡 필요한 아이디어

1. 변수 i 와 j
: i는 pivot 왼쪽 부분의 마지막 index를, j는 검사 할 index (pivot 오른쪽 부분의 마지막 + 1)를 나타낸다.

2. data[i]와 data[j]의 Swap
: 이 Division은 pivot 데이터와 크기 비교만으로 부터 이루어지므로, Sorting에 비해 상대적으로 자유롭게 Swap이 가능한 점을 이용해야 한다.

6. Heap Sort

• Merge Sort와 다르게 추가 배열이 불필요하다.

• Binary Heap 자료구조를 이용한다.

Binary Heap

• Complete Binary Tree는 일차원 배열을 통해 표현이 가능하다.
• Heapify 함수를 통해 Max Heap Property를 만족시켜야 한다.

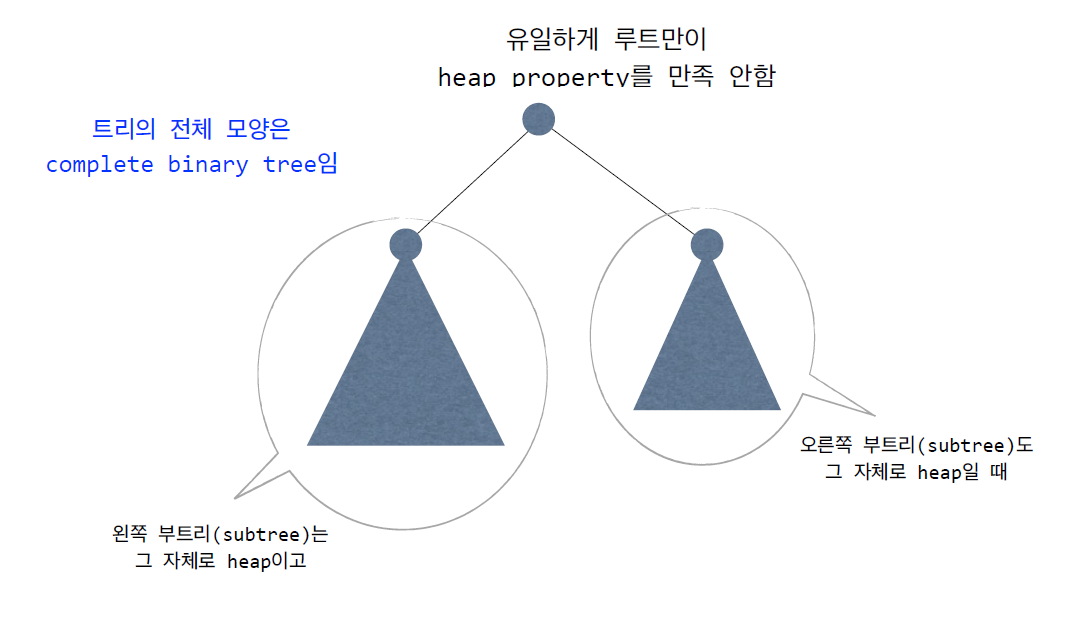
Max Heapify

• 조건: 왼쪽과 오른쪽의 Subtree들이 Max Heap Property를 만족해야 한다.

• Psuedo Code

MAX-HEAPIFY(A, i)
{
if there is no child of A[i]
return;
k ← index of the biggest child of i;
if A[i] ≥ A[k]
return;
exchange A[i] and A[k];
MAX-HEAPIFY(A, k);
}

• O(log(n))
  : 최악의 경우에 Binary Heap의 높이만큼 연산이 발생한다.

🔑 Heapyfiy의 역할
: 해당 노드의 값을 알맞은 위치로 옮긴다.
: 전체 Binary Heap을 Max Heap으로 만들어주는 것이 아님.

Build Heap

void build_max_heap(int* data, int p_idx, int n) {
	// data[n/2] is the last node that has children
	for (int i = (n - 1) / 2; i >= 0; i--) {
		maxHeapify(data, i, n);
	}
}

• 자식 노드가 있는 마지막 노드에 n / 2의 index로 접근할 수 있다.

• A[n / 2]부터 시작하기 때문에 항상 Max Heapify에 O(log(n))이 걸리지 않는다.

• O(n)

Heap Sort

• Extract Max

• 마지막 노드부터 루트 다음의 노드까지 반복하면 배열이 Sorting 된다.

• Psuedo Code

BUILD-MAX-HEAP(A)
for i ← heap_size downto 2 do
exchange A[1] ↔ A[i]
heap_size ← heap_size - 1
MAX-HEAPFIY(A,1)

• O(n * log(n))