[JS] 분수의 덧셈

문제 - 분수의 덧셈

---

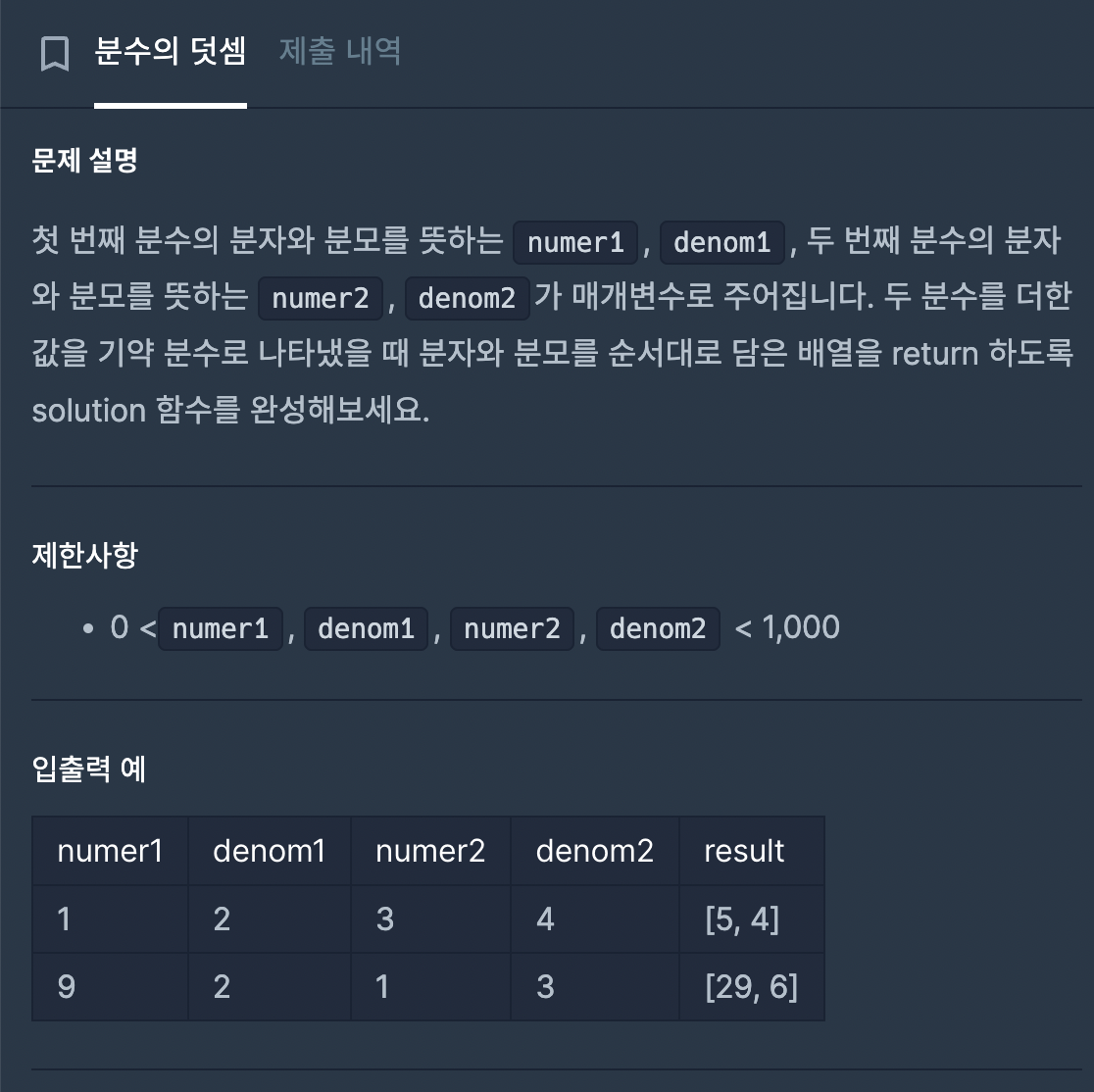
여기서 핵심은 최대공약수를 구하는 것이다!

먼저, 기약분수 상관하지 않고 통분해준다.

function solution(numer1, denom1, numer2, denom2) {
  var answer = [];

  //분모 구하기
  let denom = denom1 * denom2;

  //분자 구하기
  let numer = denom1 * numer2 + denom2 * numer1;
  

그 후 분모와 분수의 최대공약수를 구해 각각 나눠주면 된다!

---

그렇다면 최대공약수는 어떻게 구하는가..?

두가지의 방법이 있다.

첫 번째. 2부터 min(A, B)까지 모든 정수로 나누어보는 방법

let getGCD = (num1, num2) => {
    let gcd = 1;

    for(let i=2; i<=Math.min(num1, num2); i++){
        if(num1 % i === 0 && num2 % i === 0){
            gcd = i;
        }
    }

    return gcd;
}

2. 유클리드 호제법

💡 유클리드 호제법
2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘의 하나이다.
호제법이란 말은 두 수가 서로 상대방 수를 나누어 결국 원하는 수를 얻는 알고리즘을 나타낸다.
2개의 자연수(또는 정식) a,b에 대하여 a를 b로 나눈 나머지를 r이라고 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
이 성질에 따라, b를 r로 나눈 나머지 r'을 구하고, 다시 r을 r'으로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 대 나누는 수가 a와 b의 최대공약수다.

이해가 잘 안되는가? 나도 그랬다.. 이 말만 보았을 땐

진심 이랬음 근데 그냥 숫자를 넣어서 생각해보자.

만약 35와 42의 최대공약수를 구한다고 해보자.

큰 수 72(a)를 35(b)로 나누면

42 / 35 = 1 ... 7
즉, 42 = 35 * 1 + 7

이때 나머지가 0이 아니므로 나눈수(35)를 나머지(7)로 다시 나눈다.

35 / 7 = 5 ... 0
즉, 35 = 7 * 5

나머지가 0이 되었다. 이때 나누는 수였던 7이 최대공약수가 되는 것이다.

---

이제 최대공약수 구하는 것을 코드로 구현해보면 다음과 같다.

let getGCD = (a, b) => (b > 0 ? getGCD(b, a % b) : a);

따라서 분수 구하기의 전체 코드는

function solution(numer1, denom1, numer2, denom2) {
  var answer = [];

  //분모 구하기
  let denom = denom1 * denom2;

  //분자 구하기
  let numer = denom1 * numer2 + denom2 * numer1;

  //최대 공약수구하기
  //최대 공약수: 두 수의 공통된 약수 중에서 가장 큰 정수
  //구하는 방법: 유클리드 호제법

  let getGCD = (a, b) => (b > 0 ? getGCD(b, a % b) : a);
  let gcd = getGCD(numer, denom);

  //최대 공약수를 분자, 분모에 나누고 배열에 넣기
  answer[0] = numer / gcd;
  answer[1] = denom / gcd;

  return answer;
}

---

참고

• devJade- JavaScript로 최대공약수(GCD), 최소공배수(LCM) 구하기
  https://velog.io/@devjade/JavaScript%EB%A1%9C-%EC%B5%9C%EB%8C%80%EA%B3%B5%EC%95%BD%EC%88%98GCD-%EC%B5%9C%EC%86%8C%EA%B3%B5%EB%B0%B0%EC%88%98LCM-%EA%B5%AC%ED%95%98%EA%B8%B0