[백준] #23247번 Ten (C++)

문제

https://www.acmicpc.net/problem/23247

접근 방식

2021 icpc 인터넷 예선 j번 문제이다.

처음 생각했을 때 무작정 브루트포스 방식으로 더하는 방법밖에 생각나지 않았다. 하지만 m, n 범위가 300이하이므로 좀 더 최적화할 수 있는 방법을 고민하다가 이전에 2차원 누적합 알고리즘으로 풀었던 구간 합 구하기5 (링크) 문제가 떠올랐다.

2차원 누적합으로 먼저 데이터를 전처리한다면 모든 영역의 경우의 수를 구하더라도 부담을 줄일 수 있다. 또한 2차원 누적합 데이터에서 두 좌표만 주어지면 영역의 크기를 구하기 수월해진다.

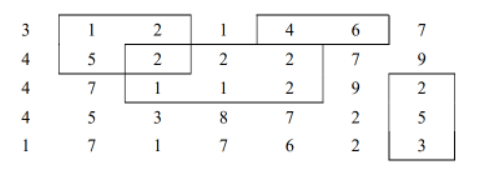
모든 경우의 수를 구하는 방법은 크게 어렵지 않다. 시작점 x1, y1를 두고 끝 점 x2, y2를 이동시키면서 점 4개 영역이 10인지 검사해주면 된다.

하지만 이렇게 무작정 제출을 한다면 시간 초과가 발생하는데 이 역시 O(n^4)이 걸린다.

조금 더 문제를 유심히 살펴보면 테이블의 데이터 값의 범위는 양수이다. 즉, 최솟값인 '1'만 채워져 있다 가정하더라도 모든 경우의 수를 생각할 필요 없이 계산 도중 10을 초과하면 해당 영역의 loop문에서 빠져나오면 된다는 것이다.

코드

#include<bits/stdc++.h>
using namespace std;

int m, n;
int rec[301][301];
int sum[301][301];

int main() {
	cin >> m >> n;

	for (int i = 0; i < m; i++) {
		for (int k = 0; k < n; k++) {
			cin >> rec[i][k];
		}
	}

	int ans = 0;

	for (int i = 0; i < m; i++) {
		for (int k = 0; k < n; k++) {
			if (i == 0 && k == 0)
				sum[i + 1][k + 1] = rec[i][k];
			else if (i == 0) {
				sum[i + 1][k + 1] = rec[i][k] + sum[i + 1][k];
			}
			else if (k == 0) {
				sum[i + 1][k + 1] = rec[i][k] + sum[i][k + 1];
			}
			else {
				sum[i + 1][k + 1] = rec[i][k] + sum[i][k + 1] + sum[i + 1][k] - sum[i][k];
			}

		}
	}

	// i ~ h
	// k ~ w 까지 영역의 합


	for (int i = 1; i <= m; i++) {
		for (int k = 1; k <= n; k++) {
			for (int h = i; h <= m; h++) {
				for (int w = k; w <= n; w++) {
					int s = sum[h][w] - sum[h][k - 1] - sum[i - 1][w] + sum[i - 1][k - 1];
					if (s == 10) ans++;
					if (s >= 10) break;

					//cout << sum[h][w] << " " << sum[h][k - 1] << " " << sum[i - 1][w] << " " << sum[i - 1][k - 1] << endl;
					//cout << i << ", " << k << " " << h << ", " << w << " " <<  s << endl;
				}
			}
		}
	}

	cout << ans;
}