
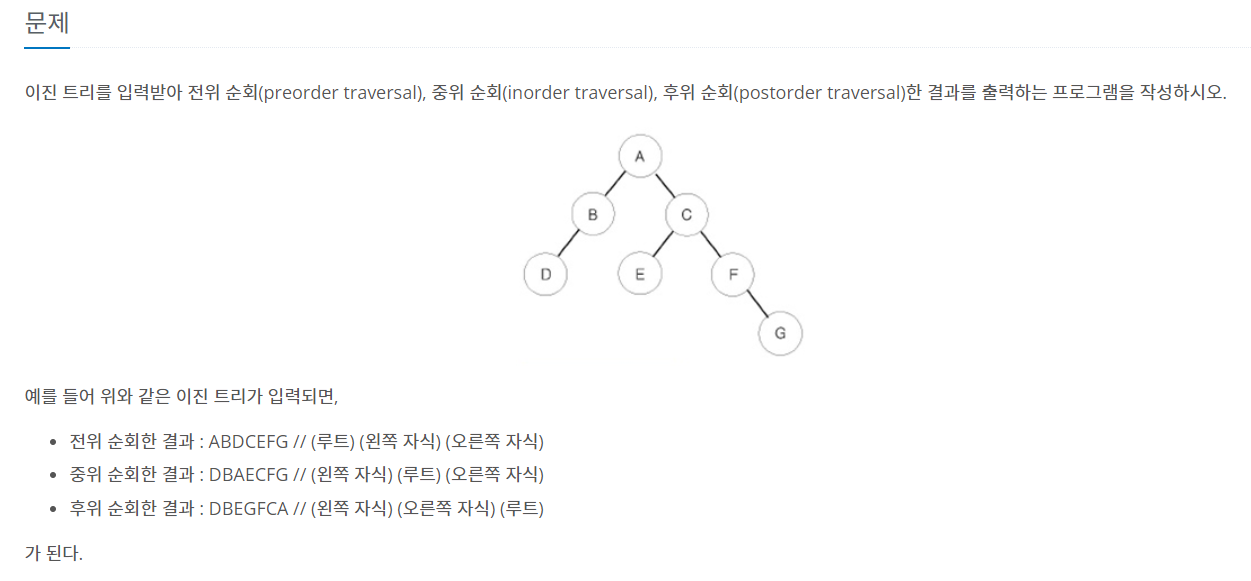
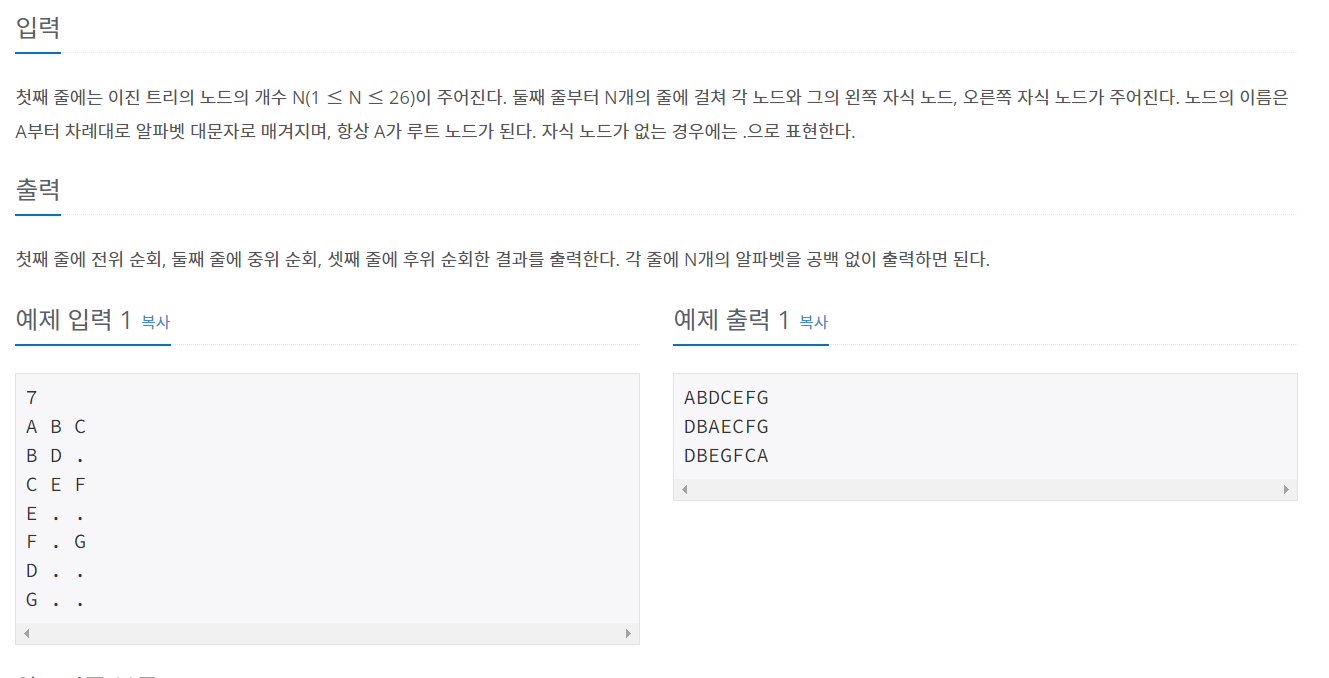
백준 1991번 - 트리 순회 풀이
💡 정답
import sys
N = int(sys.stdin.readline().strip())
tree = {}
for n in range(N):
root, left, right = sys.stdin.readline().strip().split()
tree[root] = [left, right]
def preorder(root):
if root != '.':
print(root, end='') # root
preorder(tree[root][0]) # left
preorder(tree[root][1]) # right
def inorder(root):
if root != '.':
inorder(tree[root][0]) # left
print(root, end='') # root
inorder(tree[root][1]) # right
def postorder(root):
if root != '.':
postorder(tree[root][0]) # left
postorder(tree[root][1]) # right
print(root, end='') # root
preorder('A')
print()
inorder('A')
print()
postorder('A')① Python으로 트리 구현하는 방법 : dictionary(사전) 사용
root를 key로 / left, right 자식들을 value로 할당한다.
tree[root] = left, right
tree = {}
tree["A"] = "B", "C"
이렇게 tree의 인덱스는 KEY로, 저장되는 값은 VALUE로 사전에 저장할 수 있다.
{"A" : ("B","C")}
👉 의미 : A가 부모인 노드가 B, C / A의 자식이 B, C
※ A를 key로 가지는 value인 B를 인덱싱하는 방법 : tree["A"][0]
② 전위 / 중위 / 후위 순회마다 재귀함수 코드의 순서 바꾸기
# 한번 재귀할 때마다 탐색을 한번 더 하는 의미로 받아들이자
# 함수 안의 ~~order(tree[root][0]) 재귀함수는 왼쪽으로 끝까지 탐색한다는 의미
# 함수 안의 ~~order(tree[root][1]) 재귀함수는 오른쪽으로 끝까지 탐색한다는 의미
# root -> 출력하면 됨
# 1. 전위 순회 : 루트 -> 왼쪽 자식 -> 오른쪽 자식이므로 재귀함수 순서도 root출력문 -> 왼쪽 재귀함수 -> 오른쪽 재귀함수
def preorder(root): # 루트 -> 왼쪽 자식 -> 오른쪽 자식 순으로 탐색
if root != '.':
print(root, end='') # root
preorder(tree[root][0]) # left -> left가 새로운 root가 된다.
preorder(tree[root][1]) # right -> right가 새로운 root가 된다.
# 2. 중위 순회 : 왼쪽 자식 -> 루트 -> 오른쪽 자식이므로 재귀함수 순서도 왼쪽 재귀함수 -> root 출력문 -> 오른쪽 재귀함수
def inorder(root): # 왼쪽 자식 -> 루트 -> 오른쪽 자식 순으로 탐색
if root != '.':
# TEST CASE를 예로 들면 B에서 tree[root][0] = "D"이고 D의 tree(root[0]) = "."이 돼서 root인 D를 출력하고 right로 넘어간다.
inorder(tree[root][0]) # left
print(root, end='') # root
inorder(tree[root][1]) # right
# 3. 후위 순회 : 왼쪽 자식 -> 오른쪽 자식 -> 루트이므로 재귀함수 순서도 왼쪽 재귀함수 -> 오른쪽 재귀함수 -> root 출력문
def postorder(root): # 왼쪽 자식 -> 오른쪽 자식 -> 루트 순으로 탐색
if root != '.':
postorder(tree[root][0]) # left
postorder(tree[root][1]) # right
print(root, end='') # root