Tree
이번에는 data structure 중에서 tree에 대해 알아보겠습니다. tree는 기본적으로 linked list와 같이 여러 개의 node들을 연결한 형태를 가지고 있는 data structure입니다. 여기서 tree structure가 되기 위한 몇 가지 rule이 있습니다.
- first node(a.k.a. root node)가 하나 존재한다.
- 각 node는 여러 개의 node를 point할 수 있다.
- root node를 제외한 모든 node는 자신을 가리키는 node를 정확히 한 개 가질 수 있다.
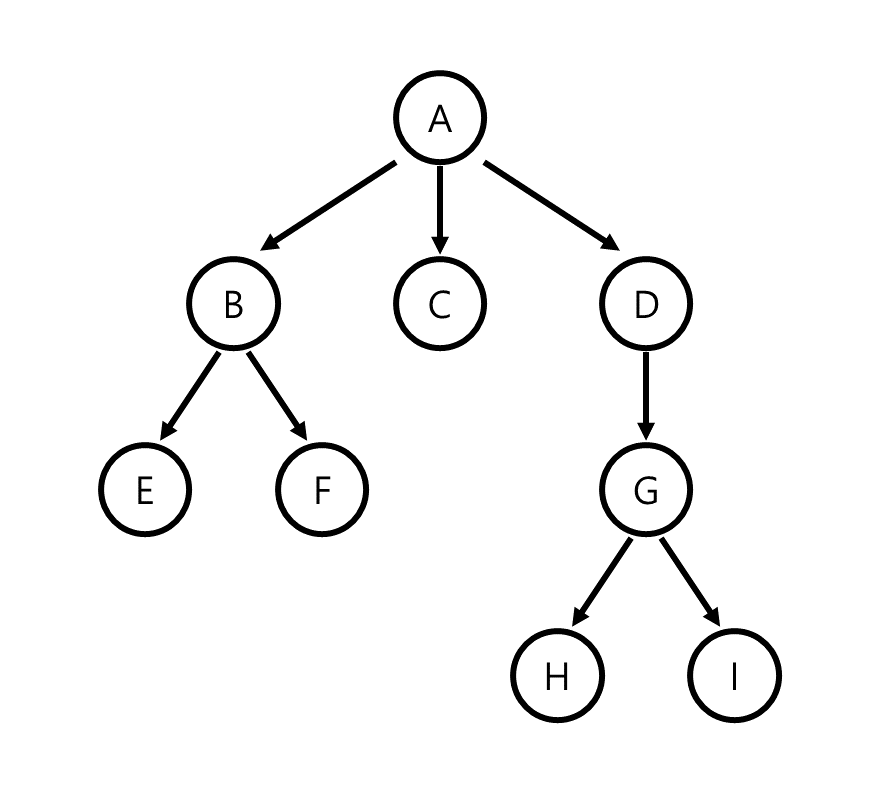
다음 그림은 위의 세 가지 규칙을 모두 만족하는 tree의 예시입니다. A가 위의 정의에서 root node에 해당하며, 각 node가 가리키는 다른 node의 수는 각각 다른 것을 볼 수 있습니다. 또한 A를 제외한 모든 node는 자신을 가리키는 node가 정확히 하나 존재하는 것을 볼 수 있습니다.
- Terminology
tree에 대해 이야기하기 전에 tree에 적용되는 몇 가지 용어에 대해서 살펴볼 필요가 있습니다. 이에 대해서 먼저 알아봅시다.
-
Parent, Children, Sibling
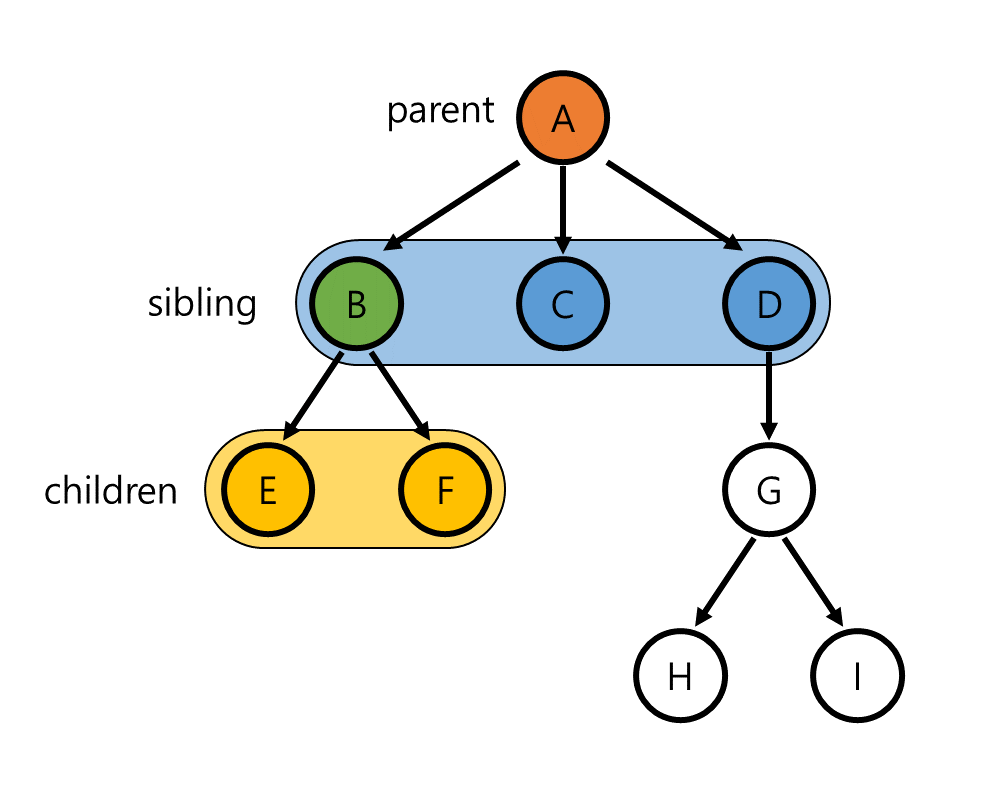
앞선 정의에서 각 node는 여러 node를 point할 수 있고 root를 제외한 모든 node는 자신을 가리키는 node를 오직 하나만 가질 수 있다고 설명했습니다. 여기서 각 node가 가리키는 다른 node들을 children(child) node, 자신을 기리키고 있는 node를 parent node라 합니다. 또한 동일한 parent를 가지고 있는 node들을 sibling이라 합니다. 아래 그림은 node B의 parent, children, sibling을 각각 표시한 것입니다.
-
Degree
각 node마다 가지고 있는 children의 수를 해당 node의 degree라 합니다. 예를 들어, 위의 그림에서 node A의 degree는 3, node D의 degree는 1이며 node C의 degree는 0입니다. -
Leaf nodes, Internal nodes
node C와 같이 degree가 0인 node를 모두 leaf node라 하고, root node를 포함해 그 외의 node들은 모두 internal node라 합니다. 위의 그림에서는 node C, E, F, H, I가 모두 leaf node이며 node A, B, D, G는 모두 internal node입니다. -
Path, Depth, Height
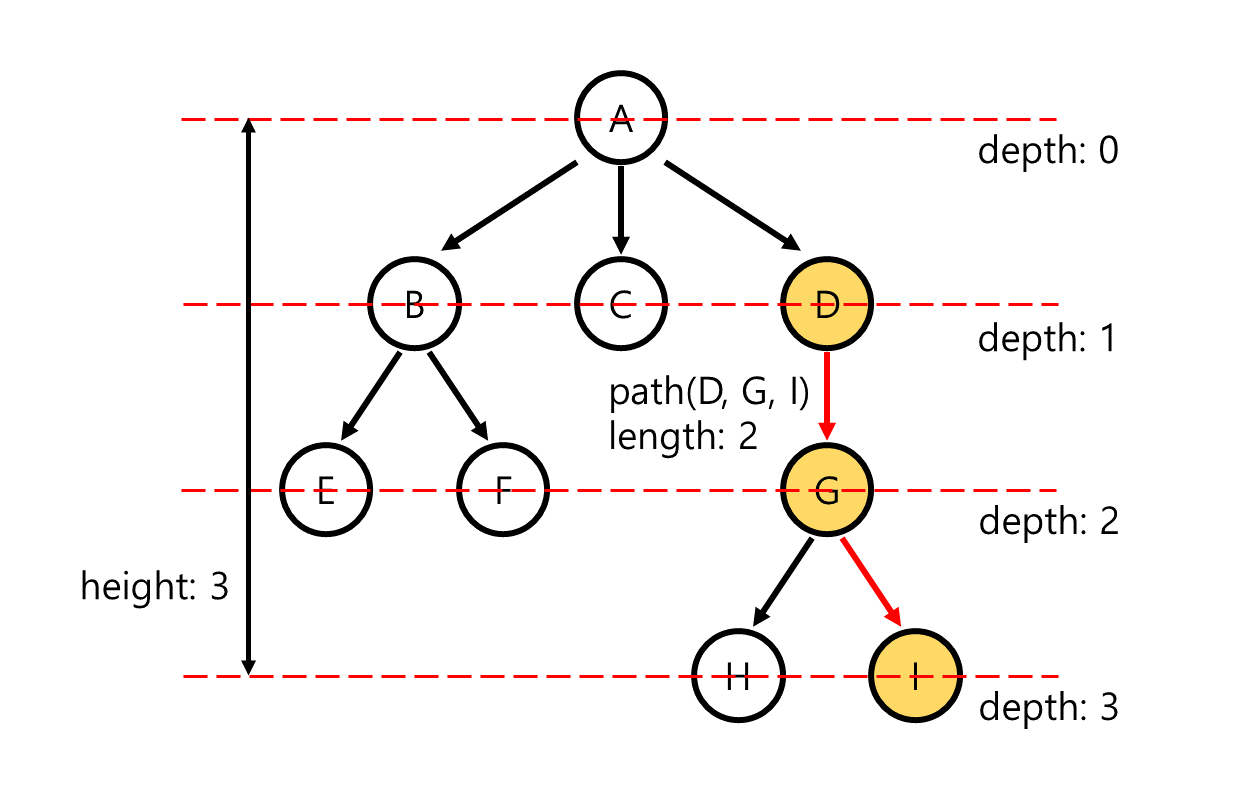
한 node로부터 다른 node까지 자신의 child만을 point하면서 이동할 수 있는 경로가 존재하는 경우, 이를 두 node 사이의 path라 한다. 예를 들어, 위의 tree에서 node D와 node I의 경우 D G I로 child를 pointing하며 이동하는 path가 존재합니다. path는 존재하지 않거나 유일하게 존재하며, 예시의 경우 (D, G, I)의 sequence를 제외하고는 다른 path가 존재하지 않습니다. 또한 path에서 다른 node를 찾아 이동하는 횟수를 path의 length라 하며 위의 예시는 length가 2입니다. 또한 자기 자신으로 향하는 path의 경우 그 length는 0으로 정의합니다.
root node는 항상 다른 node로 향하는 path가 unique하게 존재합니다. root에서 임의의 node X로 향하는 path를 찾을 때 해당 path의 length를 X의 depth라 합니다. 예를 들어 위의 tree에서 node E는 root로부터 (A, B, E)의 path를 통해 찾을 수 있으므로 node E의 depth는 2입니다.
모든 node의 depth를 구했을 때 depth들의 maximum을 구할 수 있을 것입니다. depth의 maximum value를 해당 tree의 height로 정의합니다. 위의 tree는 maximum depth가 node H, I에서 3이므로 height 3의 tree입니다. 단일 node만으로 구성된 tree의 경우 자기 자신으로 향하는 path의 length가 0이므로 해당 tree는 height가 0입니다.
-
Ancestor, Descendent
두 node X, Y에 대해 X에서 Y로 향하는 path가 존재하는 경우 X를 Y의 ancestor, Y를 X의 descendent라 합니다. 예를 들어, 위의 tree에서 path (D, G, I)의 경우 D는 I의 ancestor이며 I는 D의 descendent입니다. 정의에 의해 자기 자신으로 향하는 path의 경우 자기 자신이 ancestor이자 descendent가 됨을 알 수 있습니다. 이를 피하기 위해 자기 자신을 ancestor 또는 descendent group에서 제외하는 strict ancestor, strict descendent를 정의하기도 합니다. -
Subtree
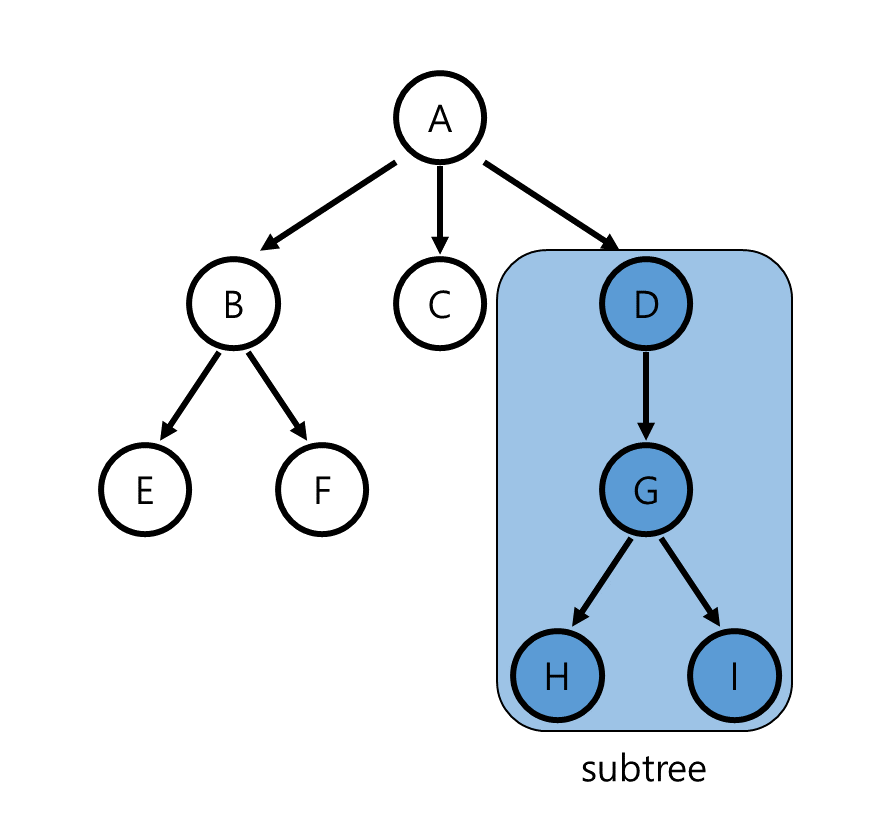
임의의 node X에 대해서, 해당 node와 그 node의 모든 descendent를 모은 것은 X를 root로 하는 하나의 tree를 형성합니다. 이와 같이 tree의 어떤 node를 root로 해 모든 descendent를 포함하는 tree를 subtree라 합니다. 위의 tree에서는 node D를 root로 했을 때 그 descendent인 node G, H, I를 포함하는 tree가 하나의 subtree가 될 수 있습니다.
- Implementation of abstract tree
다른 tree들을 알아보기 이전에 먼저 abstract tree를 code로 구현해보도록 하겠습니다. abstract tree는 다음 요소들을 포함하고 있습니다.
- value
- pointer of parent node
- pointers of children nodes in linked list
따라서, tree class의 definition은 다음과 같습니다.
template <typename T>
class SimpleTree {
public:
SimpleTree(T const& = T(), SimpleTree *= nullptr);
T get_value() const;
SimpleTree<T> *get_parent() const;
int get_degree() const;
bool is_root() const;
bool is_leaf() const;
SimpleTree<T> *get_child(int n) const;
SimpleTree<T> *attach(T const &obj);
int size() const;
int height() const;
private:
T value;
SimpleTree *parent;
List<SimpleTree *> children;
};define해야 할 함수가 많기 때문에 나누어 작성하도록 하겠습니다. 먼저 비교적 간단하게 구현할 수 있는 is_leaf() 함수까지의 구현을 먼저 살펴보겠습니다.
template <typename T>
SimpleTree<T>::SimpleTree(T const &obj, SimpleTree *p)
: value(obj), parent(p) {
// empty constructor
}
template <typename T>
T SimpleTree<T>::get_value() const{
return value;
}
template <typename T>
SimpleTree<T> *SimpleTree<T>::get_parent() const{
return parent;
}
template <typename T>
int SimpleTree<T>::get_degree() const{
return children.size();
}
template <typename T>
bool SimpleTree<T>::is_root() const{
return get_parent() == nullptr;
}
template <typename T>
bool SimpleTree<T>::is_leaf() const{
return get_degree() == 0;
}위의 function들은 모두 class에서 정의한 member variable을 return하거나 function call의 결과를 활용해 간단하게 구현할 수 있습니다. 다음으로 구현이 까다로울 수 있는 부분인 children node를 찾고 child를 attach하는 function을 보겠습니다.
template <typename T>
SimpleTree<T> *SimpleTree<T>::get_child(int n) const {
if (n < 0 || n >= get_degree()) return nullptr;
auto it = children.begin();
for (int i = 1; i < n; ++i) ++it;
return *it;
}
template <typename T>
SimpleTree<T> *SimpleTree<T>::attach(T const &obj) {
auto child = new SimpleTree(obj, this);
children.push_back(child);
return child;
}child를 find할 때 child pointer가 linked list의 형태로 저장되어 있으므로 loop를 활용해 iterator를 찾아 return하는 방식으로 구현한 것을 볼 수 있습니다. 또한 child를 attach하는 것도 새로운 node를 만들어 이를 linked list에 push하는 것으로 구현할 수 있습니다. tree의 size와 height를 구하는 function은 다음 topic에 대한 설명을 이어나간 다음에 다시 돌아와 살펴보겠습니다.
Tree traversal
tree structure를 활용할 때 tree 내의 모든 object를 search해야 하는 경우가 자주 있을 것입니다. 그러기 위해서는 tree에서 linked list의 형태로 저장되어 있는 child들을 효율적으로, 그리고 빠짐없이 search하는 algorithm이 필요할 것입니다. 이번에는 tree의 object를 search하는 두 가지 방법에 대해서 살펴보도록 하겠습니다.
- Breadth-first traversal
breadth-first traversal, 한국어로 너비 우선 탐색은 한 node의 모든 child를 먼저 search한 후 child node들의 child를 탐색하도록 구현한 algorithm입니다. 즉, depth가 0인 node(root node)를 시작으로 depth가 1, 2, ..., 인 node를 차례대로 탐색해 나가는 방법을 사용합니다.
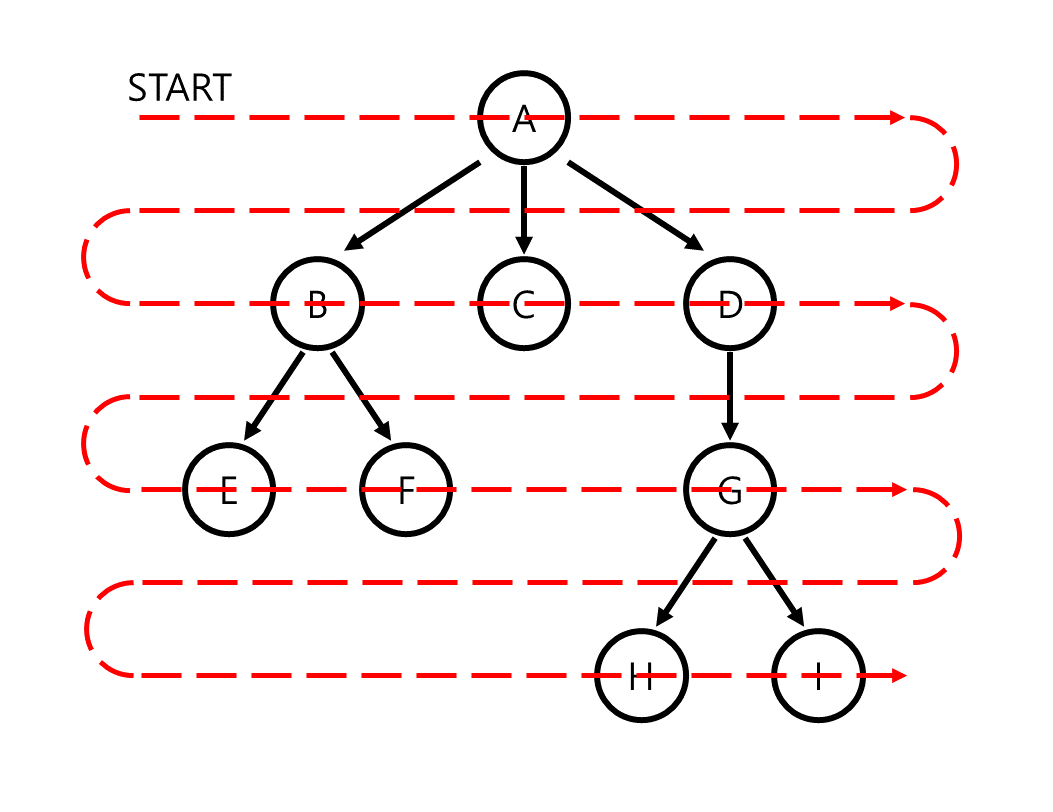
breadth-first traversal은 queue를 활용하면 쉽게 구현이 가능합니다. root node를 시작으로 한 node를 방문할 때 그 node의 모든 children을 queue에 push합니다. 모든 children을 push한 후 해당 node에 대한 search가 끝나면 다음으로 search할 node를 queue의 front node로 선택합니다. 이 algorithm은 depth k의 node를 search할 때 모든 depth +1의 node를 push하게 하고 결국 depth k의 모든 node를 search한 후에 depth +1의 node를 search하도록 만듭니다.
- Depth-first traversal
depth-first traversal, 한국어로 깊이 우선 탐색은 node의 한 child를 root로 하는 subtree를 모두 search한 후에 그 다음 child를 root로 하는 subtree를 모두 search하는 것을 반복하는 방법입니다. 즉, root를 시작으로 leaf node에 도달할 때까지 child 하나를 방문하는 것을 recursive하게 반복하며 search를 진행합니다. 이러한 algorithm을 backtracking이라 합니다.
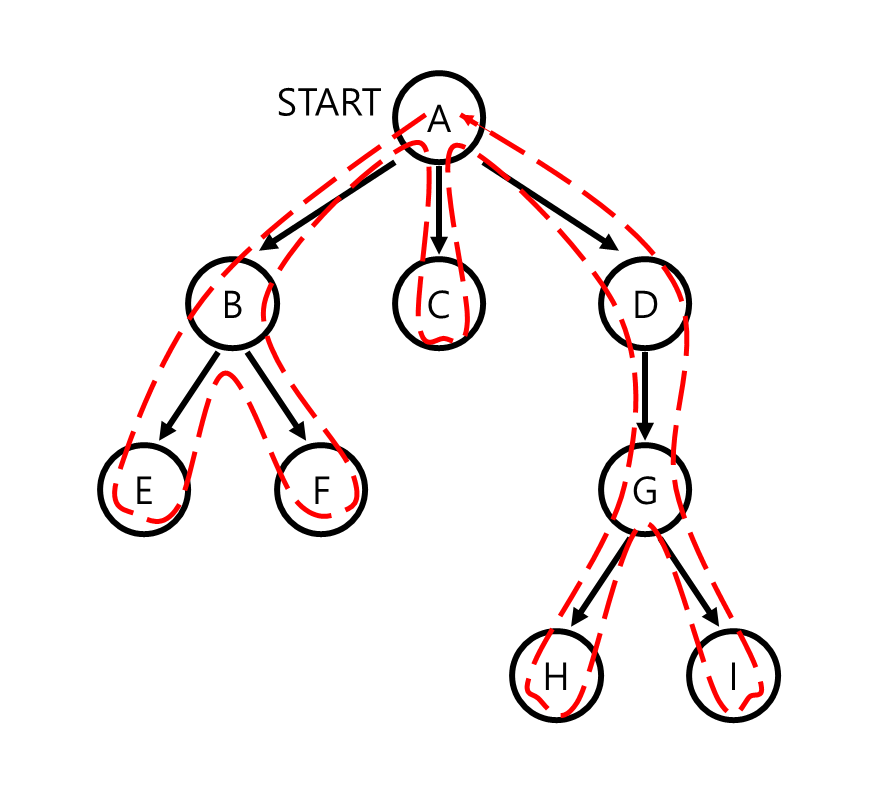
depth-first traversal은 recursive function을 통해 구현할 수 있습니다. node에서 각 child에 access할 때마다 function을 recursive하게 실행해 해당 child의 하위 child를 search할 수 있도록 구현하면 위의 그림과 같은 순서대로 search가 가능합니다. 혹은 stack을 활용하여 child를 모두 stack에 push하고 stack의 top에 access하는 형태로도 구현할 수 있다. stack의 특성으로 인해 항상 child 하나를 root로 하는 subtree를 모두 탐색하기 전에는 다른 child를 탐색할 수 없게 되어 depth-first search가 가능해진다.
breadth-first와 depth-first 모두 node를 각각 한 번씩만 search하게 되므로 time complexity는 이 된다. 하지만 space complexity에는 차이가 있는데, breadth-first search는 어떤 depth 에 해당하는 node가 매우 많아진다면 이를 모두 queue에 push해야 하기 때문에 그만큼의 memory가 필요해진다. 따라서 node가 가장 많은 depth의 node 수를 이라 하면 의 space complexity를 가진다. depth-first search의 경우 한 node에서 항상 다음 depth의 node를 search하고 다시 돌아오기 전까지는 이를 memory에 저장해야 하므로 tree의 height만큼의 data를 저장해야 한다. 따라서 height가 인 tree의 경우 의 space complexity를 가진다.
- Recall: Implementation of abstract tree
앞에서 구현한 abstract tree에서 tree의 size와 height를 구하는 function을 살펴보겠습니다. 아래의 code가 size와 height를 구하는 function의 implementation 예시이며, 두 code 모두 depth-first search로 구현되어 있습니다.
template <typename T>
int SmipleTree<T>::size() const{
int tree_size = 1;
for (auto child = children.begin(); child != children.end(); child++) {
tree_size += (*child)->size();
}
return tree_size;
}
template <typename T>
int SimpleTree<T>::height() const{
int tree_height = 0;
for (auto child = children.begin(); child != children.end(); child++) {
tree_height = std::max(tree_height, 1 + (*child)->height();
}
return tree_height;
}reference
"Data Structure & Algorithm Analysis in C++", 4th ed, Pearson, M. A. Weiss
