[알고리즘] 소수 구하기 _ 에토체

소수는 1과 자기자신외에 약수가 존재하지 않는 수입니다.
소수 구하기는 에라토스테네스의 체를 사용합니다.

에라토스테네스의 체 원리

1. 구하고자 하는 소수의 범위만큼 1차원 배열을 생성
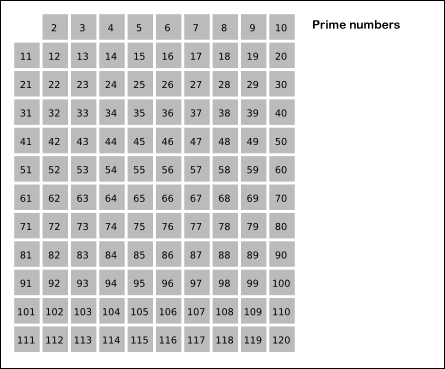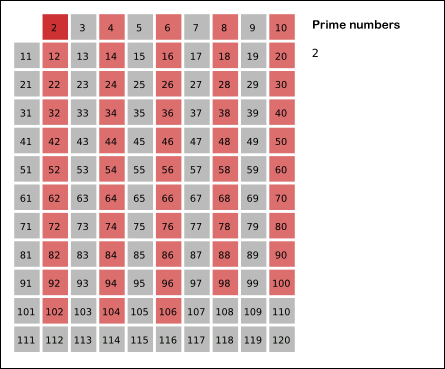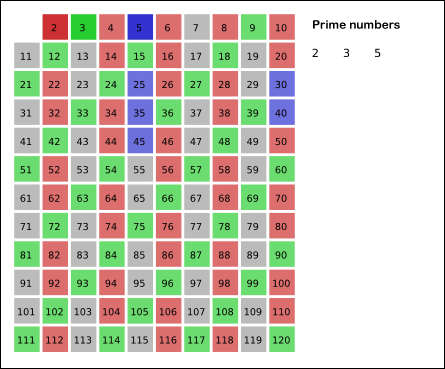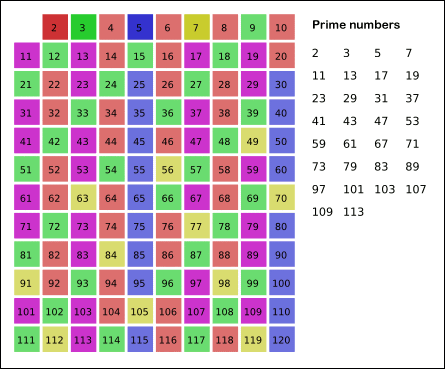
2. 2부터 시작하고, 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지운다.
   --> 이때, 이전에 지워졌던 수, 즉, 처음으로 선택된 수는 지우지 않는다.
3. 배열의 끝까지 순서 2번을 반복한 후 배열에서 남아있는 모든 수를 출력한다.
   

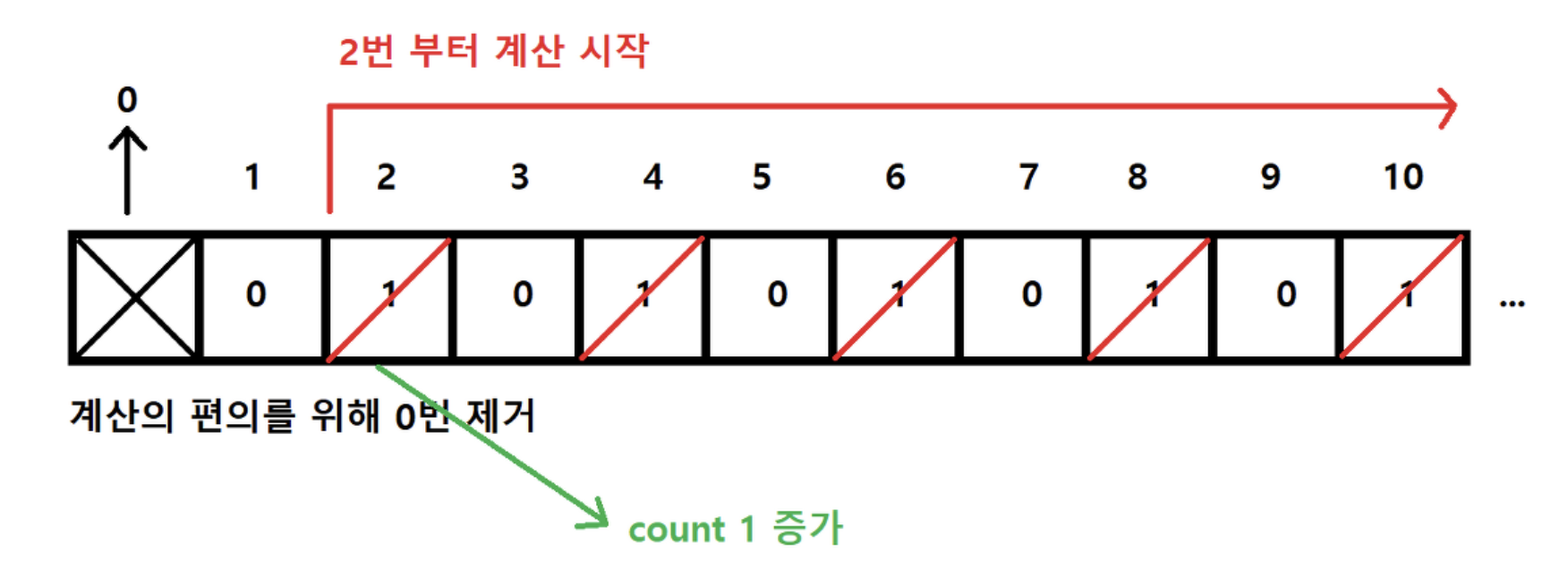
• 위 그림의 코드

ublic int solution(int n) {
    int count = 0;
 
    // n+1 크기 만큼 생성 1부터 n까지의 인덱스로 접근할 수 있음
    int[] nums = new int[n+1];
 
    // 2 번 인덱스부터
    for (int i=2; i<nums.length; i++) {
 
        // 1이면 이미 제외된 숫자
        if (nums[i] == 0) {
            count++;
            for (int j = i; j<nums.length; j+=i) {
                // i의 배수가 1이 아닐 경우만 1로 변경
                if (nums[j] != 1) {
                    nums[j] = 1;
                }
            }
        }
    }
    return count;
}

시간복잡도

이중 for 문을 사용해서, 보통 시간복잡도는 O(N^2)으로 알고 계신분들이 많습니다.
BUt, 실제 시간복잡도는 최적화의 정도에 따라 다르겠지만, 일반적으로 O(Nlog(logN))입니다.
--> 왜? --> 위에 에토체의 원리중 2번을 확인하시면 됩니다.
이전에 지워졌던 수는 지우지 않기 때문에 그만큼 줄어듭니다.

에토체에서, N의 제곱근까지만 탐색하는 이유

N이 ab라고 가정했을 때, a와 b 모두 N의 제곱근보다 클 수 없기 때문입니다.
N = ab 의 a*b가 루트 N 보다는 절대 클 수 없기 때문입니다.
따라서, N의 제곱근까지만 확인해도 전체 범위의 소수를 판별할 수 있습니다.

코드

자바언어입니다.

import java.util.Arrays;

public class SieveOfEratosthenes {
    public static void main(String[] args) {
        int n = 100; // 찾고자 하는 소수의 범위
        boolean[] primeNumbers = sieveOfEratosthenes(n);

        for (int i = 2; i <= n; i++) {
            if (primeNumbers[i]) {
                System.out.print(i + " ");
            }
        }
    }

    public static boolean[] sieveOfEratosthenes(int n) {
        boolean[] primeNumbers = new boolean[n + 1];
        Arrays.fill(primeNumbers, true);
        primeNumbers[0] = false;
        primeNumbers[1] = false;

        for (int i = 2; i * i <= n; i++) {
            if (primeNumbers[i]) {
                for (int j = i * i; j <= n; j += i) {
                    primeNumbers[j] = false;
                }
            }
        }

        return primeNumbers;
    }
}

이 코드는 sieveOfEratosthenes라는 메서드를 사용하여 에라토스테네스의 체를 구현한 것입니다.
main 메서드에서는 이 방법을 사용하여 2부터 n까지의 소수를 출력하게 됩니다.
여기서 n은 찾고자 하는 소수의 범위로 지정할 수 있습니다.
즉, 위 예제에서는 n을 100으로 설정하여 100 이하의 소수를 찾습니다.