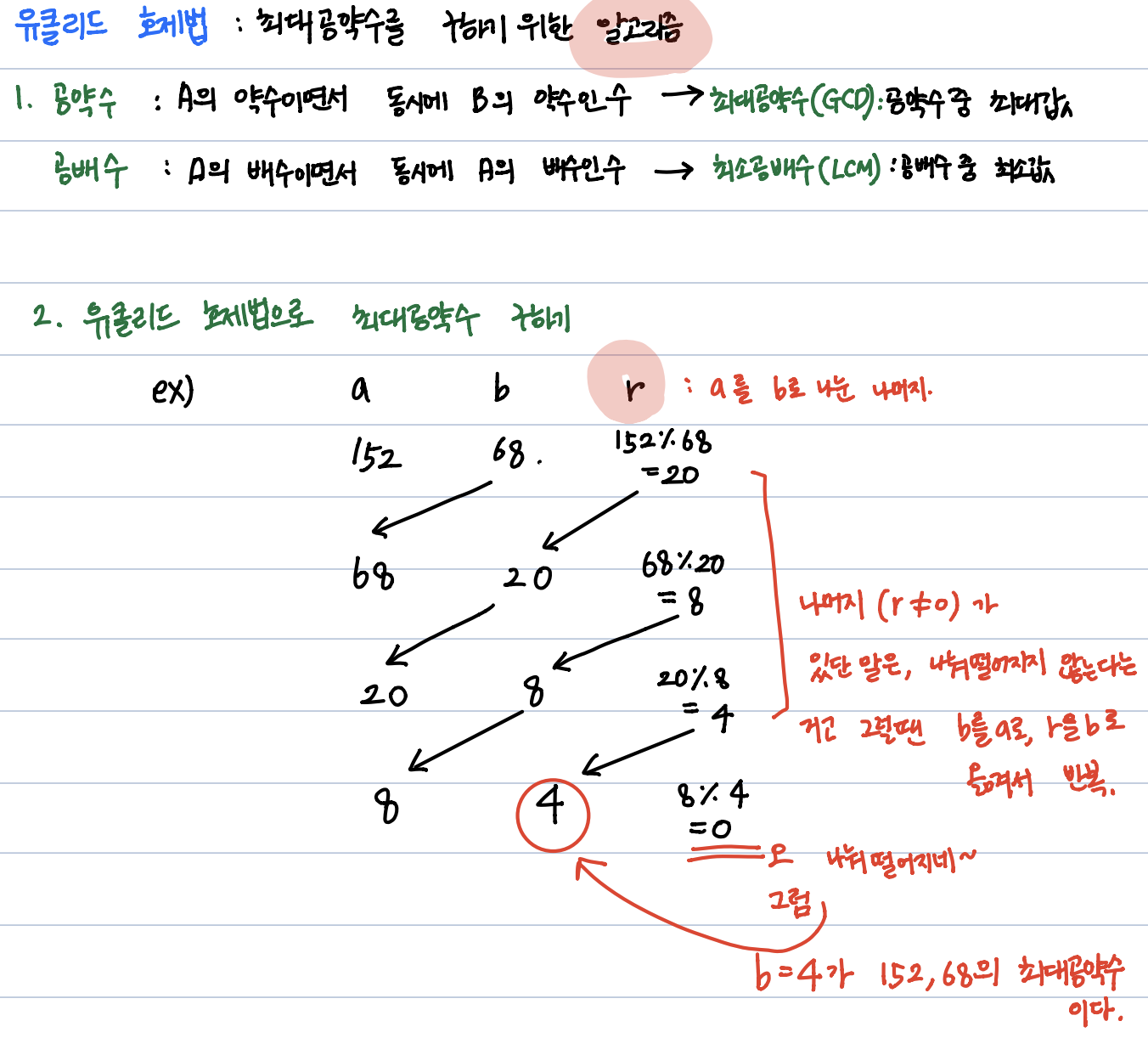
유클리드 호제법이란
두 수의 최대공약수를 구하는 알고리즘입니다.
보통 수리영역을 공부하셨을때, 소인수분해를 이용하여 공통된 소수들의 곱으로 표현하였지만, 컴퓨터에서는 해당 방법으로 구하는 것보다 좀 더 간결하게 유클리드 호제법으로 표현가능합니다.
핵심이론
MOD 연산이 최대 공약수를 구하는 핵심이라서, MOD 연산을 이해하고 있어야 합니다.
10 MOD 4 = 2 // 즉, 10 % 4 = 2이해하기 어려우시다면, % 기호다. 라고 생각하셔도 무방합니다.
유클리드의 호제법은 3단계로 구현됩니다.
- 큰 수를 작으수로 나누는 MOD 연산 수행
- 결과값으로 MOD 연산 수행
- 나머지가 0이 되는 순간의 둘 중 작은 수를 최대 공약수로 선택
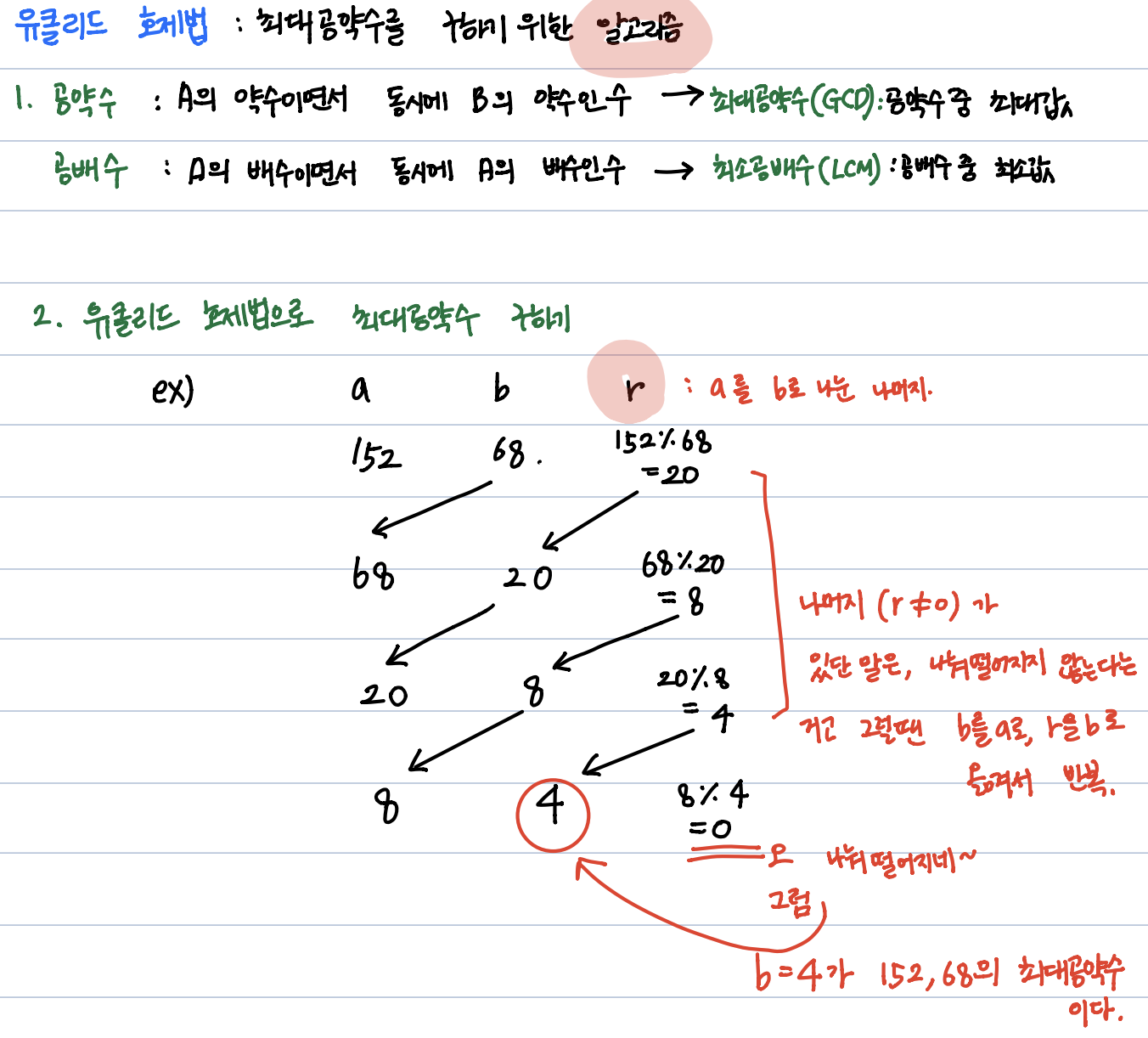
참고로,

예시
gcd(270,192)
270 % 192 = 78
--> 192 % 78 = 36
--> 78 % 36 = 6
--> 36 % 6 = 0
--> 따라서, gcd(270,192) = 6 이 최대공약수.code
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int x = Integer.parseInt(br.readLine());
int y = Integer.parseInt(br.readLine());
int result = GCD(x, y);
System.out.println(result);
}
private static int GCD(int x, int y) {
if(y == 0)
return x;
else
return GCD(y, x % y);
}
}이미지 출처 해당 링크에서 고등학생 때, 배웠더 것들이 기억났다.

기억 나시나요 ? 해당 이미지를 보게되면, 파스칼의 삼각형을 볼 수 있습니다.
해당 문제 가끔씩 모의고사 봤을 때, 30번인가? 나왔던 것으로 기억나네요 ㅋㅋ 추억
