차수

1.4 차수

• 알고리즘에서 포인트는 상수무시하며, 가장 큰 차수만 신경쓰면된다.

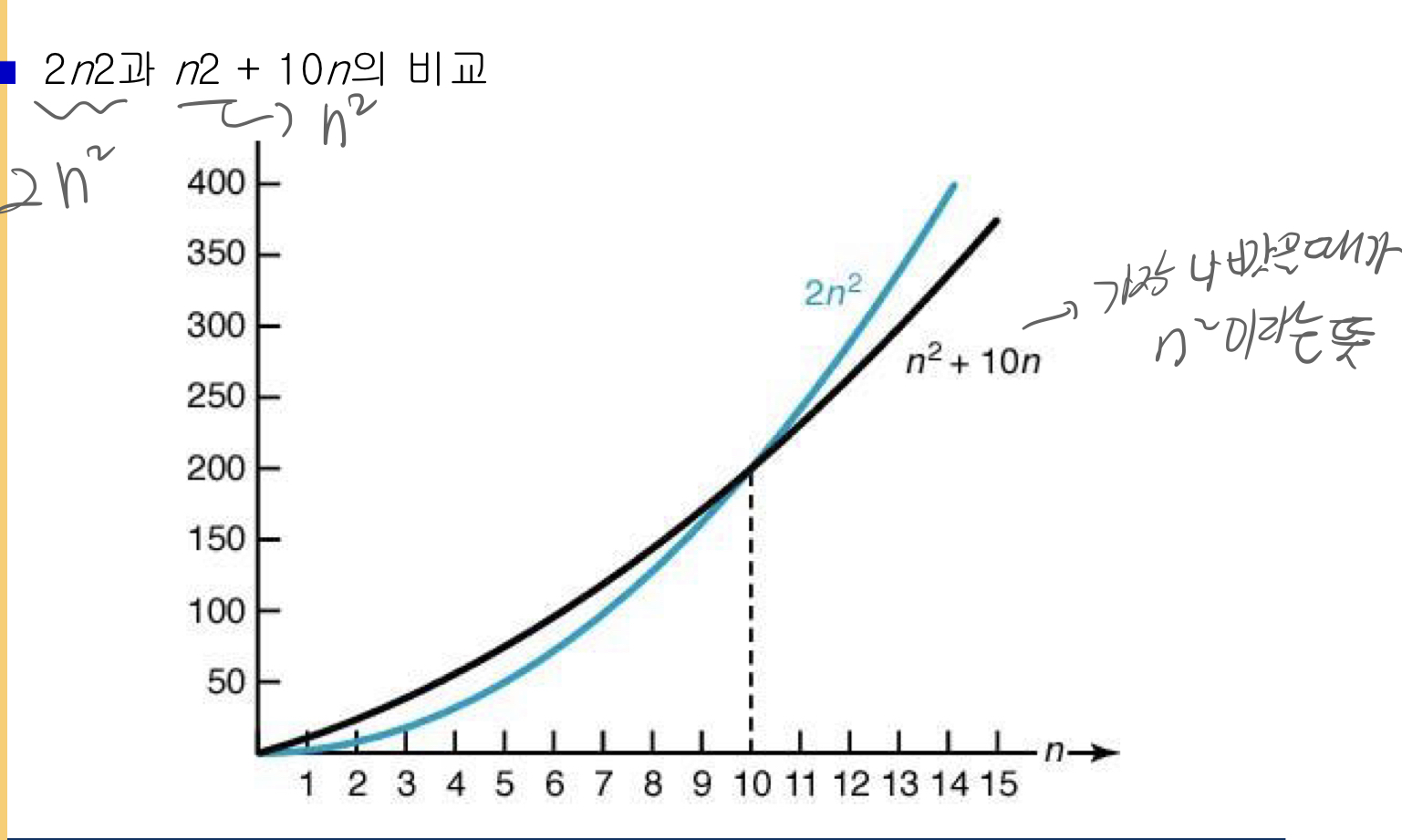
복잡도 함수의 증가율

O (큰 빅O)

(=상한값, 가장 나빳을 때)

O 표기법

어떤 함수 g(n)이 O(n^2)에 속한다는 말은

• 그 함수는 궁극에 가서는 이차함수 cn^2 보다는 작은 값을 가지게 된다는 것을 뜨함. (그래프 상에서는 아래에 위치한다)
• 결론적으로, 그 함수 g(n)은 어떤 2차 함수 cn^2 보다는 궁극적으로 좋다 (기울기가 낮다)

어떤 알고리즘의 시간복잡도가 O(f(n)) 이라면

• 입력된 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 늦어도 f(n)은 된다. ( f(n)이 상환)
• 다시 말하면, 이 알고리즘의 수행시간은 f(n)보다 절대로 더 느릴 수는 없다.
  (느릴 수 없다 = 나빠질 수 없다)
  
  

(1)

(2)

(3)

Ω 표기법

(=빅O에 반대)

• 정의 : 점근적 하한

  

  
  

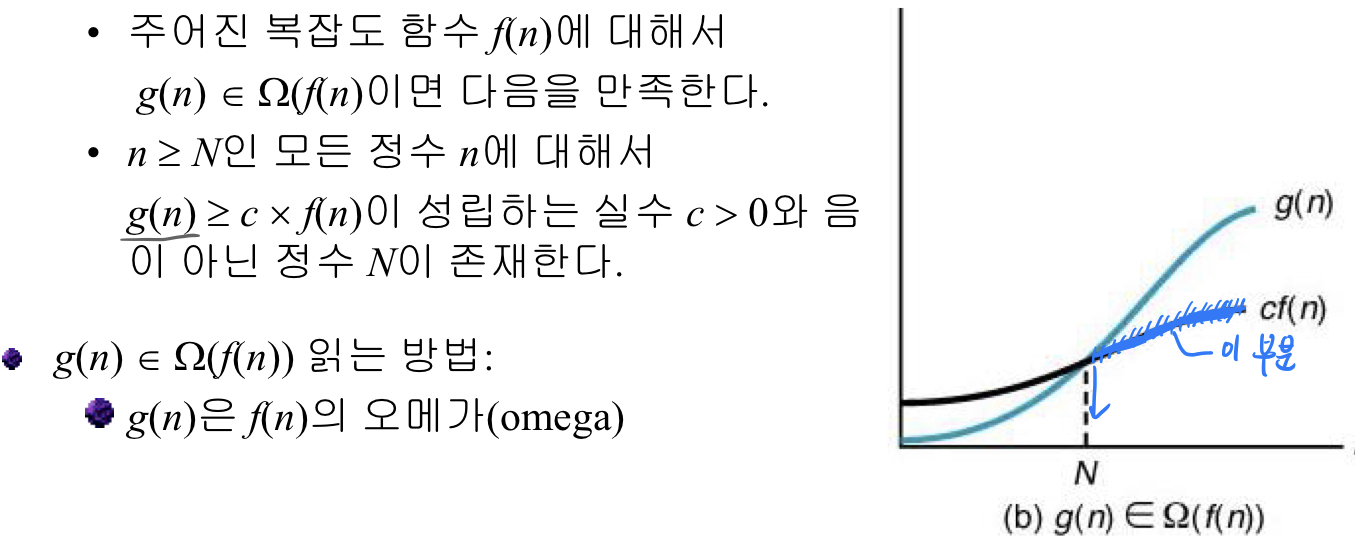
어떤 함수 g(n)이 Ω(n^2)에 속한다는 말은

• 그 함수는 궁극에 가서는 (즉, 어떤 임의의 N값보다 큰 값에 대해서는) 어떤 2차 함수 cn^2의 값보다는 큰 값을 가지게 된다는 것이다. (그래프 상에서 위에 위치)
• 즉, g(n)은 어떤 2차 함수 cn^2 보다는 궁극적으로 나쁘다 (=기울기가 높다)

어떤 알고리즘의 시간복잡도가 Ω(f(n)) 이면,

• 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 빨라도 f(n)밖에 되지 않는다.
  (f(n)이 하한)
• 다시 말하며느 이 알고리즘의 수행시간은 f(n)보다 절대로 더 빠를 수 없다는 말이다.

예시

예시 2

(오메가=가장 좋았을 때임으로)