최적화 기법 Newton's Method, Gradient Descent

Newton's Method

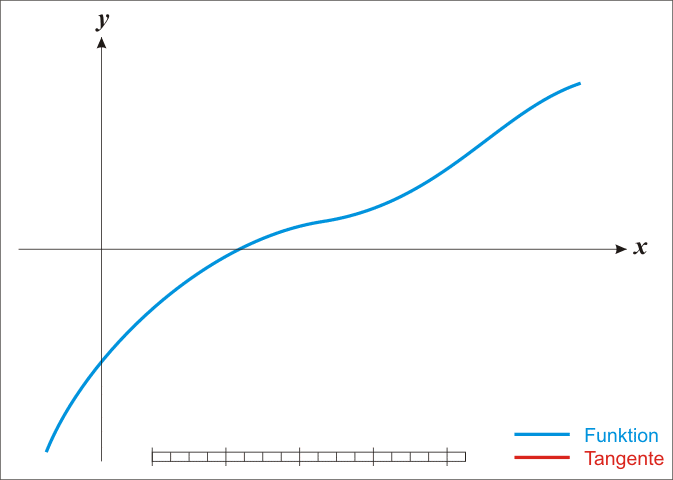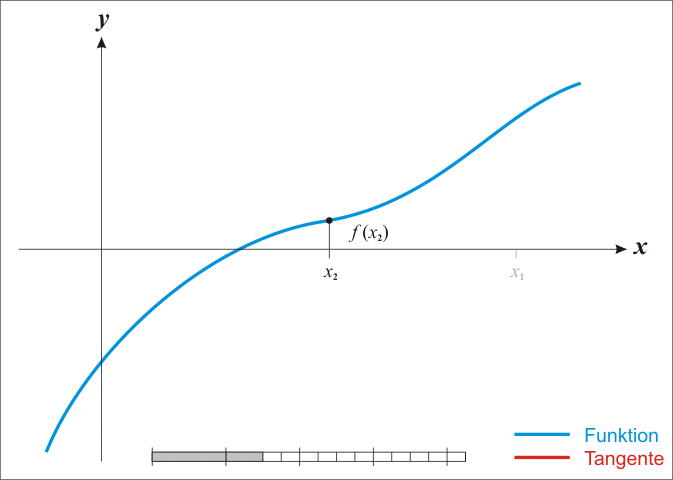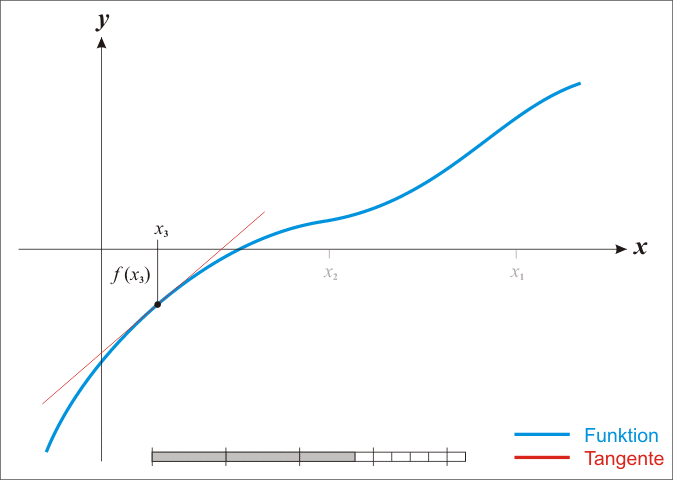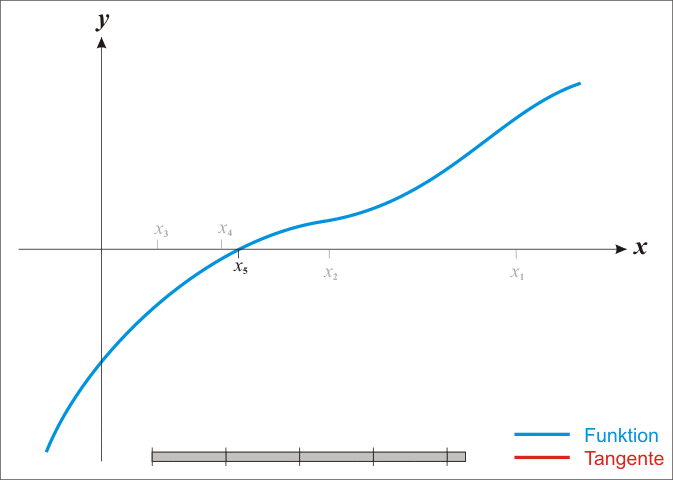
뉴턴법은 어떤 함수의 영점을 모를 때 아무점이나 찍은 후 그 점에서의 기울기를 구해서 점점 영점에 다가가는 방법이다.

우선 함수가 미분 가능해야하고 미분값이 0인 지점이 없어야한다. 효과적인 방법이긴 하나 여러 제약조건이 있다.

주로 공학용 계산기에서 방정식의 해를 구할 때 이 방법을 사용한다.

Gradient Descent

경사 하강법은 함수의 극소점을 찾기 위해서 기울기를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동하는 것을 반복하는 방법이다.

어떻게 보면 최적화하고자 하는 함수의 도함수의 영점을 찾는 것이라고 볼 수 있는데 뉴턴법과 다른 점은 뉴턴법은 상당히 급진적으로 이동하는 반면 경사 하강법은 이동할 거리는 조절하는 매개변수가 있고 (lr) 일반적으로 아주 낮은 숫자로 설정하여 천천히 이동한다.