Residual Learning

Degradation Problem을 해결하기 위해서 Residual Learning이라는 개념이 등장했습니다.

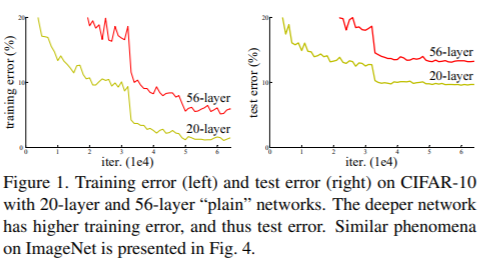
기존의 네트워크는 입력 x를 받고 여러 layer들을 거쳐 H(x)를 출력하는데 모델의 레이어를 더 깊게 쌓았더니 성능이 나빠졌다는 것은 다시 말해 차라리 레이어를 안 쌓는게 더 낫다는 것을 의미합니다.

그렇다면 성능이 나빠지는 시점(layer)부터 출력 H(x)가 입력 x가 되는 identity mapping을 하면 적어도 성능이 유지되지 않을까요?

그러면 좋겠지만 뉴럴 네트워크는 상당히 복잡한 형태의 비선형 함수여서 자기자신으로 돌아가는 방향으로 학습하는 것이 상당히 어렵습니다.

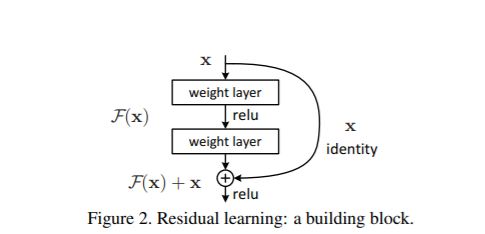
흔히 '잔차 학습'이라고 하는 Residual Learning은 H(x)가 아닌 출력과 입력의 차인 H(x)-x를 얻도록 목표를 수정함으로써 자기 자신으로 가는 identity mapping을 보장해줍니다.

Residual Learning을 통해 여차하면 자기 자신 그대로 매핑할 수 있으므로 층을 깊게 쌓아서 성능이 하락할 일은 없게 됩니다.

또한 identity mapping의 미분값은 1이고 이를 단순히 더함으로써 backward 시 gradient 소멸 문제를 해결할 수 있습니다.