Parametric Search완벽 이해하기(JAVA)

파라메트릭 서치를 얘기하기전에 이진탐색을 간단하게 살펴 보자.

이진탐색이란?

정렬된 데이터에서 원하는 특정값을 찾아내는 탐색 방법으로 시간복잡도는 logN을 가지는 효율적인 탐색방법이다.

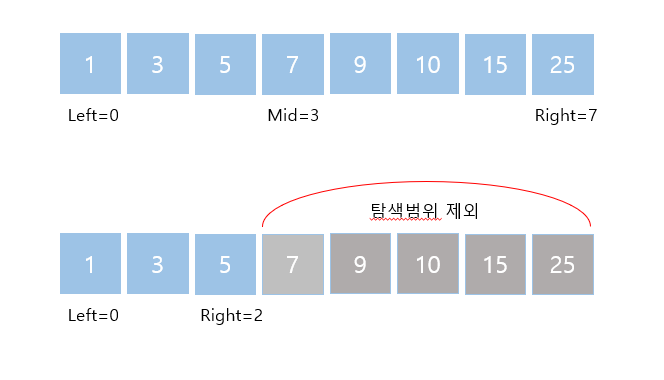
위 그림처럼 배열에서 3을 찾는다고 생각했을때
mid의 값인 7보다 작은값을 찾아야하므로 7보다같거나 큰 범위는 배제할 수 있다. 한번의 접근으로전체 배열 크기의 1/2부분을 제외 시킬 수 있는 효율적인 탐색 방법이라고 할 수 있다.

하지만 우리는 종종(꽤 자주) 중복된 값이 있는 배열이나 찾는 값이 없는 상황에 처할때가 있다. 이럴때 이 이진탐색원리를 응용한 Parametric Search를 사용해야한다.

Parametric Search에서는 조건에 따라 코드를 유동적으로 작성해야하는데 그 원리를 이해하게 되면 생각보다 쉽게 코드를 작성할 수 있다.

먼저 Parametric Search의 코드를 살펴보자

parametric search 코드

  public static int parametricSearch(int[] arr,int find) {
        int left=0;
        int right=arr.length-1;
        int mid;
        
        while(left<=right) {
            mid=(left+right)/2;
            if(arr[mid]>find) {//1️⃣부등호포함에 따라 중복 값중 어느방향 끝값인지 정해짐 
                right=mid-1;
            }else {
                left=mid+1;
            }
        }
       
        return right;2️⃣
    }
}

코드에서의 1️⃣과 2️⃣를 통해 경우를 구분할 수 있다.

1️⃣: mid값을 검증하여 해당하지 않는부분을 제외시키는 코드로 위 코드 기준으로는 mid위치의 값이 찾는 값보다 클때 mid포함 큰범위는 제외 되고 반대로 mid위치의 값이 같거나 작을때 mid포함 작은범위가 제외된다.
-> 찾고있는 값이 있을때 해당값이 있는범위도 제외되는 걸 알 수 있음

2️⃣: return을 left ,right를 하느냐에 따라 반환되는 값이 다른데, while문이(left<=right)일때 반복이 되고 left=right+1이 될때 while문이 종료되는 된다. 중복된 값이 없을때는 right에 찾는값보다 작은값의 인덱스가 들어가고 left에는 반대로 큰값의 인덱스가 들어가게 됨을 알 수 있다.

최종적으로 parametricSearch를 사용할때 네가지 경우로 나눌 수 있는데 1️⃣ 2️⃣를 통해 접근해보자.

1. 중복값의 가장 오른쪽이면서 만약 값이없다면 작은값
2. 중복값의 가장 오른쪽이면서 만약 값이없다면 큰값
3. 중복값의 가장 왼쪽이면서 만약 값이없다면 큰값
4. 중복값의 가장 왼쪽이면서 만약 값이없다면 작은값

1. 중복값의 가장 오른쪽이면서 만약 값이없다면 작은값 찾기

찾는 값이없을때 작은값을 찾기 위해서는 2️⃣을 통해 right를 return해야 하는 것을 알 수있다
중복된 값이 있다고 했을때 find값과 같거나 작은값을 만났을때 mid포함한 왼쪽범위를 제거 하면 최종적으로 mid는 찾는값의 오른쪽에서 멈추게되고 right=mid-1이 실행되므로 그대로 right를 return 하면 원하는 값을 찾을 수 있다.

 public static int parametricSearch(int[] arr,int find) {
        int left=0;
        int right=arr.length-1;
        int mid;
      
        while(left<=right) {
            mid=(left+right)/2;
            if(arr[mid]>find) {//1️⃣부등호포함에 따라 중복 값중 어느방향 끝값인지 정해짐 
                right=mid-1;
            }else {
                left=mid+1;
            }
        }
  
        return right;2️⃣
    }
}///1번 경우 코드

2. 중복값의 가장 오른쪽이면서 만약 값이없다면 큰값 찾기

이 부분은 위 문제와 다르게 answer변수를 두고 정답을 저장해야한다.(3️⃣추가해야함!)
찾는 값이없을때 큰값을 찾아내려면 2️⃣을 통해 left를 return해야 하는 것을 알 수있다.
중복값의 가장 오른쪽인 경우는 1️⃣을 통해 find값이 나왔을때 왼쪽을 제거 해야한다. 왼쪽을 제거하다보면 최종적으로 right에 중복값의 가장오른쪽의 인덱스 left에는 find값보다 큰값의 인덱스가 들어가게 된다.

1번과 다르게 경우에따라 다른 값을 return 해야하는 것을 알 수 있는데 -> answer변수를 두고 정답이있을시에는 answer를 없을때에는 left를 return하게 하면서 문제를 해결할 수 있다.

  public static int parametricSearch(int[] arr,int find) {
        int left=0;
        int right=arr.length-1;
        int mid;
        int answer=-1;
        
        while(left<=right) {
            mid=(left+right)/2;
            if(arr[mid]>find) {//1️⃣부등호포함에 따라 중복 값중 어느방향 끝값인지 정해짐 
                right=mid-1;
            }else {
                left=mid+1;
                if(arr[mid]==find)//3️⃣정답 저장 
                    answer=mid;
            }
        }
        if(answer!=-1)return answer;
        
        return left;2️⃣
    }
}///2번경우 코드

위 1,2번을 참고해서 3,4번 구현 가능합니다!!