A Programmable Neural-Network Inference Accelerator Based on Scalable In-Memory Computing

Problem to solve

1. 최근 연구들은 IMC를 programmable processor와 통합하였지만, IMC efficiency와 throughput을 달성하지 못함.
2. IMC는 compute energy efficinecy와 HW density/parallelism을 상당히 높여주지만, 큰 state-swapping overhead로 인해 architectural optimization이 따라주지 않으면 scalable execution이 힘듦.

How to solve

1. Workload-mappling technique을 통한 architectural design을 통해 hardware utilization을 극대화.
2. Architecture-software codesign.
   • PyTorch, TensorFlow 기반 library로 NN model을 chip에서 구동 가능하도록 quantize.
   • NN mapping toolchain으로 quantize된 NN을 architecture에 deploy.
3. Programmable array-of-cores IMC architecture로 여러 NN에 대해 mapping을 가능하게 함으로서 flexible parallelism을 지원하며, 이를 통해 최소한의 overhead로 scale-up이 가능.

IMC background

High-SNR IMC

IMC에서 가장 중요한 것은 연산이 robust 해야한다는 것인데, IMC의 본질적인 noise trade-off 때문에 달성하기 힘들다. IMC는 여러 row를 동시에 활성화하여 row-parallelism을 활용하지만, 이는 result의 dynamic range를 증가시켜 SNR을 감소시킨다.

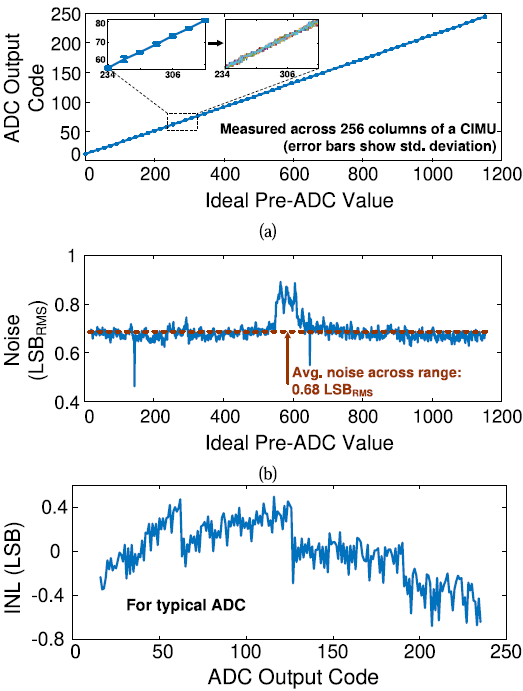
IMC는 아날로그 연산을 수행하므로 SNR이 중요한데, 최근에 등장한 high-SNR IMC는 캐퍼시터를 활용하여 1b multiplication을 수행한다. Lithography의 발전으로 캐퍼시터의 linearity와 temperature stability가 향상되어 수천개의 row에 대해 연산을 수행하여도 nonlinearity로 인해 dynamic range가 제한되지 않을 정도로 연산의 precision이 증가하였다.

Multi-Bit IMC

위의 1b IMC는 bit-parallel/bit-serial(BPBS)을 통해 multi-bit으로 확장되었다. BPBS scheme은 weight는 column 단위로 저장을 하고, input-vector는 row 단위로 sequential하게 입력된다. 연산 결과들은 column 단위로 ADC를 거치는데, 단순히 shift 연산을 거쳐 최종 연산 결과를 얻는다.

Challenges

IMC는 높은 efficiency와 throughput을 지니고 있지만, 높은 write cost와 hardware density로 scalable execution이 힘들다. Scalable execution을 위해서는 scheduling/mapping 등을 통해 hardware utilization을 최대화해야 하지만, 이는 weight update 등의 state-swapping overhead를 발생시킨다.

State-swapping overhead를 줄이기 위한 방법들은 여러가지가 제시되었다.

1. NN의 모든 weight를 IMC에 저장
   IMC는 저장과 연산을 동시에 수행하는데, 이 둘을 각각 다르게 최적화되어야 하므로 실현되기 힘들다. 또한, 이렇게 구현될 경우 utilization이 매우 낮다.
2. 연산별로 weight를 복사
   이 경우 utilization이 최대화 되지만, bit cell의 수가 너무 커져버린다.

Weight당 연산 횟수가 weight의 reuse 횟수의 최댓값을 결정하고, 이는 NN 모델과 batch size에 의해 결정된다. 본 논문에서는 latency-sensitive edge application에서 사용하는 batch size = 1을 가정하였다.

Rootline plot에 따르면, IMC의 energy efficiency를 높이려면 write overhead를 상쇄시키기 위해 operation/write가 높아야 한다. 8b data에 대해서는 operation/write가 150 이상은 되어야 최대 energy efficiency에 도달하였다.

IMC는 hardware density가 높아 high utilization을 위해서는 compute parallelism이 필요하여 flexible mapping이 필수적이다. Data-level parallelism과 더불어, layer간의 연산을 pipelining 하는 등의 operation-level paralleism도 가능하다. 그러나 이는 inter-stage buffering, latency 등의 overhead가 존재하므로 flexible optimization이 필수적이다.

Architecture

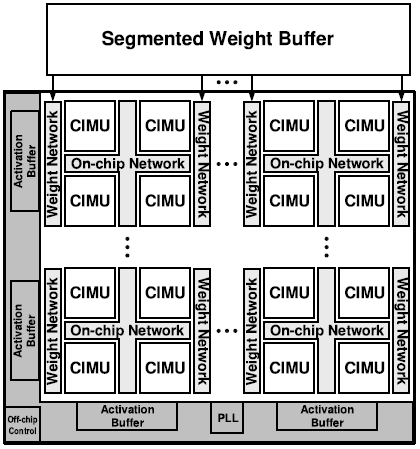
Scalable architecture는 여러개의 Compute-in-memory-units(CIMU)로 구성되어 있고, CIMU의 갯수는 area, throughput 등의 조건에 의해 조절 가능하다. 본 논문에서는 4x4 구조로 총 16개의 core로 구성하였다. CIMU는 weight-stationary 형식으로 연산을 수행하며, On-chip network(OCN)에 연결되어 입/출력 데이터를 주고 받는다.

Weight network는 weight buffer로 부터 weight를 CIMU에 전달하는 역할을 맡는다. Weight buffer는 28 MB 크기로, DRAM access를 최소화 하기 위해 크기가 설정되었다. 궁극적으로 weight network도 chip 내부에 집적되어야 하지만, 본 논문에서는 off-chip 형태로 구현되었다.

CIMU core

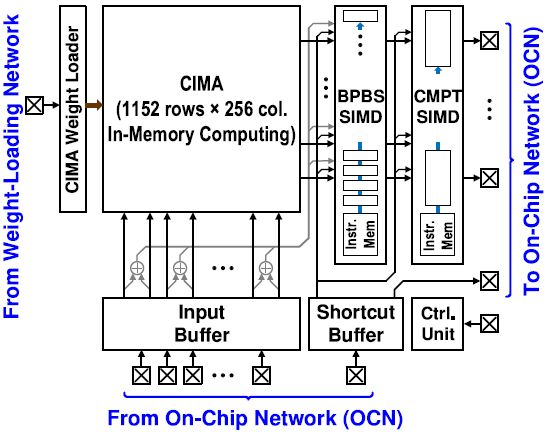
• Compute-in-memory array(CIMA)

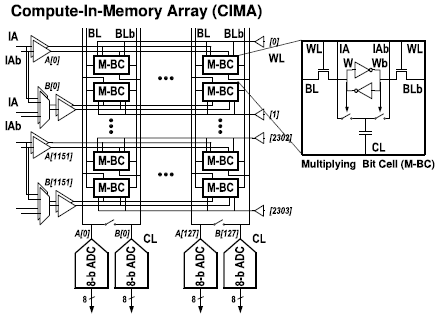
CIMA는 1152x256 크기의 캐퍼시터 기반의 IMC bit-cell이며, BPBS scheme으로 MVM(Matrix-Vector Multiplication)을 수행한다. Input-vector와 weight는 1~8 bit의 정확도를 가질 수 있다.

각 column의 CL(Compute Line)에는 8b SAR ADC가 연결되어있다. ADC resolution은 energy/area overhead와 quantization impact에 의해 결정된다. ADC는 CIMA의 약 20% area와 약 29%의 energy를 차지한다.

• Input buffer

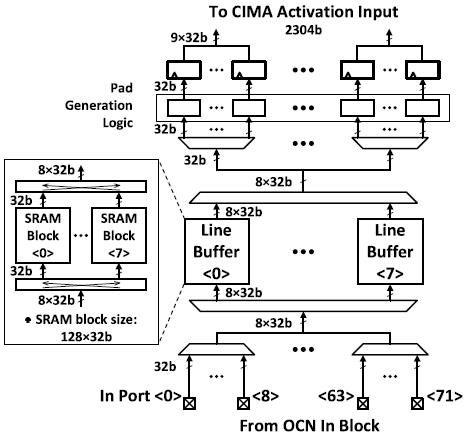
OCN으로 부터 input-activation data를 받아 CIMA에 전달한다. 여러 computation mapping, dataflow, reuse pattern에 따라 configuration이 가능하다. Input buffer는 8개의 SRAM-based line buffer들로 구성되어 있는데, line buffer 내부에 SRAM 앞/뒤로 switching network가 위치하여 in-buffer arrangement가 가능하다. 이를 통해 column gating을 활용해 energy efficiency와 SNR을 증가시킬 수 있다. 또한, local padding logic은 필요에 따라 zero padding을 생성한다.

• shortcut buffer

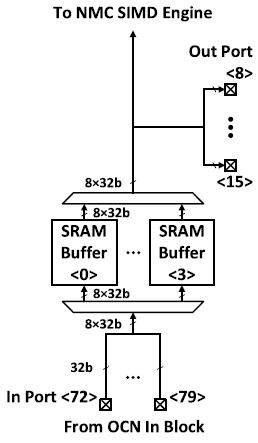
CIMA를 거치지 않고 SIMD engine으로 data를 바로 전달하거나, 곧바로 OCN으로 다시 전달할 수 있다. 이를 통해 residual connection, depth-wise shuffling과 같은 연산이 가능해 지는 등 flexible한 configuration이 가능하다. 또한, FIFO로의 사용도 가능해 layer-wise pipeline에서 latency를 맞추는데 사용할 수 있다.

• near-memory-computing(NMC) SIMD datapath
  CIMA로 부터 연산 결과를 받아 추가적인 digital operation을 수행한다.

  • BPBS SIMD

    

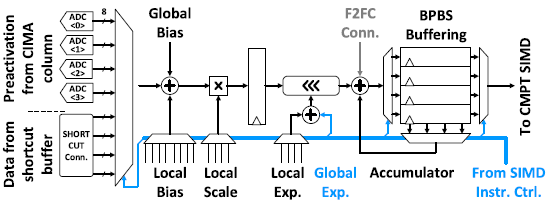
    Shifting/Addition에 특화되어 있으며, BPBS에서 output construction에 필요하다. Layout pitch와 CIMA의 throughput에 맞추기 위해 BPBS SIMD는 4개의 input을 multiplexing하여 연산한다.

    Adder/multiplier는 ADC gain/offset correction과 batch norm.에서 bias-shifting, scaling에 사용된다. Barrel-shifter는 2의 지승배의 곱셈과 BPBS output construction에 사용된다. Buffer와 accumulator는 CMPT SIMD에 data를 넘겨주거나 BPBS가 sequential한 동작을 하는데 사용된다.

    BPBS SIMD는 CIMA가 아닌 shortcut buffer로 부터 data를 받아 shortcut-path activation 연산을 수행할 수 있고, face-to-face-connection(F2FC)를 통해 인접한 CIMU에서 partial sum을 받아 accumulation을 수행할 수 있다.

  • Compute(CMPT) SIMD

    

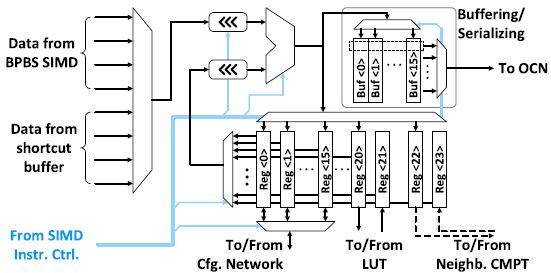
    Element-wise operation에 특화되어 있으며, activation function, scaling, biasing, pooling 등의 연산을 수행한다.

    CMPT SIMD는 BPBS SIMD와 유사하게 4개의 BPBS input과 4개의 shortcut buffer input 중에서 multiplexing하여 연산한다. BPBS SIMD로 부터의 입력을 다시 multiplexing함으로서 layout-pitch와 throughput matching을 할 수 있으며, SIMD datapath에서 bandwidth를 줄일 수 있다. 또한, CMPT SIMD의 input locality가 16 CIMA column이므로, LSTM 등에서 필요한 cross-element operation을 낮은 overhead로 가능하게 한다. Shortcut buffer로 부터의 input도 multiplexing함으로써 GRU 등에서 필요한 flexible한 activation path merging이 가능하다.

    ALU는 addition, subtration, multiplication 등의 연산을 수행하며, ReLU, average/max pooling 등의 연산도 수행한다. 연산 결과는 local register file에 저장되거나, output buffer로 향한다. Local register file은 연산 결과를 저장하는 16개의 general-purpose register, cross-element operation을 위해 인접한 CMPT SIMD와 data를 교환하기 위한 2개의 register, sigmoid나 tanh와 같은 nonlinearity에 사용되는 LUT를 위한 2개의 register로 구성되어 총 24개의 register를 가진다. Output buffer는 최종 연산 결과를 저장한 후 parallel bit stream 형태로 reshape하여 OCN으로 출력한다.

Programmable & Scalable NN Mapping

Layer mapping

1. Convolution layer

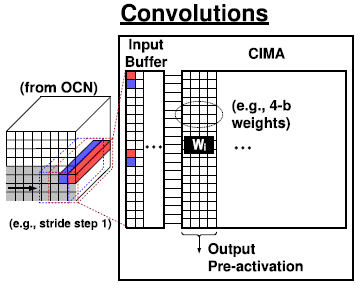
Kernel은 flatten되어 column-wise로 CIMA에 저장되고, input 또한 column-wise로 input buffer에 저장되어 있다가 CIMA에 입력된다. 여러 stride에 해당하는 input을 column-wise로 input buffer에 저장하여 여러 stride의 연산을 동시에 수행할 수 있다. Kernel이 CIMA의 바닥부터 저장되어, 사용하지 않는 row는 gating을 함으로써 energy efficiency와 SNR을 향상시킬 수 있다.

2. Shortcut/residual connection

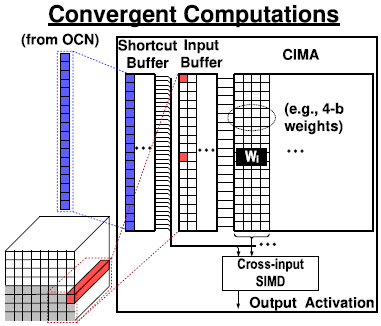
Input buffer는 OCN으로 부터 input을 받고, 동시에 shortcut buffer는 OCN으로 부터 shortcut input을 받는다. Input buffer는 input data를 CIMA로 전달하는데 반해, shortcut buffer는 input data를 NMC SIMD로 전달하여 merging computation을 수행한다.

3. Dense layer

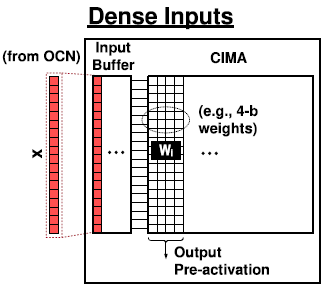
1x1 convolution과 같이 reuse data가 없는 dense한 input의 경우, input buffer는 OCN으로 부터 높은 bandwidth로 input을 받아 CIMA로 전달한다.

4. Recurrent/memory-augmented layer

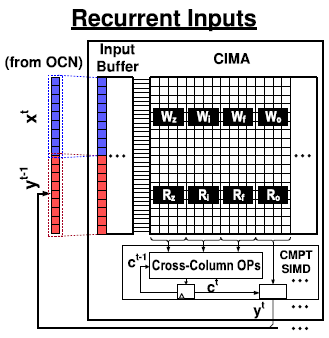
CIMU의 output이 OCN을 통해 다시 CIMU로 입력되는 형태이다. Input buffer는 새로운 input $x^t$와 hidden state $y^{t-1}$을 concatenate한다.

Layer scalability

1. Extension of output channels

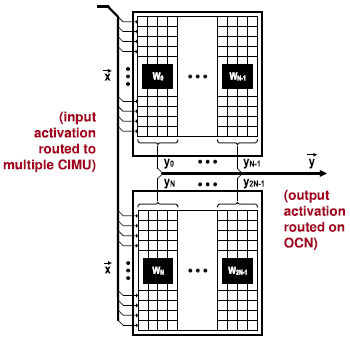
OCN이 input data를 여러 CIMU에 parallel하게 전달한다. 다수의 CIMU가 연산을 수행하고, 연산 결과는 다시 OCN에서 모아진다.

2. Extension of input channels

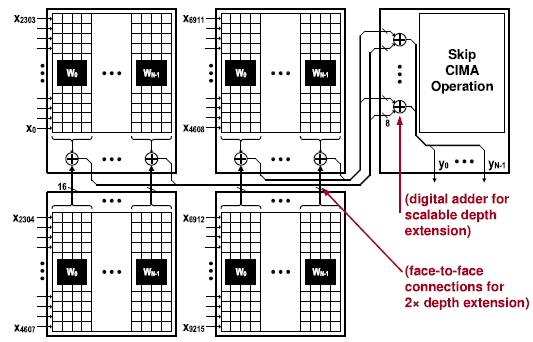
Compile 단계에서, kernel은 여러 CIMU로 mapping되도록 분할된다. Output을 계산하는 방법에는 2가지 방법이 있다.

• F2FC connection
  BPBS SIMD의 F2FC connection을 통해 인접한 CIMU로 부터 partial sum을 송/수신하여 최종 output을 계산한다. 이 방법은 추가적인 CIMU를 필요로 하지 않는다.
• Additional CIMU
  Arbitrary extention을 위해 CIMU의 output들이 추가적인 CIMU로 전달되어 input buffer에 뒤따라 오는 element-wise adder를 통해 최종 output을 계산한다. Output은 CIMA를 거치지 않으며 곧장 OCN으로 전달되거나 NMC SIMD에서 추가적인 연산이 수행될 수 있다.

Analysis of mappings exploiting flexible parallelism

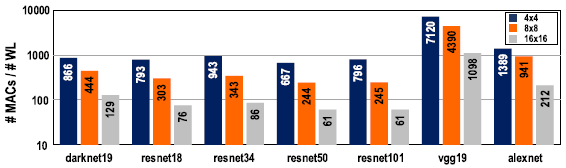
CIMU의 갯수를 4x4, 8x8, 16x16으로 설정하여 #MAC/#write를 비교하였을 때, CIMU의 갯수가 증가함에 따라 operation/write가 감소하였다. 8b data의 경우 최대 energy efficiency를 달성하기 위해서는 operation/write가 150 이상이 되어야했는데, 16x16 CIMU의 경우 이 수치보다 낮아져 high parallelism을 위한 추가적인 접근이 필요하다.

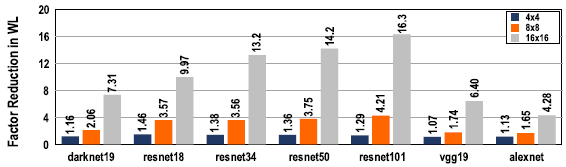
Data-level parallelism(replication)과 operation-level parallelism(pipelining)을 포함한 flexible parallelism을 위한 architectural support는 state-loading overhead를 최소화하며 hardware utilization을 증가시키는 등, scalable execution을 위한 compiler optimization을 가능하게 한다. 단순히 replication을 하는 대신, data/operation parallelism을 동시에 활용함으로써 scale을 키움에 따라 write operation의 증가율을 감소시킬 수 있었다.

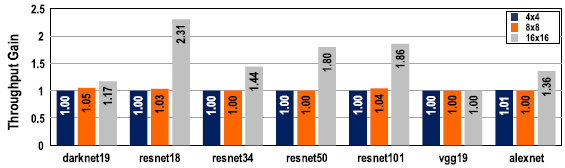
논문에서 주장한 optimization을 통해, 대부분의 경우 throughput이 증가하였고 operation-level parallelism에 크지 않은 overhead가 존재하였다. 그러나, 몇몇의 경우 data-level parallelism이 최선의 선택이었다. 이는 throughput이 operation/write와 강한 상관관계를 가지며, optimization을 통해 scale이 커짐이 따라 write의 증가율이 감소하여 operation/write가 증가하였기 때문이라고 생각된다.

Measurement results

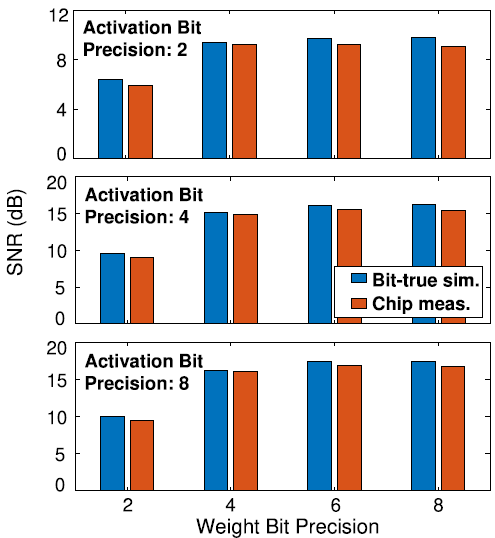
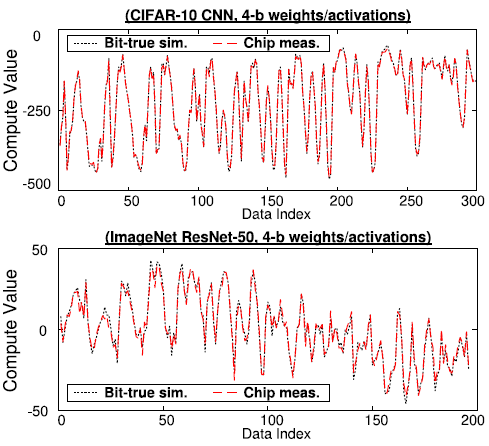
여러 precision의 Weight와 activation에 대해 SNR을 측정하였을 때, 실측한 SNR은 floating-point를 integer로 변환할 때와 ADC에 의한 quantization을 simulation했을 때의 SNR과 유사한 값을 보여주었다. 이는 quantization이 IMC 연산의 주요한 noise source임을 나타낸다. Quantization은 digital적으로 모델링이 가능하므로 연산에 대한 robust abstraction이 가능하다.

Software

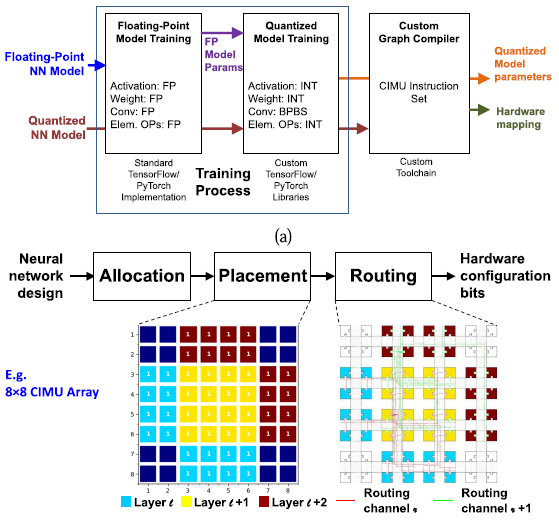
본 논문의 architecture는 software mapping algorithm/tool과 co-design되었다. Mapping을 위한 과정은 다음과 같다.

1. Floating-point parameter로 NN 학습
2. BPBS와 SIMD engine의 quantization effect을 고려하여 모델을 quantize
3. Graph compiler와 mappling tool을 통해 mapping
   3-1. Graph compiler가 hardware execution을 최대화하도록 allocation/scheduling 수행
   3-2. Simulated-annealing-based algorithm에 따라 CIMU 간의 통신이 최소화되도록 physical placement 수행
   3-3. Heuristic optimization algorithm에 따라 OCN routing 수행