Paper Link

https://aps.arxiv.org/pdf/2309.11054.pdf

Introduction

• 최근 LLM을 이용하여 수학 문제를 푸는 task가 굉장히 활발히 연구 되고 있음
  • 수학 문제를 해결하는 것은 LLM에서 multi-step의 추론을 하는 가장 이상적인 task이기 때문
  • 특히, 최근 LLM의 등장에 의해 단순한 NLP Task는 모두 해결되는 추세이나 용인될 수 있는 CoT를 생성하는 등의 복잡한 task에 대해서는 아직까지는 미제
  • 과연 LLM에 어떻게 Prompting을 주거나 shot learning을 주어야지 잘 처리할 수 있을지에 대해 찾는 것이 최근 연구이고, Math Problem에서는 program식으로 CoT를 주는 방법이 연구되고 있음
• 해당 논문에서는 여러 CoT의 기법들(Nature Language, Self-Describing program, Comment-describing, non-decsribing)과 여러 언어(Python, Wolframalpha)를 이용하여 직접 성능을 비교하는 작업을 수행함
• Program CoT 같은 경우 실행이 굉장히 쉬우므로 그게 실제로 돌아가는지(실행률)을 측정하기 굉장히 쉽다는 장점이 있음
• 3개의 Dataset($\texttt{GSM8K}$, $\texttt{MathQA}$, $\texttt{SVAMP}$)에 대해 검증하였을 때,
  1. Program CoT가 일반적으로 NL로 전개한 CoT보다 더 좋은 성능을 보임.
  2. SDP와 CDP는 NDP에 비해 월등히 높은 성능을 보였으며, SDP가 일반적으로 CDP보다 성능이 좋았음
  3. WolframAlpha보다는 Python으로 Program을 구현하였을 때 성능이 더 좋았음
  4. 각 유형의 CoT마다 장점이 있으며, 이들을 결합하여 더 좋은 CoT 기법을 만들어 낼 수 있을 것으로 사료됨.

CoT Design

Sample

Natrual Language CoT (NL)

• 말 그대로 자연어로, 말을 풀어서 CoT를 생성하는 방법
• "Let's think Step By Step"을 사용하면 조금 더 성능이 좋아진다는 분석이 있었음

Self-Describing program

• 변수명을 문제의 설명 부분으로 설정하는 방법
• 예를 들어 위의 sample이 있다면 변수명들은 a_is_two_years_older_than_b, b_is_twice_as_old_as_c와 같이 문제의 부분을 그대로 긁어서 변수명으로 설정하는 방법
• 변수명에 설명이 다 들어가있기 때문에 multi-step이나 step-by-step 추론을 할 때 변수명을 활용함
• 문제의 부분을 그대로 긁어서 변수명을 생성하기 때문에 변수명 규칙만 지키고 코드만 잘 생성하면 바로 실행하여 답을 추론할 수 있다는 장점이 있음
• 변수명을 만들어내기 위해서 일련의 규칙을 정해놓음
  1. 프로그램이 무엇을 의미하는지 직관적으로 파악하기 위하여 고수준의 operation만을 사용함
  2. 문제의 순서대로 변수명을 설정하였음
  3. 변수명을 의미있고 밑줄이나 소문자 등을 이용하여 몇몇 국룰(?) convention을 이용하여 build하였음

Comment-Describing program

• 위의 SDP 같은 경우 문제가 길어질수록 일관된 설명이 아닐 수도 있음.
  • 앞에서는 A로 설명이 되었다가, 뒤에서는 갑자기 B로 바뀌어서 설명이 되거나 하면 다시 설정을 하는 Error가 발생
• 또한, 문장 내에서 충분한 단서를 주지 않을 경우도 있음.
  • 현재 sample 문제 같은 경우 직관적으로 $a+2=b=2c$, $a+b+c=27$로 주었지만 이렇지 않은 경우도 종종 있음
  • 이러한 경우 변수명에서 충분한 정보를 가져오지 않는 경우가 많음
• 그렇기 때문에 변수명은 단순히 설정을 하고, 주석으로 문제의 설명을 작성하여 이를 reasoning에 사용

Data Collection

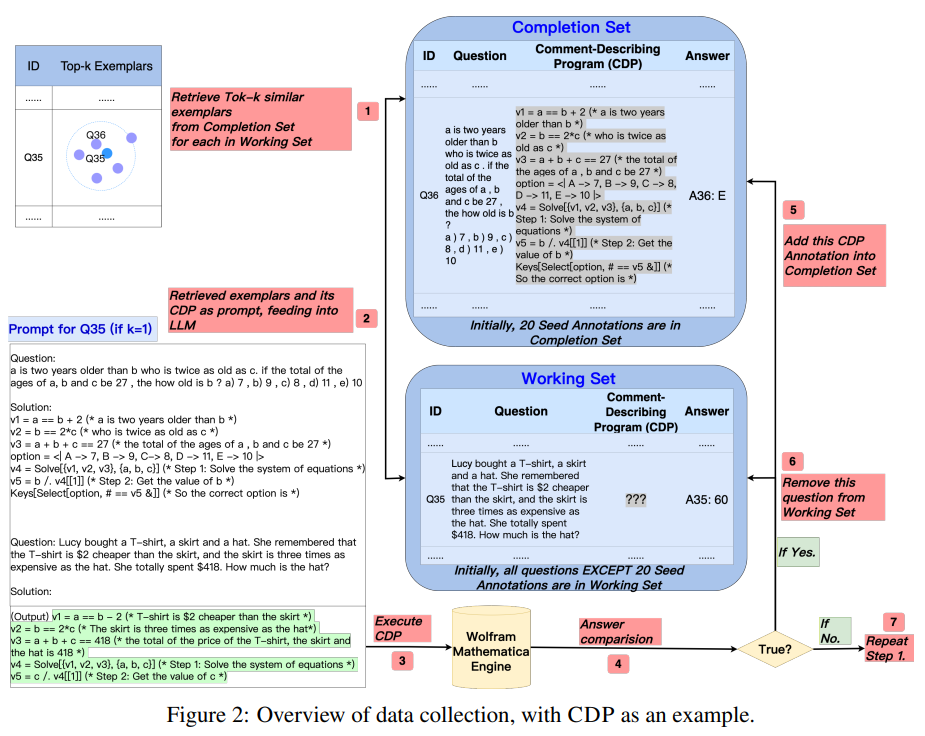
• 이전에 설명했던 $\mathtt{GSM8K}$, $\mathtt{MathQA}$, $\mathtt{SVAMP}$ dataset을 이용하여 구성할 예정
• 위 Training set에 있는 것들을 LLM을 이용하여 자동으로 생성할 것이며, Few-Shot Learning을 이용
• Few-short learning을 위해 일부 데이터들은 직접 수집하여 만들 것이고, Few shot으로 LLM을 이용하여 annotation을 진행
• 자세한 과정은 다음과 같음
  1. 먼저 데이터셋에서 SDP에서 $20$개, CDP에서 $20$개를 무작위로 추첨하여 직접 손으로 annotation을 실행, 이를 모두 completion set에 집어넣고, 나머지 data들은 모두 working set에 집어넣음
  2. 모든 질문들을 OpenAI사의 $\texttt{text-embedding-ada-002}$를 이용하여 embedding 진행
  3. working set에 있는 질문들에 대해 completion set에 있는 것들 중 $K$개의 비슷한 예제를 뽑고, LLM에 $K$개의 Prompt를 모두 few-shot learning으로 집어넣음. 이때, CDP면 CDP의 completion set에, SDP면 SDP의 completion set에 집어넣고, 유사도를 따지는 과정은 $2$번에서의 embedding 결과의 cosine similarity를 이용
  4. $3$번에서 얻은 CDP / SDP를 실제로 wolfram alpha나 python을 이용하여 연산하였을 때의 결과와 ground-truth와 실제로 비교
     이때, 데이터셋에 따라 답이 numeric할 수도, multiple-choice도 있을 수 있으므로 이에 대한 보정도 추가적으로 실시
     이렇게 해서 만들어진 set들은 다시 Completion set에 들어가게 됨
  5. 위의 $3$번과 $4$번 과정을 working set이 없거나 더 이상 completion set에 추가되지 못할 때 까지 반복 (대략 $3$번 내지 $5$번 정도 실행)
  6. 마지막으로 working set에 있는 sample들에 대해서는 직접 수작업을 통하여 annotation을 하고, 이후 이를 completion set에 넣음으로써 최종적으로 완료

Methodology

• 총 3개의 방법을 사용하고, 기본적으로 SFT(Supervised Finte-Tuning)을 사용하고 이후 Majority Voting(Self-consistency decoding)과 Reward model을 활용한 Reranking 기법을 선택적으로 적용

SFT(Supervised Fine-Tuning)

• 위에서 얻은 Dataset을 사전훈련된 언어모델(해당 paper에서는 Galactica를 활용)에 Fine Tuning을 진행
• 해당 Fine tuning의 목적은 주어진 질문에 대한 정답을 이끌어내는 것을 최대하기 위함
• Evaluation stage에서는 최종 정답만을 이용하여 정답률을 따지며, 정답을 내는 과정 같은 경우 Program CoT는 Program을 실제로 돌려서 답을 추출

Majority Voting

• 위의 SFT로부터 훈련된 모델에 question을 모두 넣어, 몇개의 확률 높은 prompt를 모두 뽑아냄
• 이후 그 sample들에 대해 가장 정답이 높아보이는 voting을 실시, 여기에서 나온 답을 최종답으로 결정
• Temperature sampling strategy를 사용하고, 해당 기법은 sampling 전략이나 temperature parameter에 딱히 크게 변동이 없기 때문에 $T=1.0$으로 set하여 시행한다.

Reranking with Reward Model

• 단순히 SFT하여 나온 최종 답을 사용하는 것이 아니라, majority voting처럼 몇몇개의 답을 뽑아낸 후 그중 "가장 옳다"라고 판단되는 답을 다시 Classifier을 이용하여 추출
• 이때 correct / incorrect에 대한 판단을 하기 위해서는 정답이 필요한데, 이는 SFT 과정에서 $2nd$ checkpoint에서 모델을 가져와서 sampling을 진행 $\Rightarrow$ 이렇게 하는 이유는 정답에 대한 diversity를 늘리기 위함
• 이를 바탕으로 Reward Model(Classifier)를 학습하여, 기존에 SFT만의 모델만 사용하는 것이 아니라 여기에서 추가적으로 Reward Model을 통과시켜서 최종 답을 추출

Experiment

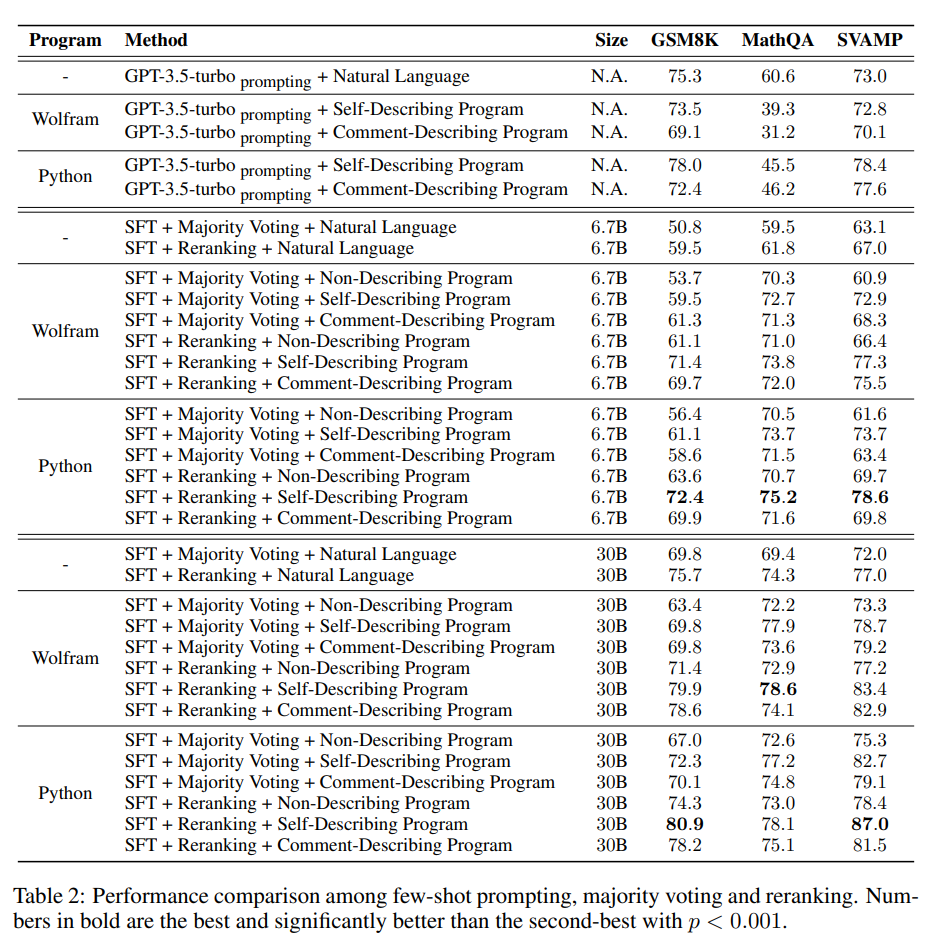
Analysis

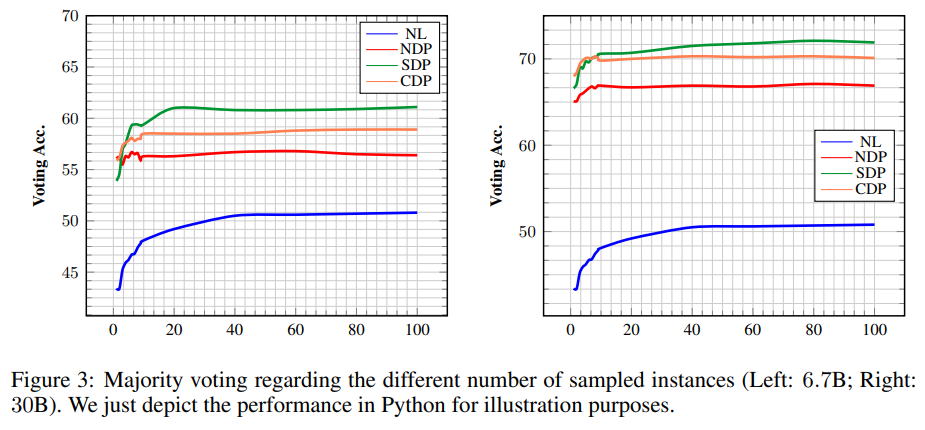
Number of Instances for Sampling

• Majority Voting 같은 경우 $K$개의 후보를 sampling하여 여기에서 Voting을 진행하게 됨
• 이때 $K$를 $1$에서 $100$까지 변화시키게 되었을 때, NL이랑 SDP 같은 경우 $K$가 $30$일 때부터 stable해지게 되고, 그 이외의 것들 같은 경우 모두 $30$보다 작은 범위에서 안정적으로 변하였음
• 이외에도 NL보다 나머지 NDP, SDP, CDP가 훨씬 높았으며 SDP와 CDP 중에서는 SDP가 더 좋은 성능을 보임

Representation sampling statistics

• 문법적으로 올바른지(실제로 실행이 되는 비율) / 정확한 답을 내는지(precision) / $100$개의 sampling한 결과 중 적어도 하나의 정확한 정답이 있는지에 대한 여부 ($\text{correct}@100$)에 대한 결과를 report한 표임

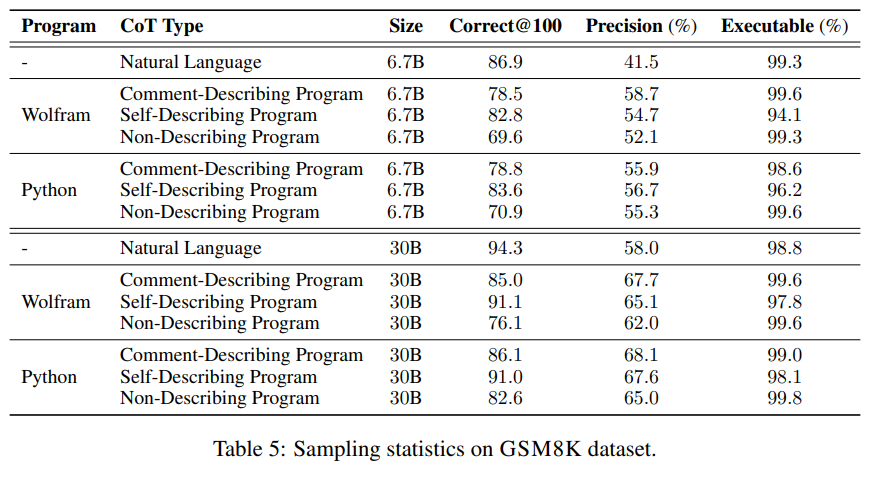
• NL 같은 경우 $6.7\rm B$, $30\rm B$ 대부분이 실행가능하고($99.3\%$)모두 correct 같은 경우 굉장히 높으나, 즉 제대로 실행은 되나 그에 대한 top result의 정답률은 좋지 않음을 알 수 있음
• 즉, 실행이 가능하게는 뽑지만 말로 풀어쓴 글들 같은 경우 Chain of Thought가 쉽지 않음을 알 수 있음
• 반면, Program CoT 같은 경우 $6.7\rm B$ 같은 경우엔 SDP와 같이 변수명에 error가 생길 수 있는 것들은 Executable 수치가 조금 낮음을 알 수 있음
• 다만, 정확률과 $\text{Correct}@100$은 모두 SDP가 월등히 높았으며, $30\rm B$ 같은 경우 $97.8\%$로 어느 정도 높은 실행률을 뽑아냄을 알 수 있음
• 이는 CDP 같은 경우엔 일단 실행이 가능하게 하고, 그것이 엄청 높은 정확률을 의미해주진 않지만 어느 정도 인정할 수 있는 output을 낸다면 SDP는 실행이 불가능한 것들도 두지만 이미 가능한 것들에 대해서는 높은 퀄리티로 뽑아냄을 알 수 있음

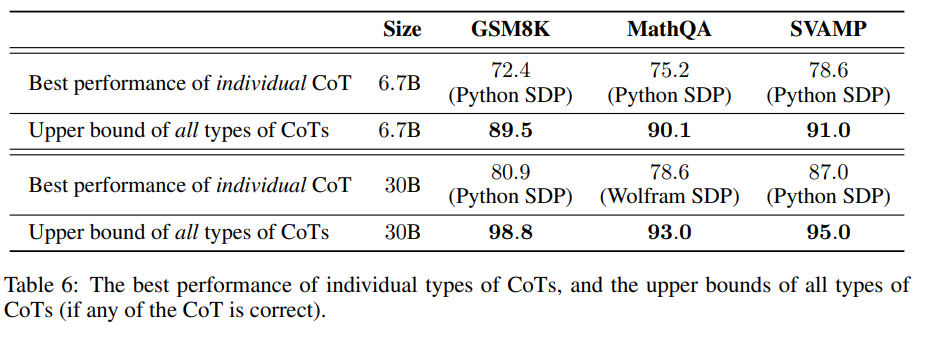
Upper Bound

• 모든 CoT를 포함하여 낼 수 있는 최대 상한선의 결과를 냈을 때를 비교하는 task를 수행 $\Rightarrow$ 이를 통해 각 CoT의 잠재력을 판단

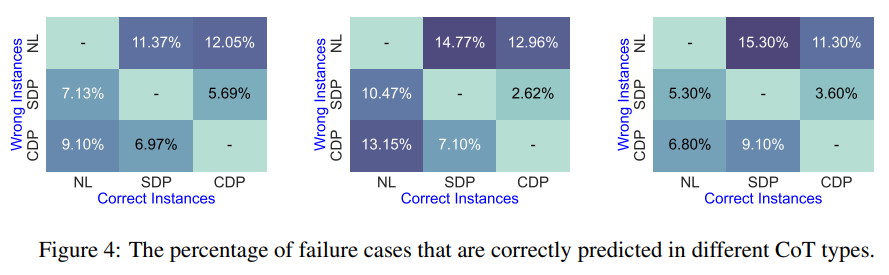
• 위의 Figure $4$는 각 CoT가 틀린것들 중 다른 CoT는 맞은 비율을 따진 것이며, $3$개는 각 Dataset에 대해 표시한 것이다.
• 위에서 관찰한 바로 SDP 같은 경우 Executable한 결과를 많이 내지 못하는데, NL에서 $5\%\sim10\%$ 정도 보완해줌을 알 수 있음
• 이는 각각을 융합하여 적절하게 사용하는 것이 좋다라는 것을 의미하는 바

Conclusion

Limitation & Future work (My opinion)

Opinion about SDP

• 다만, 해당 논문에서 High-level operation이 무엇인지에 대해 제대로 밝히지 않았기 때문에 이 연산들이 무엇인지에 대해서는 코드를 통해 확인을 해봐야 할 듯 함
• 추가로, 문제의 순서에 맞게 변수명을 설정하였다고 하였는데, 수학 문제 같은 경우 nested에 nested가 되는 재귀적으로 문제가 설명되는 경우가 많음. 이러한 경우, 변수명이 제대로 설정이 되었을지에 대한 추가적인 claim이 필요함
• 또한, 문제 중간에 변수가 새로새로 설정이 되는 경우가 많음. 이런 경우, 과연 변수가 새로 들어오는 환경에서는 변수명을 어찌 설정을 할 것인가에 대한 설명도 필요할 듯 함

Opinion about CDP

• 위의 SDP에 비해 조금 유동적이다라는 느낌은 받았지만, 설정하는 과정에서 SDP와 CDP의 다른 점에 대해 크게 인지를 하지는 못하겠음.
• 주석으로 다나, 이걸 변수명으로 설정하나 크게 다를 것은 없을 것으로 생각. 다만, 변수명 설정 과정에서 information loss가 발생한다면 이는 꽤 유의미할 것으로 생각

Limitation

• 해당 모델은 pretrained model로 code가 같이 학습된 모델을 활용함
  $\Rightarrow$ 즉, 최근의 chatgpt나 Bard처럼 chatting형에서 더 나아가서 code에 대해 학습시킨 Pretrained된 모델이 필요함
  $\Rightarrow$ 이 때문에 최근의 좋은 모델들이 나와도 활용할 수 없다는 단점이 있음

Improvements (Future Work)

• 분명히 문제를 설정하는 과정에서는 SDP가 더 좋은 것으로 보임. 실제로 성능도 SDP가 CDP보다 더 좋은 성능을 보임
• 하지만, 중간에 계산이 들어가는 과정에서는 CDP가 조금 더 유동적으로 대처할 수 있다는 장점이 있음
• 변수명에 cdp_나 sdp_와 같은 특수 문자들을 넣어줌으로써 이를 구분하고, 주석을 필요에 따라 달아주면 더 좋은 성능을 낼 수 있지 않을까?라는 생각이 듦
• 또한 앞에서 말했다시피 High-lvel operation만 적용했는데, 단순 산술작업 외에도 기하적인 문제를 같이 prompting으로 풀 수는 없을까에 대한 생각도 필요함
• 기하적인 문제 외에도 최근 graph를 통하여 분석할 수 없을지, 만약 graph를 그릴 수 있다면 graph와 annotation된 question을 multimodal로 input을 준다면 해석적인 문제를 더 잘 풀 수 있을지에 대한 부분도 고려해볼 수 있음