BOJ1002-터렛 (python3)

간만에 예전에 풀다가 틀려서 포기했던 문제를 가져와서 다시 풀어보았다.

문제 속에서 공식을 찾으려고 하다보면
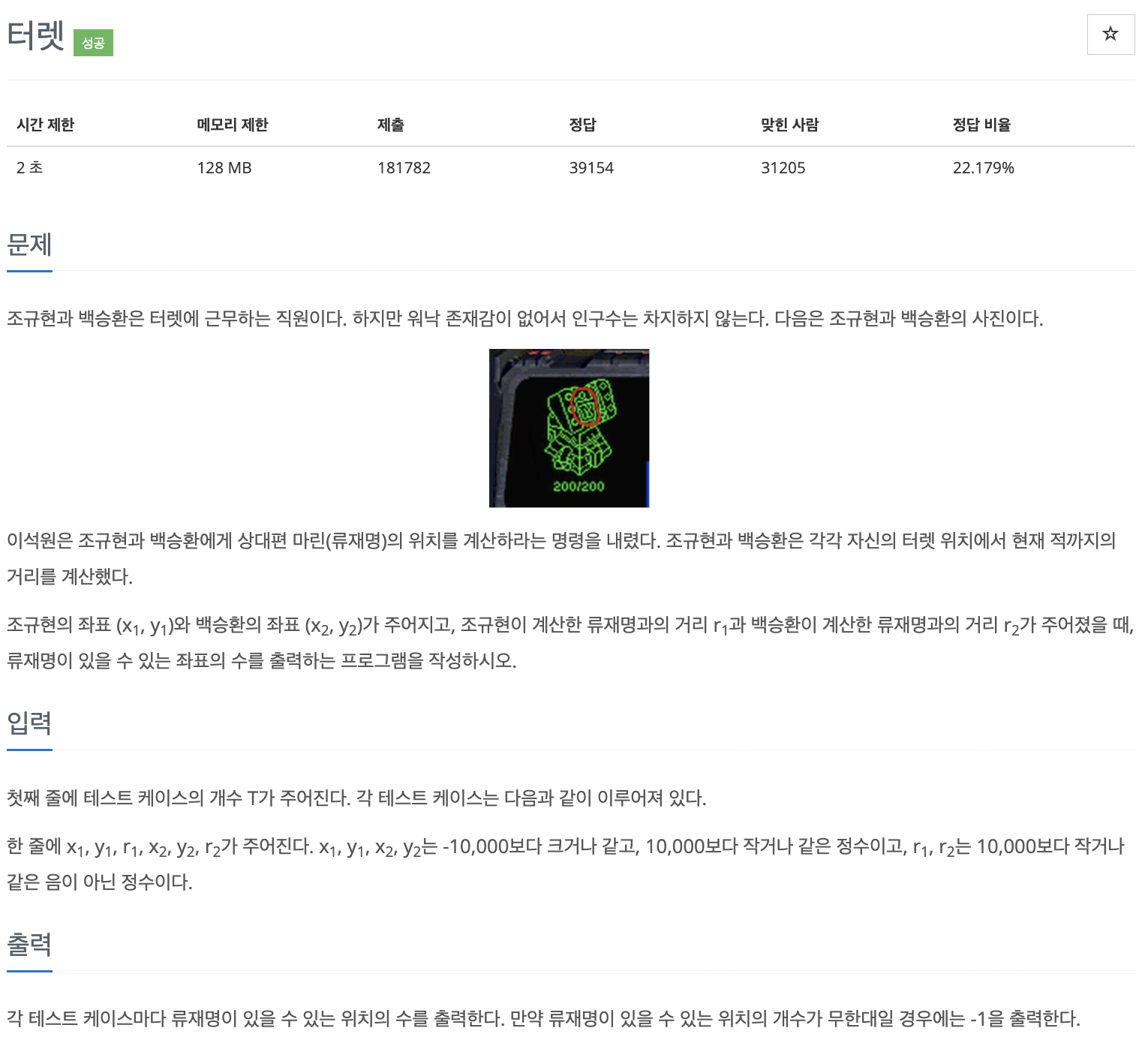
두 점 사이의 거리를 구하는 공식을 통해
두 원의 접점의 개수를 구하면 되는 방식이라는 것을 알 수 있다.

두 원이 배치되는 유형은 크게 6가지의 경우로 나눌 수 있다.
1. 원이 완전히 겹치지는 않지만 겹쳐 두점이 만남 -> 접점 2개
2. 원이 완전히 겹침 -> 접점 무한(-1)
3. 원이 외접 -> 접점 1개
4. 원이 내접 -> 접점 1개
5. 한 원이 다른 원을 포함하지 않고 접하지도 않음 -> 접점 0개
6. 한 원이 다른 원을 포함하고 접하지 않음 -> 접점 0개

이 경우에 따라 두 점 사이의 거리 D와 반지름 길이의 차를 공식화하여 계산하면 문제를 풀 수 있다.

나의 경우,
list로 숫자를 받았기 때문에 따로 이름붙이지 않고 인덱스로 계산하여 다소 가독성이 떨어지지만, 변수에 이름을 붙여 입력을 받아 가독성을 높일 수 있다.

아흑 몇트만에 성공한건지..

결국 11트만에 성공..

import sys
import math
n = int(sys.stdin.readline().rstrip('\n'))
case_list = list(list(map(int,sys.stdin.readline().rstrip('\n').split()))for _ in range(n))
for i in case_list:
    D = math.sqrt((i[3]-i[0])**2+(i[4]-i[1])**2)
    if D==0 and i[2]==i[5]:
        print(-1)
    elif D<i[2]+i[5] and D>abs(i[2]-i[5]):print(2)
    elif D==i[2]+i[5] or D==abs(i[5]-i[2]):print(1)
    else: print(0)