출처 : 파이썬 알고리즘 인터뷰

정렬을 깨부수겠다고 마음먹은지 이주가 지났다. 그동안 푼 문제라곤...sortlist와 merge intervals 두 문제 뿐...그러나 지금이라도 정신차리기~

오늘의 문제 1

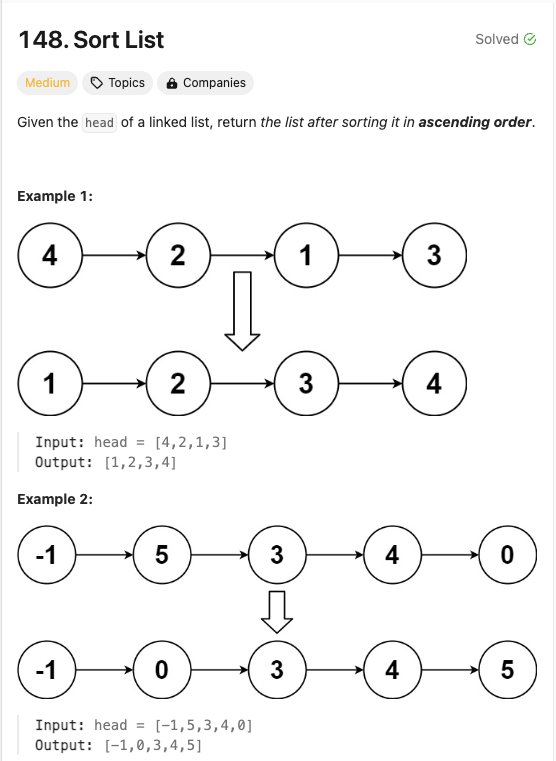
연결리스트로 입력받아 정렬한 후 연결리스트로 반환하는 문제이다.

이 문제의 키 포인트는 입력도 반환값도 연결리스트여야 한다는 것이다.

생각의 흐름

연결리스트는 전체 길이를 알 수 없다.

-> 분할정복에 이용하기 위해 길이를 파악할 수 있어야 함

-> 런너기법 을 사용해서 반으로 계속 나누고

-> 나눈 연결리스트를 정렬하면서 연결하기

접근 1

런너기법

연결리스트 같이 알 수 없는 길이를 가늠할 때 사용하는 것으로,

half, slow, fast 세 포인터가 있으며, slow는 한칸씩, fast는 두칸씩 이동한다.

fast가 연결리스트의 끝에 도달했을 때 slow는 자연스럽게 연결리스트의 중간에 도달할 수 밖에 없다!

(이동단위가 정확히 두배 차이 나니까)

slow를 기준으로 분할한다는 개념!(half는 slow의 바로 전단계를 가리키도록 한다.)

half, slow, fast = None, head, head # 초기화
whlie fast and fast.next:
  half, slow, fast = slow, slow.next, fast.next.next
half.next = None # half 다음에 연결을 끊으면서 연결리스트 분할

접근 2

정렬하면서 붙이는 함수가 필요하다.

개념 : 분할된 두개의 연결 리스트가 모두 존재하는 경우, 두 리스트의 각 head가 가리키는 값을 제대로 정렬하고, (그 다음을 가리키는 것과 남은 리스트들)을 다시 정렬머지해준다는 논리

def mergeTwoLists(self, l1, l2):
  if l1 and l2:
    if l1.val > l2.val:
      l1, l2 = l2, l1
    l1.next = self.mergeTwoLists(l1.next, l2)
    
  return l1 or l2

1번 문제 최종 코드

def mergeTwoLists(self, l1, l2):
  if l1 and l2:
    if l1.val > l2.val:
      l1, l2 = l2, l1
    l1.next = self.mergeTwoLists(l1.next, l2)
    
  return l1 or l2

def sortList(self, head):
  if not (head and head.next): return head

	half, slow, fast = None, head, head
  while fast and fast.next:
    half, slow, fast = slow, slow.next, fast.next.next
  half.next = None
  
  l1 = self.sortList(head)
  l2 = self.sortList(slow)
  
  return self.mergeTwoLists(l1, l2)

오늘의 문제 2

입력 받은 리스트 간의 구간이 겹치는 곳이 있으면 합쳐서 반환하는 문제이다.

생각의 흐름

겹친다? = 다음의 시작 지점이 전 지점의 끝 지점보다 전에 있는 경우

-> 항상 성립하기 위해서는 시작 지점이 정렬된 상태여야 함

필요한 것 : 정렬된 이중 리스트, 겹치는지 확인해주는 if문

접근 1

이중리스트를 정렬하는 방법 익히기

sorted(intervals, key=lambda x: x[0])

위와 같은 방식으로 정렬하면, x[0]을 기준으로 정렬한다.(첫번째 요소)

다음과 같이 사용할 것이다.

for start, end in sorted(intervals, key=lambda x:x[0]):
	(...)

접근 2

겹치는 구간을 검색

-> 현재 탐색하고 있는 구간의 시작과 바로 전 구간의 끝이 겹치는지를 확인

-> 겹치는 경우 : 종료 지점 갱신(기존의 것이 더 클 수 있으므로 max함수 사용)

if merged and start(현재구간) < merged[-1][1]:
  merged[-1][1] = max(merged[-1][1], end)
else:
  merged += [start, end]

2번 문제 최종 코드 O(n log n)

def mergeIntervals(self, intervals):
  merged = []
  for start, end in sorted(intervals, key=lambda x:x[0]):
  	if merged and start < merged[-1][1]:
      merged[-1][1] = max(merged[-1][1], end)
    else:
      merged += [start, end]
  return merged