BFS(Breadth-First Search) 알고리즘이 최단 경로를 보장하는 이유 - 게임 맵 최단거리

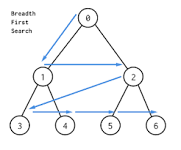
일단 BFS 알고리즘에 대해서 간단히 설명하자면 너비 우선 탐색으로도 불리며 노드 뎁스를 끝까지 갔다가 다시 돌아와서 탐색하는게 아니라 아래 이미지처럼 자기 레벨의 뎁스들 부터 먼저 탐색하고 그 다음 뎁스로 넘어가서 탐색합니다. 보통 BFS는 큐를 사용하고 DFS는 스택 또는 재귀함수로 구현됩니다.

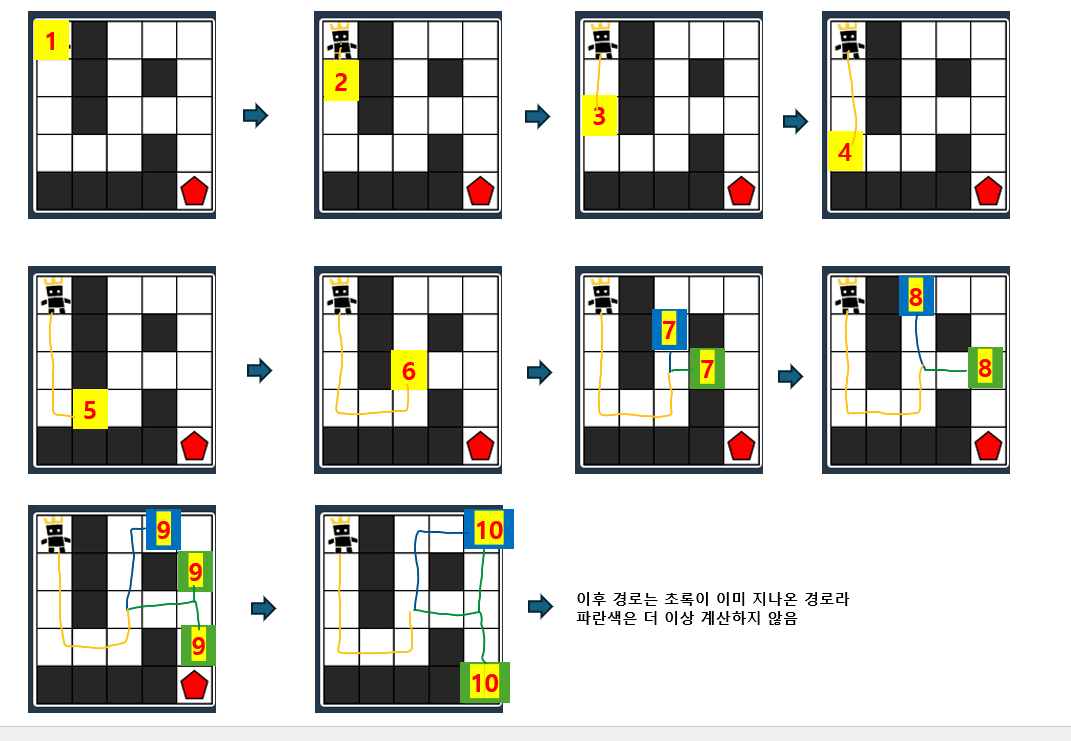
회사 다닐 때 여유가 없어 잘 하지 못했던 알고리즘을 공부중에 BFS와 DFS를 오랜만에 보게 되어 프로그래머스에서 문제를 하나 풀게되었습니다.

분명 신입시절 공부했던거고 문제에 BFS를 이용해서 구하라고 적혀있는데도 불구하고 큐를 떠올리지 못했고ㅠ 그렇게 몇 번 실패 후에 결국 치팅을 해버렸습니다.. (전체 소스는 게시글 최하단에 있습니다.)

치팅을 할지언정 분석은 확실히하자는 마음으로 소스를 보던 중 '근데 최단거리를 찾는데 왜 좋은거야?'라는 의문이 생겼습니다. 이게 직관적으로 이해가 되지 않아서 직접 메모장으로 큐를 담아가며 PPT로 그림을 그려봤습니다.

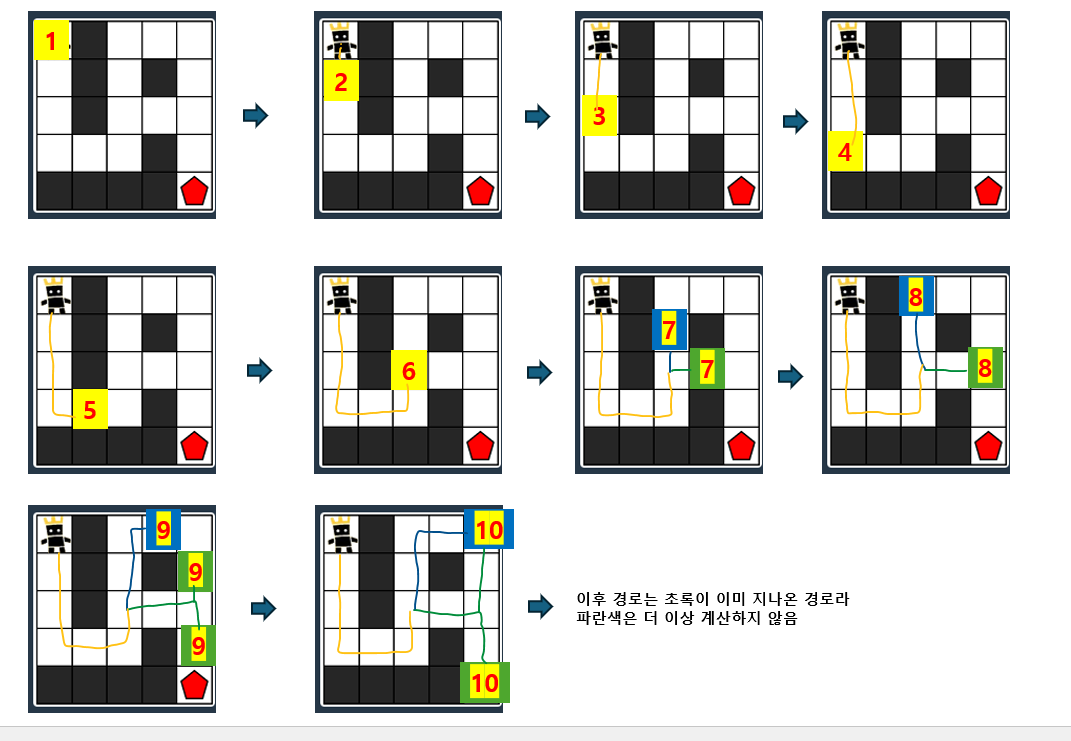
그리다가 깨달은 것은 일단 DFS처럼 재귀함수를 돌렸다면 파랭이가 초록이보다 먼저 끝까지 갔겠구나 싶었고 큐를 이용한 너비 우선 탐색, 이미 방문했던 곳은 계산하지 않는다 는 두 가지 특성이 있어서 최단경로를 찾는게 가능하구나를 깨달았습니다. 모든 격자가 동일하게 1의 거리를 가질때 로직을 보면 목적지 격자에 도달하기까지 거쳐온 격자의 거리들을 모두 더하는식으로 계산해서 목적지 격자의 값을 리턴합니다. 즉 노란색 + 아래로 내려간 초록색의 값들만 리턴이 되는 것 입니다. 파란색은 목적지 격자에 도달하기 전에 계산이 종료되었으므로 목적지 격자에 파란색 경로나 위로 분기한 초록색 경로의 값은 합산되지 않습니다.

혹시라도 저와 같은 이유로 고민하시는분의 시간이 절약되었으면 합니다.

소스 전체

import java.util.LinkedList;
import java.util.Queue;

// 참고 : https://tmdrl5779.tistory.com/216
@Service
public class GameMapShortPath {

    // 상하좌우 이동을 위한 방향 배열 (0:오른쪽, 1:아래, 2:왼쪽, 3:위)
    int[] dx = {1, 0, -1, 0}; // x축 이동 팩터
    int[] dy = {0, 1, 0, -1}; // y축 이동 팩터

    public int solution(int[][] maps) {
        int answer;

        // 방문 여부 및 최단 거리를 기록할 배열
        int[][] visited = new int[maps.length][maps[0].length];

        // BFS 호출
        bfs(maps, visited);

        // 도착 지점까지의 거리 (방문한 경우 거리 값, 방문하지 못했을 경우 0)
        answer = visited[maps.length - 1][maps[0].length - 1];

        // 도착 지점에 도달하지 못했을 경우 -1 반환
        if (answer == 0) {
            answer = -1;
        }

        return answer;
    }

    // BFS 를 이용해 최단 거리를 찾는 함수
    public void bfs(int[][] maps, int[][] visited) {
        int x = 0;
        int y = 0;

        // 시작점(0, 0) 방문 처리 (거리 1)
        visited[x][y] = 1;

        // BFS 탐색을 위한 큐 (x, y 좌표를 저장)
        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[]{x, y});

        // 큐가 빌 때까지 반복 (탐색할 지점이 없을 때까지)
        while (!queue.isEmpty()) {
            // 큐에서 현재 위치를 꺼냄
            int[] current = queue.remove();
            int cX = current[0]; // 현재 x 좌표
            int cY = current[1]; // 현재 y 좌표

            // 상하좌우로 이동하며 탐색
            for (int i = 0; i < 4; i++) {
                int nX = cX + dx[i]; // 새로운 x 좌표
                int nY = cY + dy[i]; // 새로운 y 좌표

                // 새로운 좌표가 맵을 벗어나면 건너뜀
                if (nX < 0 || nX > maps.length - 1 || nY < 0 || nY > maps[0].length - 1)
                    continue;

                // 아직 방문하지 않았고, 이동할 수 있는 길(1)일 때
                // BFS 에서 이미 방문한 위치는 다시 큐에 추가되지 않기 때문에 최단 거리 계산이 가능
                if (visited[nX][nY] == 0 && maps[nX][nY] == 1) {
                    // 새로운 좌표의 최단 거리는 현재 좌표의 거리 + 1
                    visited[nX][nY] = visited[cX][cY] + 1;
                    // 큐에 새로운 좌표 추가
                    queue.add(new int[]{nX, nY});
                }
            }
        }
    }
}