5. Support Vector Machine(3)

Eony_Jahng·2022년 4월 19일
KOOC인공지능개론1
0

인공지능

목록 보기
10/14

KOOC에서 제공하는 KAIST 문인철 교수님의 "인공지능 및 기계학습 개론 1" 수업입니다.

5.6. Rethinking of SVM

Non-linear Decision Boundary

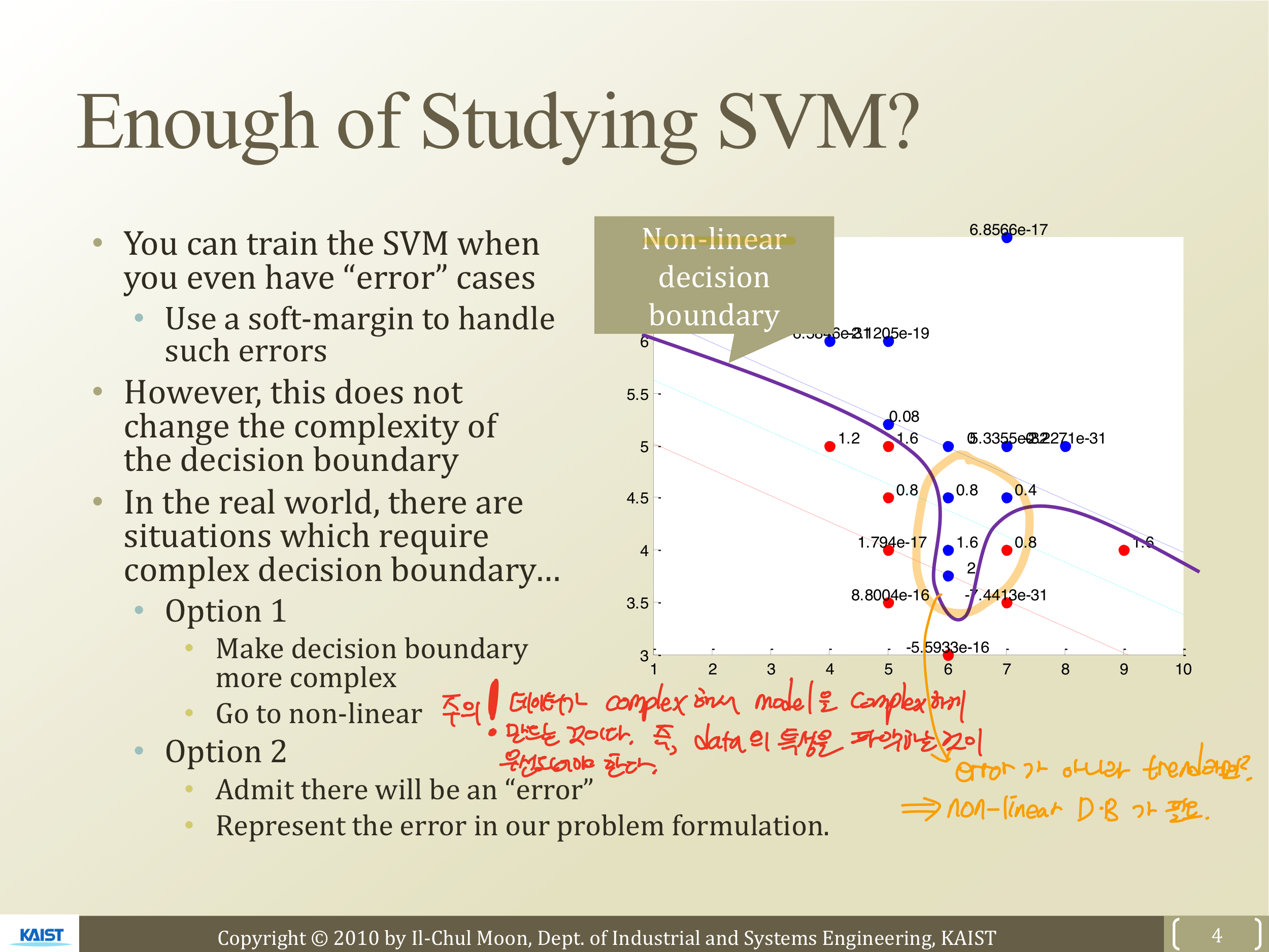
오른쪽 그림과 같이 툭 튀어나와있는 파란점이 있다고 하면, 이 점들은 과연 error case일까 의문을 가져야할 필요가 있어보인다. 이건 주어진 데이터의 특성이지 error가 아닐 것이다. 따라서 D.B를 Non-linear 하게 만들어줘야 할 필요가 있다. 즉, more complex하게 D.B 만드는 방법에 대해서 알아볼 필요가 있다.

이때!! 교수님께서 말씀해주시길, Model을 complex하게 만들기 전에 Data가 complex하기 때문에! 이것을 설명하는 Model을 complex하게 만드는 것임을 알아야한다 고 말씀하십니다. 그래서 우선 주어진 Data의 특성을 파악해서 얼마나 complex하게 만들어야 하는지에 대해 알아보는 과정이 우선적으로 필요하다.

Feature Mapping to Expand Dim

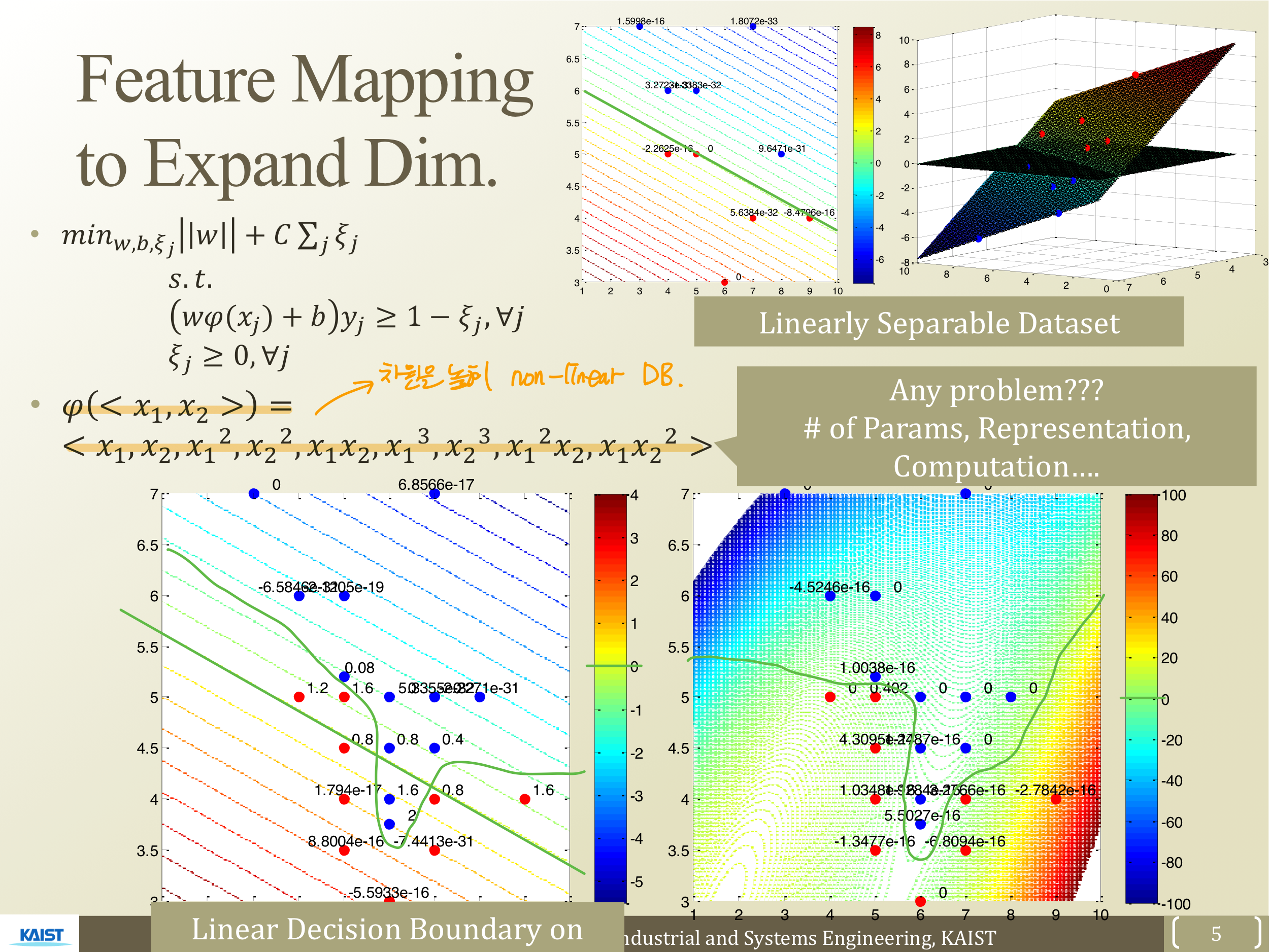
각 데이터를 나타내고 있는 사진과 초록색 선으로 표시된 D.B를 볼 수 있다. 위의 사진과 달리 아래의 사진은 D.B가 Non-linear하게 형성되어 있는 것을 알 수 있는데, 어떻게 하면 D.B를 Non-linear하게 만들 수 있을까?

이는 Linear Regression에서 term 간의 interaction 혹은 term 내부에서 interaction을 만들어서 7차, 8차, ...n차로 복잡한 형태로 Data를 만들어냈던 것을 가져오면 할 수 있다. 즉, 주어진 Data set x1,x2x_1, x_2(각 데이터는 각 축을 의미)의 차원을 높여 표현한다. x1,x2,x12,x22,x1x2...x1x22x_1, x_2, x_1^2, x_2^2,x_1x_2...x_1x_2^2 interaction하면 아래와 같이 Non-linear한 D.B를 만들 수 있다.

이것을 3차보다 더 큰 무한대차원까지 스마트하게 늘리는 방법을 고안한 것이 Kernel이다.

Rethinking the Formulation

Kernel을 쓰기 위해서 Optimization의 성질을 알아야한다. 즉, Quardratic programming에 대해서 이해가 필요하다. Primal problem과 Dual problem 이 두개가 같은 성질을 지닌 두개의 문제로 만들 수 있는 것을 알아야 한다. 인공지능영역보단 Optimization에 가까운 영역인데 더 자세한 내용은 아래의 링크를 참조해 공부해 보았다. 간략하게 개념만 알고 있으면 될 것 같다ㅎㅎ

Duality




Kernel을 도입하기 위해서 SVM Primal problem을 Dual problem로 바꾸면 Kernel 도입이 더 수월하다.

간략하게 말하자면, Lagrange Dual Function을 이용하면 특정 Optimization max⁡α≥0,βL(x,α,β)\max_{\alpha\ge 0, \beta}L(x,\alpha,\beta)를 풀면 f(x)f(x)와 동일하게 동작하는 성질을 갖는다. 즉, Opitmization되어 있는 Lagrange Prime Function인 max⁡α≥0,βL(x,α,β)\max_{\alpha\ge 0, \beta}L(x,\alpha,\beta)을 f(x)f(x)로 대신해서 사용하겠다는 것이다!!

그렇게 하면

min⁡α≥0,βL(x,α,β)→min⁡xmax⁡α≥0,βL(x,α,β)\min_{\alpha\ge0,\beta}L(x,\alpha,\beta) \rightarrow \min_x\max_{\alpha\ge0,\beta}L(x,\alpha,\beta)

이 되는 것!

이렇게 minimum problem을 maximum problem으로 바꿔주는 것이 Kernel을 잘 쓰기 위함이라 했는데...대체 무엇이? 왜?? 어떻게??? 이건 잊지말고 차차 뒤에서 알아보자!

5.7. Primal and Dual with KKT Condition

Primal and Dual Problem

Langrange prime function을 이용해서 primal problem을 dual problem으로 바꿔 주는 것과!! Lagrange Dual Problem을 Lagrange Dual Function을 이용해 Dual Problem으로 표현 한 값은 차이가 있다. 이것을 Dual gap이라 하는데, 그 값은

Dual gap=f(x∗)−d(α∗,β∗)Dual\ gap=f(x^*)-d(\alpha^*,\beta^*)

이다.

그리고 Dual gap이 0이 되는 조건을 Storng duality이라 한다. 즉, Dual func의 solution과 primal func이 같다면(dual problem이 같은 해) Strong Duality가 만족되어야 한다. 그리고 이 조건을 충족하기 위한 필요조건이 존재하는데, 이것을 Karush-Kunh-Tucker (KKT) Conditions이라 한다.

KKT Condition and Strong Duality

KKT Condition은 Primal func을 Dual func으로 만들어 풀기 위한 조건으로, 위의 5가지 조건을 따른다.

Dual Problem of SVM

Hard Margin SVM

min⁡w,b∣∣w∣∣s.t.(wxj+b)yj≥1,∀j\min_{w,b}||w||\\s.t. (wx_j+b)y_j\ge1, \forall j

에서 제약조건 (wxj+b)yj−1=g(x)(wx_j+b)y_j-1=g(x)으로 두고, Langrange method를 적용하면

min⁡w,bmax⁡α≥012ww−∑jαj[(wxj+b)yj−1]s.t.αj≥0,∀j\min_{w,b}\max_{\alpha\ge0}\frac{1}{2}ww-\sum_j\alpha_j[(wx_j+b)y_j-1]\\s.t. \alpha_j\ge0,\forall j

이 된다.

이때 Langrange Prime Function은

L(w,b,α)=f(x)+αg(x)+βh(x)=12ww−∑jαj[(wxj+b)yj−1]L(w,b,\alpha)=f(x)+\alpha g(x)+\beta h(x)\\=\frac{1}{2}ww-\sum_j\alpha_j[(wx_j+b)y_j-1]

이고, Langrange Multiplier은

αj≥0,∀j\alpha_j\ge0,\forall j

가 된다.

Primal problem을 Dual problem으로 바꿔주기 위해 minmin과 maxmax를 바꿔주어,

max⁡α≥0min⁡w,b12ww−∑jαj[(wxj+b)yj−1]s.t.αj≥0,∀j\max_{\alpha\ge0}\min_{w,b}\frac{1}{2}ww-\sum_j\alpha_j[(wx_j+b)y_j-1]\\s.t. \alpha_j\ge0,\forall j

이 된다.

그리고 여기에 KKT Condition을 적용하면 된다. KKT Condition 재료를 준비하면,

∂L(w,b,α)∂w=0, ∂L(w,b,α)∂b=0,\frac{\partial L(w,b,\alpha)}{\partial w}=0,\ \frac{\partial L(w,b,\alpha)}{\partial b}=0,
αi≥0,∀i\alpha_i\ge0,\forall i
αi[(wxj+b)yj−1]=0,∀i\alpha_i[(wx_j+b)y_j-1]=0,\forall i

이 된다.

Dual Representation of SVM

자, 다시 KKT Condition 재료를 정리해보자.

L(w,b,α)=12ww−∑jαj[(wxj+b)yj−1]L(w,b,\alpha)=\frac{1}{2}ww-\sum_j\alpha_j[(wx_j+b)y_j-1]
∂L(w,b,α)∂w=w−∑jαjyjxj=0→w=∑jαjyjxj\frac{\partial L(w,b,\alpha)}{\partial w}=w-\sum_j\alpha_jy_jx_j=0\rightarrow w=\sum_j\alpha_jy_jx_j
∂L(w,b,α)∂b=∑jαjyj=0\frac{\partial L(w,b,\alpha)}{\partial b}=\sum_j\alpha_jy_j=0

KKT Condition 재료는 준비가 되었다. 그럼 이 재료를 Langrange prime function에 대입해 정리하면,

L(w,b,α)=∑jαj−12∑i∑jαiαjyiyjxixjL(w,b,\alpha)=\sum_j\alpha_j-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j

이 된다. 이때 yi,yjy_i,y_j는 우리가 아는 class label이고, xi,xjx_i,x_j는 Input feature이니 위의 Langrange prime function은 α\alpha의 Square term이 된다. 즉!! 다시한번 Quardratic programming이 되는 것이다!!!

Primal problem에서는 w,b에 대해 optimize 했다면, Langrange Dual problem에서는 Langrange multiplier α\alpha를 optimize하는 문제로 바뀐 것이다. α\alpha를 알면 KKT Condition에 의해 ww 값도 알 수 있게 된다. 따라서 α\alpha만 알면 D.B를 recover할 수 있다.

그런데!! 우리는 아직 Linear SVM에 머물러 있다. 왜냐하면 ww라는 것이 Linear D.B의 direction vector 이기 때문인다. 자, 그럼 처음에 가졌던 목적을 다시 생각해보자. 왜 이렇게 primal problem을 dual problem으로 바꾸는 것이 w,b를 찾는 것에 더 좋은 방법일까? 즉 Kernel을 적용하기에 왜 dual problem으로 바꾸는 것이 더 좋은 방법일까? 그것에 대해 알아보자.

5.8. Kernel

Mapping Function

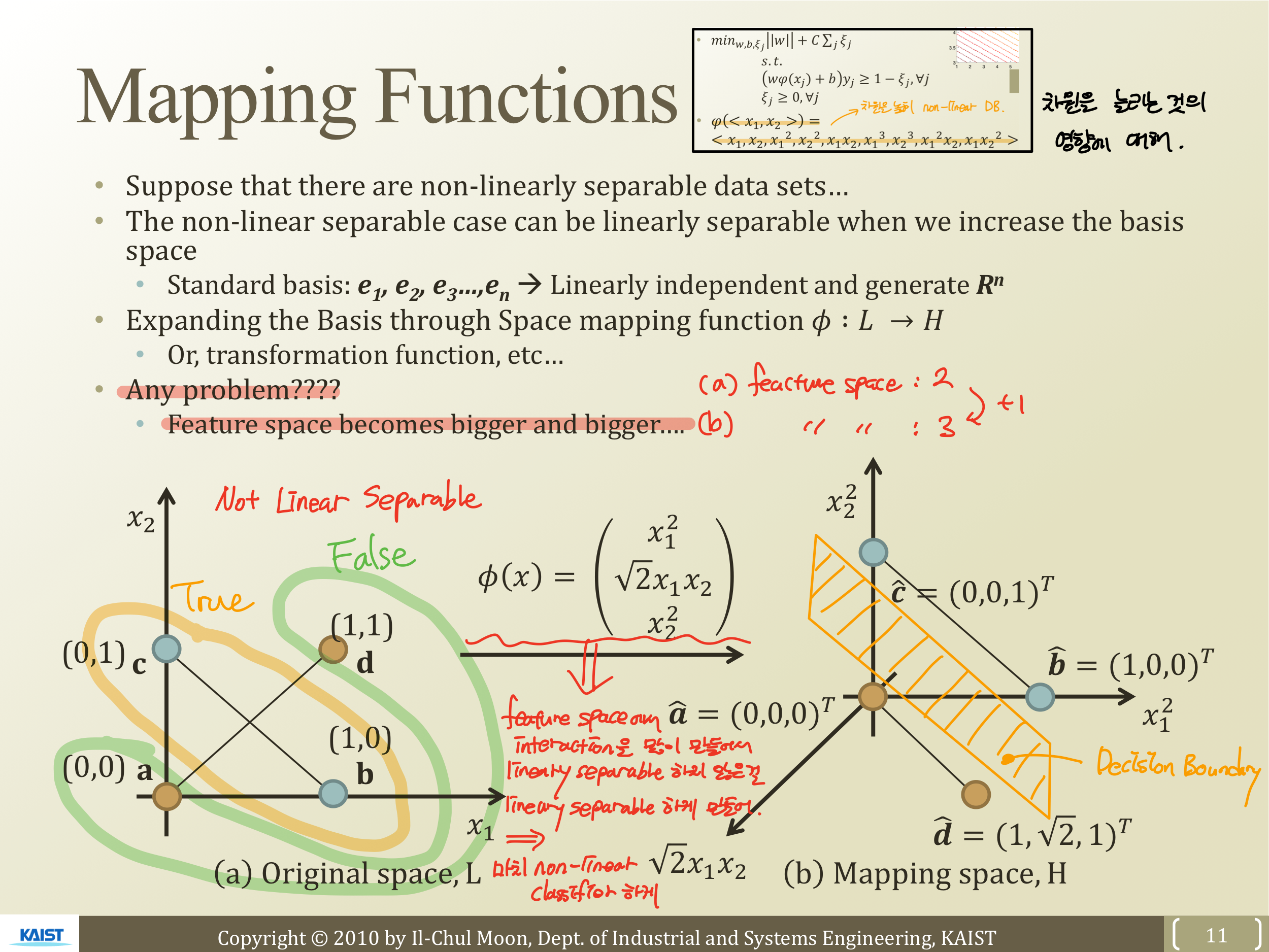
본격적으로 Kernel에 대해 알아보기 전에 높은 차수를 만드는 것이 어떤 영향을 미치는가에 대해 알아본다.

주어진 Original space에 Not Linear Separable한 데이터를 바탕으로 차수를 늘리기 위해 ϕ(x)\phi(x)를 통해 mapping 해주어 차원을 늘려준다.

그 결과는 위의 오른쪽 사진이다. 2 dim에서 not separable한 것이 3 dim 에서 separable 하게 만들 수 있다. 즉, feature space에서 interaction을 많이 만들어주어 linearly separable 하지 않은 것을 linearly separable 하게 만들고, 그다음 linear classifier를 적용해 마치 non-linear classifier 인것처럼 행동하게 만드는 방법이 있다.

하지만 이 방법은 좋지 못하다. 왜냐하면 feature space의 크기가 너무 커지기 때문이다. 그럼 어떻게 해야 Mapping function을 잘 쓸 수 있을까? 하는 의문에서 나온 아이디어가 Kernel이다.

Kernel Function

Kernel calculates the inner product of two vectors in a differenct space.

다른 공간에서 내적inner product라는 말인데, 이때 ψ\psi을 이용해 xix_i를 다른 차원으로 보내고, 그 값의 내적을 Kernel 로 정의한다. 즉,

K(xi,xj)=ψ(xi)⋅ψ(xj)K(x_i,x_j)=\psi(x_i)\cdot\psi(x_j)

이 된다. Kernel의 종류는 다양하다. Polynomial Kernel, Gaussian Kernel, Hyperbolic Kernel 등이 있다. 그 중 Polynomial Kernel에 대해 알아보자.

Polynomial Kernel

위 과정을 살펴보면 차원이 늘어나면서 Polynomial Kernel의 결과가 흥미로운 것을 알 수 있다. <xi,xj><x_i,x_j>를 2차원, 3차원, n차원으로 보내서 내적을 한 것과 먼저 내적을 해서 차원으로 보내는 것이 같다는 것이 Kernel
Function의 특징이다.

두 방법 중 먼저 inner product를 하고 차원을 보내는 것이 더 유리하다. 그 이유는 차원을 보내는 것은 앞에서 봤듯이 feature의 수가 늘어나기 때문에 복잡해진다. 따라서 Kernel Function은 더 높은 차원의 정보를 더 쉽게 다룰 수 있는 기모찌한 방법이다.

5.9. SVM with Kernel

Dual SVM with Kernel Trick

max⁡α≥0∑jαj−12∑i∑jαiαjyiyjxixj\max_{\alpha\ge0}\sum_j\alpha_j-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j

Dual problem이다. 이것을 ψ\psi를 이용해 xi,xjx_i,x_j를 다른 차원으로 보내어 주면,

max⁡α≥0∑jαj−12∑i∑jαiαjyiyjψ(xi)ψ(xj)\max_{\alpha\ge0}\sum_j\alpha_j-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_j\psi(x_i)\psi(x_j)

이 된다. 또 이것을 Kernel로 대체하면,

max⁡α≥0∑jαj−12∑i∑jαiαjyiyjK(xi,xj)\max_{\alpha\ge0}\sum_j\alpha_j-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jK(x_i,x_j)

이 된다. 이제 모든 값을 아니 Dual problem을 maximize하는 α\alpha를 구할 수 있다. 그리고 w,bw, b역시 구할 수 있을 것이다.

w=∑iαiyiψ(xi),b=yj−∑iαiyiψ(xi)ψ(xj)w=\sum_i\alpha_iy_i\psi(x_i),\quad b=y_j-\sum_i\alpha_iy_i\psi(x_i)\psi(x_j)

이때 ww의 ψ(xi)\psi(x_i)는 Kernel 형태가 없다. 여전히 차원을 Mapping하는 형태로 남아있다.

우리가 w,b를 찾는 이유를 다시 생각해보면, w와 b가 있는 func에 input feature x를 넣어 Positive/Negative를 classify하기 위해서 이다. 즉, D.B를 그리는 것이 목적이 아니라 instance의 func 값이 음수인지 양수인지 알아보아 classify하기 위해서이다. 따라서 굳이 w의 값을 정확하게 구할 필요가 없이 결과값만 구해보면 되는 것이다.

Classification with SVM Kernel Trick

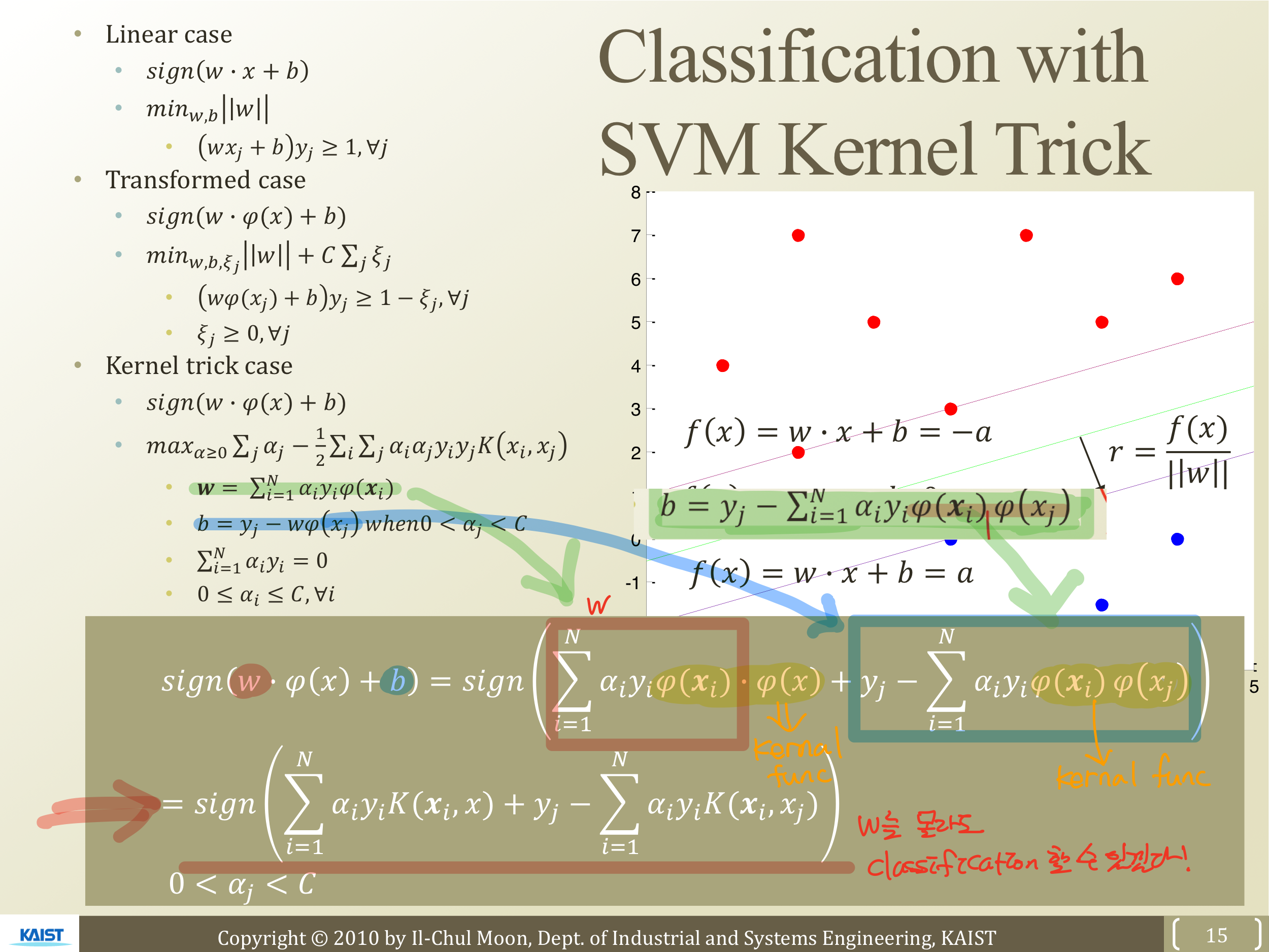
앞으로 들어노는 input feature를 ψ\psi를 이용해 다른 차원으로 보내어 음수인지 양수인지 판단하여 Classify한다 했을 때, w와 b를 알고 있기 때문에 대입하면 위와 같이 나온다.

결국 Kernel func을 이용해 w를 몰라도 calssification 할 수 있다.

단, w 값을 찾아 D.B를 그려보고 하는 것은 불가능하지만 Classification은 가능하다.

profile
Eony_Jahng
7층에 사는 동언이
이전 포스트

5. Support Vector Machine(2)

다음 포스트

6. Training Testing and Regularization(1)

0개의 댓글