KOOC에서 제공하는 KAIST 문인철 교수님의 "인공지능 및 기계학습 개론 2" 수업입니다.

7.4 Bayes Ball Algorithm

Typical Local Structures

Bayesian Network는 Typical한 구조가 있다. 크게 3가지 케이스로 나눠볼 수 있다. 큰 구조안에서 작은 구조라고 생각하면 될 것 같다.

첫 번째, Node가 Common parent를 갖는 경우이다. 이 경우 A를 알면 J와 M은 서로 Independent하다는 것이다.
두 번째, Cascading이다. 각 Node가 단계적으로 일어나는 경우이다. A가 Given인 상황이면, direct influence를 주는 Node에 대한 정보를 알면 그 Node의 Parent에 대한 정보는 불필요하다는 것이다.
세 번째, Node가 Common child를 갖는 경우이다. 이것을 V-structure라고 부른다. 위의 두 경우는 특정 Node의 정보를 알면 다른 Node 간의 관계가 Independent하게 되었다. 하지만 V-structure는 이와 다르게, 특정 node의 정보를 알면 node 간의 관계가 생긴다.

Bayes Ball Algorithm

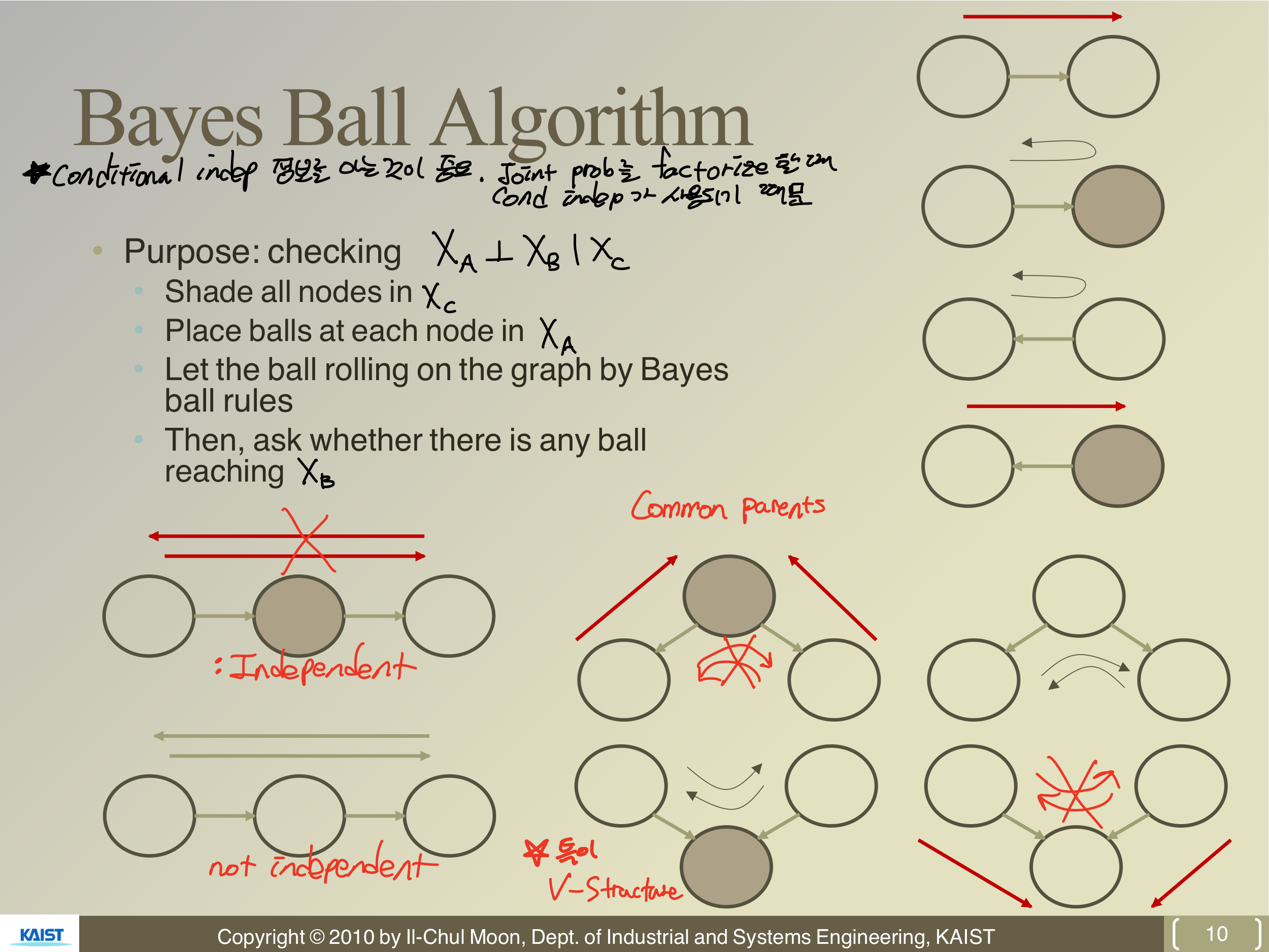
Bayesian Network을 이용해 여러 확률을 분석할 때 conditional independent 정보를 아는 것이 유용하다. 그 이유는 Joint prob를 factorize할 때 conditional independent가 쓰이기 때문이다. 그래서 어떤 정보가 주어졌을 때 independent를 쉽게 판단하기 위한 방법으로 Bayes Ball Algorithm이 쓰인다.

위의 그림에서 색이 칠해진 Node는 관측이 된, 정보를 아는 Node라고 할 때 Variable의 Independent를 판단할 수 있다. 즉, 어떤 특정 random variable의 information이 다른 특정 random variable에 영향을 미치는 지에 대해 표현하는 알고리즘이다.

Exercise of Bayes Ball Algorithm

4가지 케이스에 대해 Independent를 판단할 수 있다면, V-structure에 대해 이해가 됐다고 하자. 그럼 D-Seperation과 Markov Blanket를 정의할 수 있다.

Markov Blanket에 대해 먼저 알아보자. 만약 A라는 Random variable이 Bayesian Network 위에 있다고 가정해보자. 이때 A가 다른 Random variable과 conditional indepent하게 만들어주는 condition이 Markov Blanket이다.

위의 그림에서 A를 제외한 6개의 Random variable을 알면 나머지 6개의 random variable에 대해서 conditional independent하겠다는 것이다. Blanket은 {parents, child, child's parents}로 구성되어 있다. Child's parent는 V-structure 때문에 포함된다.

D-Seperation은 Directly separate의 약자로, Y가 주어진 상황에서 X는 Z와 d-separated된다. 즉 independent하다는 것이다.

7.5 Factorization of Bayesian networks

Factorization of Bayesian Network

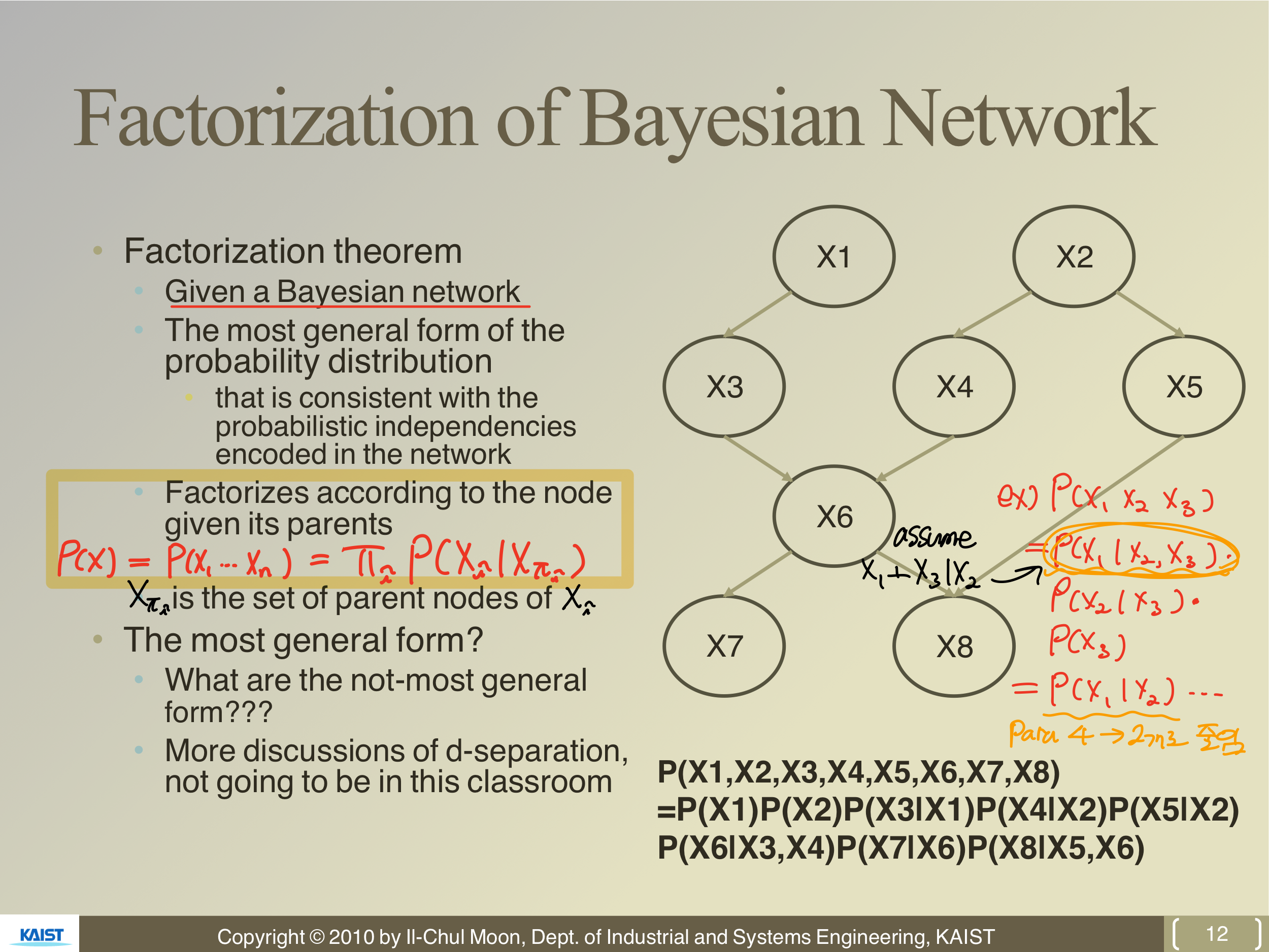
Joint prob를 알면 marginalization을 통해 conditional prob, 개별 indivisual prob를 알 수 있다고 했다. Joint만 알면 되는 것인데, 문제는 Joint prob의 파라미터가 많아 진다는 것이다.

많아진 파라미터를 줄이기 위해서 independent 정보를 알아야 한다. 예를 들어,

Factorize를 통해 위와 같이 정리할 수 있는데, $P(X_1|X_2,X_3)$를 보면 condition이 많다. 이때 만약 $X_3$가 Given인 상황에서 $X_1$과 $X_2$가 conditional independent하다고 가정하면,

가 된다. 즉, 파라미터의 수가 4개(Binary 가정, $X_2,X_3$)에서 2개($X_2$)로 줄었다. 따라서 Bayesian Network에서 Factorization theorem이 중요한 이유는 필요한 정보(파라미터)를 줄일 수 있기 때문이다. Factorization은 다음과 같이 할 수 있다.

이때, $X_{\pi}$는 $X_i$의 parents node를 뜻한다.