시간복잡도란 알고리즘을 푸는데에 있어서 종료할 떄 까지의 시간과 공간을 얼마나 차지하는지의 표기법이다
Big-O
시간복잡도를 계산할 시 발생할 수 있는 최악의 연산 수를 Big-O nation으로 표시할 수 있다. 계산시 작은 상수들을 제외하고 큰 지수들만 표시한다(데이터의 크기가 커질 수록 상수가 성능의 흐름에 크게 상관없어지고, 알고리즘의 러닝타임을 정확하게 표시한다기 보단 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것이 목표이기 때문이다)
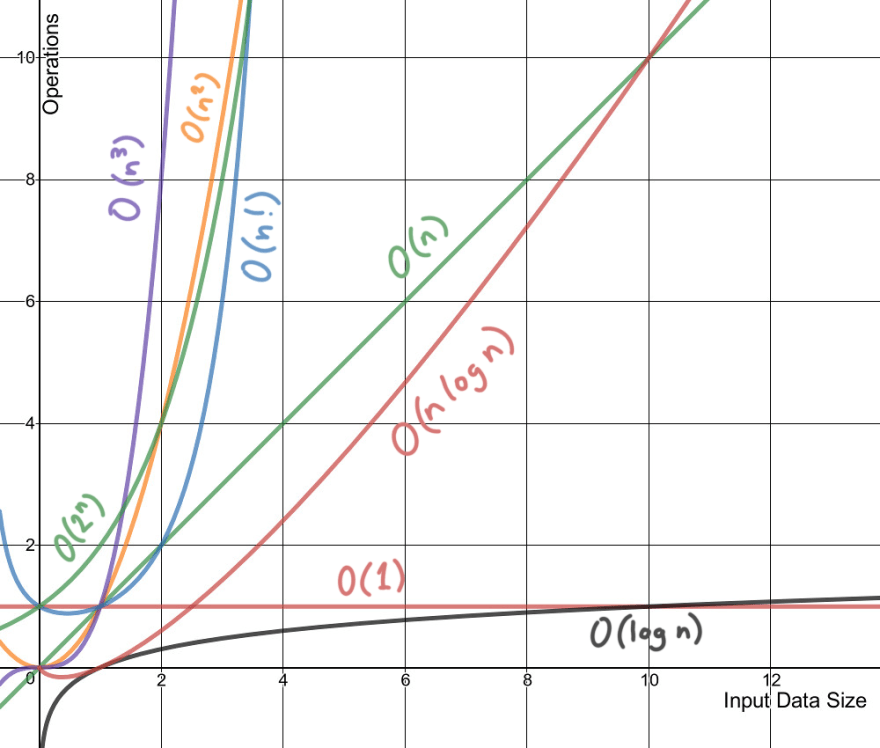
1. O(1) (constant)
입력데이터의 크기에 상관없이 언제나 처리속도는 동행하게 이루어진다.
ex) sorted Array search
2. O(log n) (logarithmic)
입력데이터의 크기가 커지더라도 처리속도가 크게 달라지지 않으며, 실행시간이 지날수록 처리해야 하는 데이터의 양이 절반으로 줄어드며 실행 시간은 증가하지만 속도는 감소한다.
ex) Binary search
3. O(n) (linear)
입력데이터의 크기에 비례해서 처리시간이 증가해 메모리의 사용이 정비례 한다(step : size = 1 : 1).
ex) search linked list, for문을 이용한 array 검색
4. O(n^2) (quadratic)
입력데이터의 크기에 따라 걸리는 시간은 제곱에 비례한다.
ex) 이중 for문
5. O(C^n) (exponential)
문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n제곱이다.
ex) 피보나치 수열, recursion
Big-O 각 자료구조별 시간복잡도 분석
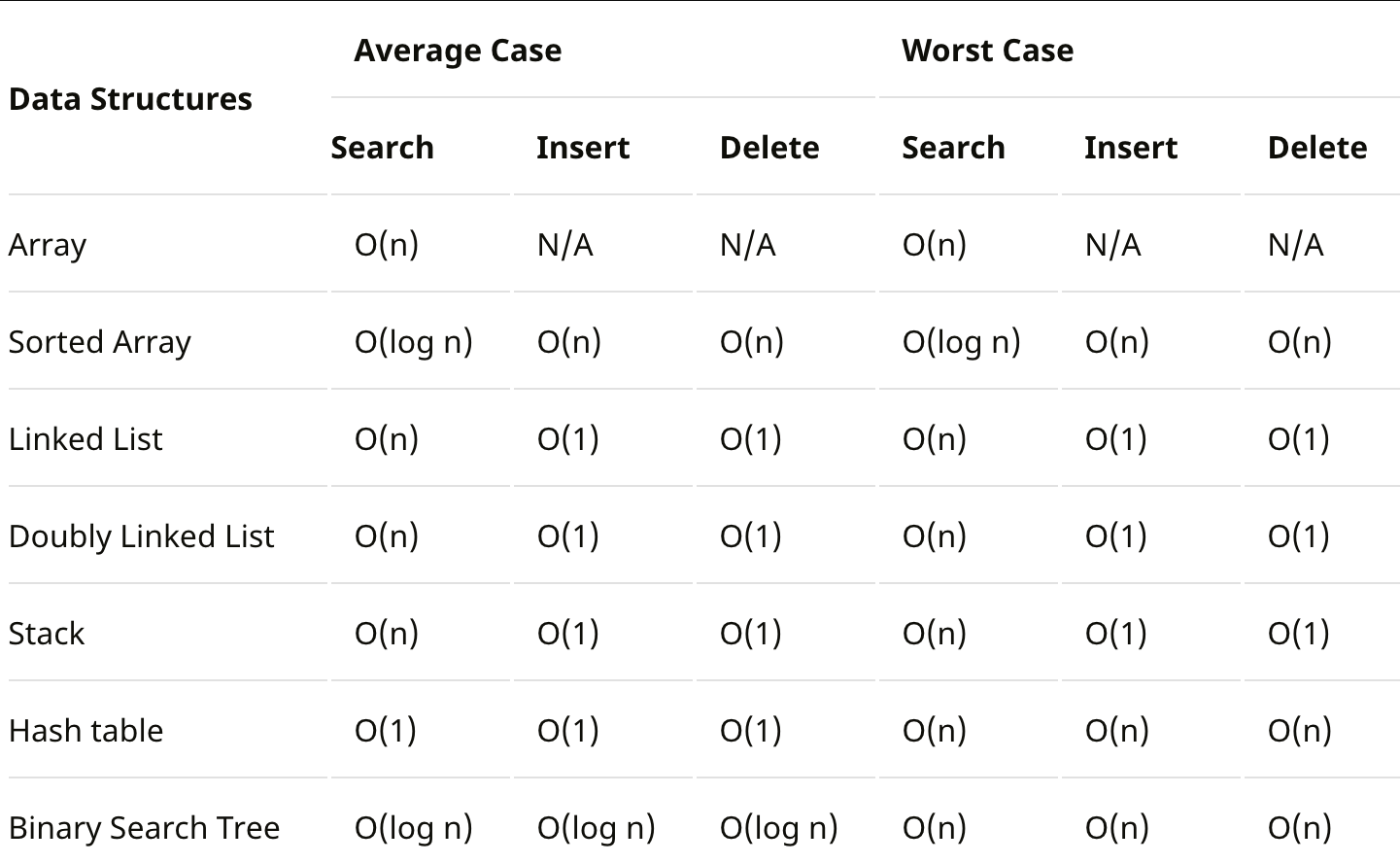
Array
배열은 값 모음을 저장할 수있는 기본 데이터 구조이다(원초적). 메모리 상에서 데이터 공간의 사이즈를 정해주면 그 사이즈를 할당 할 수 있는 공간을 찾아 할당해준다(Javascript 제외)
-
Lookup(position) O(1)
Array에 경우 데이터의 위치를 알고 있기 때문에 검색을 하지않고 바로 접근 할 수 있다. -
Assign O(1)
데이터를 덮어 씌울 때 또한 데이터의 위치를 알고 있기 때문에 바로 접근이 가능하다 -
Insert O(n)
: 데이터를 삽입하려 할 때 그 index의 공간을 확보해야 하기 때문에 다른 데이터들의 자리를 하나씩 옮겨야 한다 -
Remove O(n)
: insert와 마찬가지로 그 index의 데이터를 지우고 공간들을 하나씩 옮겨서 빈공간을 채워야 한다 -
Find O(n)
: 만약 데이터의 위치를 알고 있지 않다면, array의 index를 하나하나씩 살펴보아야 하며 최악의 경우 데이터의 갯수(n)만큼 찾아야 한다
Linked List
Array와 LinkedList의 차이점은 데이터를 저장하는 방식이다. LinkedList는 Array와 같이 데이터가 연속적인 구조가 아니라 랜덤적으로 공간이 배정되어 있다. 따라서 Linked List는 비 연속 데이터 구조이므로 값이 연속 된 블록이 아닌 메모리 전체에 저장된다. Linked List에 경우 head의 노드값을 꼭 알고 있어야 하며, 데이터를 제거할 시 제거하려는 노드의 연결을 끊어주고 그 노드는 garbage collector가 처리한다.
-
Lookup(position) O(n)
Linked List의 경우 random으로 주소를 알고 있기 때문에 바로 접근이 불가능하고 head부터 찾기 시작해야 한다. 따라서 원하는 노드가 나올때까지 찾아야 하며 최악의 경우 데이터의 갯수(n)만큼 검색해야 한다. -
Assign O(n)
: lookup과 마찬가지로 head에서부터 찾기 시작하며 최악의 경우 데이터의 갯수(n)만큼 검색해야 한다. -
Insert O(1)
: 만약 노드를 head 또는 tail에 붙인다면 바로 접근이 가능하다. 따라서 본인의 노드를 head 또는 tail에 연결하면 되므로 시간복잡도는 O(1) 이다
만약 중간에 삽입하는 경우 노드를 삽입하고자 할때 이미 삽입해야하는 위치를 알고 있기 때문에 삽입하고자 하는 노드 전 후를 연결시켜 주면 되므로 시간복잡도가 O(1)이 -
Remove
: 내가 지우고자하는 데이터의 위치를 알고있다 가정하였을 때 insert와 마찬가지로 head와 tail은 시간복잡도가 O(1) 이다
그러나 만약 데이터를 중간에 제거하는 경우 내가 삭제하려는 노드의 위치는 알지만 내 전후의 노드들을 서로 연결시켜줘야 할때 연결하려는 이전 노드를 알지 못하기 때문에 탐색시간이 걸린다(O(n)) -
Find O(n)
: Lookup과 마찬가지로, 첫 노드인 HEAD에서 출발하여 원하는 데이터가 나올 때까지 순서대로 다음 노드들을 살펴봐야 하기에 데이터의 양이 많아질수록 작업 시간이 늘어난다. O(n) -
doubly Linked List
doubly Linked List는 lookup, assign, insert, find의 경우 Linked List와 같이 O(n)이지만, remove의 경우 데이터의 위치를 모두 알고 있기 때문에 검색없이 바로 제거가 가능하다(O(1))
Tree
tree는 시작점인 root노드를 가지며 이어져있는 하위 노드인 children을 가진다. 만약 내가 데이터를 검색해야 한다면 root노드부터 시작하여 내가 원하는 데이터를 찾을때까지 하위 노드를 계속 내려가야한다. 최악의 경우 모든노드의 갯수(n)만큼 살펴보아야 한다.(O(n))
ex) 대표적인 트리구조는 DOM Tree
Binary Search tree
binary Search tree는 자식 노드가 부모노드에 최대 2개씩만 연결되어 있어 왼쪽가지에는 root, 부모노드보다 작은 값, 오른쪽에는 큰 값이 들어 있다.
따라서 검색을 할때 최소의 경우 root노드에서부터 검색을 비교하며 검색을 하지 않아도 되는 노드들은 거치지 않을 수 있기 때문에 검색할 노드에 양이 검색을 할때마다 반씩 줄게 된다 (O(log n))
하지만 Binary Search tree의 종류 중 편향이진트리는 데이터의 구조가 한쪽으로만 치우쳐 있어 Linked List처럼 연결되어 있기 때문에 최악의 경우 노드의 갯수(n)만큼 검색을 해야 한다 (O(n))
