[Data Structure] 해시 테이블 Hash Table

해싱 Hashing

- 데이터를 효율적으로 관리하기 위해 해시 함수를 이용해 
  임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 것
  
- 삽입, 삭제, 탐색 평균 시간 복잡도 O(1)

해시 테이블 Hash Table

해시 함수를 사용하여 변환한 값을 index로 key와 data를 저장하는 자료구조

1. Direct Address Table
   • 가장 간단한 형태의 해시 테이블
   • key 값을 주소로 사용
   • 삽입, 삭제, 탐색 모두 O(1)
   • 한계점
     • 최대 key 값을 알고 있어야 함
     • 최대 key 값이 작을 때 실용적
     • 키 값이 골고루 분포되어있지 않으면 메모리 낭비 심함
2. Hash Table
   
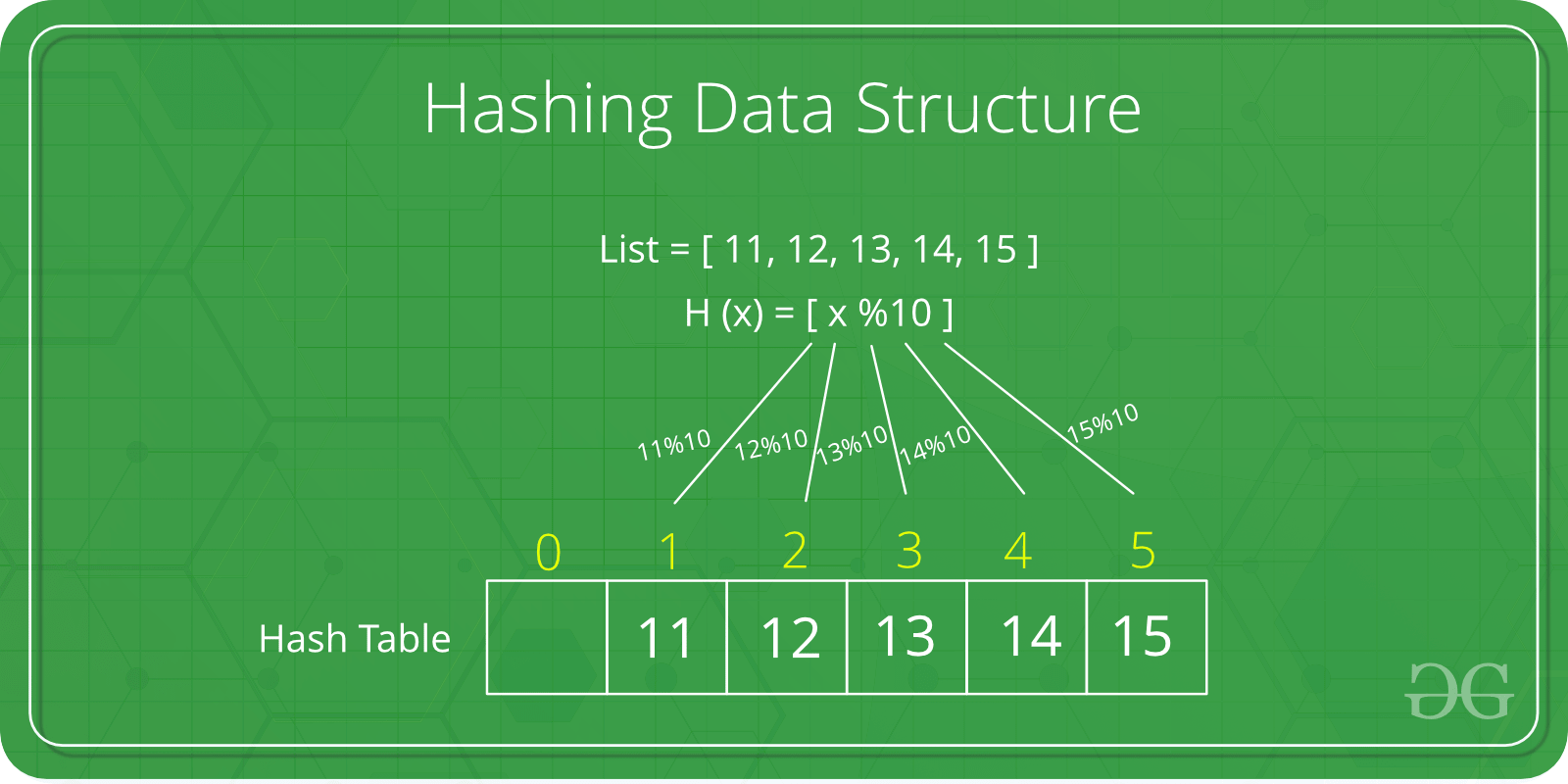
   • 해시 함수를 사용하여 해시 값을 알아내고 그 값을 index로 변환하여 key 값과 data를 저장
   • 충돌 발생 가능성 존재

적재율 Load Factor

- 해시 테이블의 크기 대비 key의 개수
- key의 개수 K, 해시 테이블 크기 N → 적재율 K/N
- 적재율 1 초과시 반드시 충돌 발생
- 충돌 발생 시 탐색/삭제 최악 O(K)
- 충돌을 줄여서 연산 속도를 빠르게 하는 것이 핵심 → 해시 알고리즘이 견고해야 함

충돌 완화 방법

1. 해시 테이블 구조 개선

1. Chaining

- 동일한 버킷에 연결 리스트로 노드를 계속 추가
- 제한 없이 계속 연결 가능하지만 메모리 문제 존재
- 삽입 O(1)
- 탐색/삭제 최악 O(K), 평균 O(적재율+1)

2. Open Addressing

• 해시 함수로 얻은 key 값에 이미 저장된 data가 있으면 다음 주소에 저장

1. 선형 탐사 (Linear Probing): 바로 인접한 인덱스에 삽입, 데이터가 밀집되는 문제 발생 (클러스터링)

2. 제곱 탐사 (Quadratic Probing): 제곱수를 더한 인덱스에 삽입, 초기 해시값 같을 경우 클러스터링

3. 이중 해싱 (Double Hashing): 처음 해시 함수는 해시 값을 찾기 위해 사용, 
   두번째 해시 함수는 충돌 발생 시 탐사 폭 계산을 위해 사용

2. 해시 함수 개선

1. 나눗셈법 (Division Method)

• 간단함
• 미리 해시 테이블의 크기 N을 아는 경우에 사용
• 해시 함수를 적용하고자 하는 값을 N으로 나눈 나머지를 해시 값으로 사용
  $h(k)=k mod N$
• N은 prime number 사용하는 게 좋음

2. 곱셈법 (Multiplication Method)

• 0 < A < 1인 A에 대해서 다음과 같이 구함
  $h(k)=⌊N(kA mod 1)⌋$
• kA의 소수점 이하 부분을 N에 곱함