시작

Problem: 4149번: 큰 수 소인수분해

밀러-라빈 소수판별법과 폴라드 로 알고리즘을 사용하는 문제다.

이 문제를 풀고 나서 10854번, 13926번 등을 쉽게 풀 수 있었다.

밀러 라빈

Miller–Rabin primality test

밀러-라빈 소수판별법은 주어진 수가 소수인지 판별하는 알고리즘 중 하나이다.

특이점으로는, 이 판별법은 확률적인 알고리즘이라는 것이다.

밀러 라빈에 대해 설명하려면 먼저 페르마의 소정리에 대해 알아야 한다.

페르마의 소정리

Fermat's little theorem

소수$p$와 서로소인 정수 $a$에 대해 $a^p \equiv a \pmod {p}$가 만족하며, 다음처럼도 쓸 수 있다.

$a^{p-1} \equiv 1 \pmod {p}$

그리고 이는 모든 소수가 만족하는 필요조건이다. 하지만, 충분조건은 아니다.

---

다시 밀러 라빈으로 돌아와서, $n$이 2가 아닌 소수라고 하면 $n - 1 = 2^sd$가 성립한다. 이 때, $s$는 양의 정수, $d$는 홀수이다.

그리고 위 식은 페르마의 소정리에 의해 다음을 만족하게 된다.

$a^{2^sd} \equiv 1 \pmod n \iff a^{(2^{s-1}d)^2} \equiv 1 \pmod n$

그리고 양변에 루트를 씌우면 다음과 같은 식이 된다.

$a^{2^{s-1}d} \equiv 1 \pmod n \text{ or } a^{2^{s-1}d} \equiv -1 \pmod n$

후자일 경우 $n$은 아마도 소수일 것이고, 전자인 경우 다시 루트를 씌워 다음을 확인해준다.

$a^{2^{s-2}d} \equiv 1 \pmod n \text{ or } a^{2^{s-2}d} \equiv -1 \pmod n$

이런 식으로 반복해서 확인하다 보면 결국 아래의 형태까지 도달하게 된다.

$a^d \equiv 1 \pmod n \text{ or } a^d \equiv -1 \pmod n$

해당 과정에서 위 합동식이 하나도 성립하지 않았다면 $a$는 소수가 아님이 확실하며, 한 번이라도 성립했다면 $a$는 확률적으로 소수라고 할 수 있다.

마지막으로 정리해보면, $n$이 소수인 경우 다음 두 합동식 중 하나가 성립한다.

$a^d \equiv 1 \pmod n$

$a^{2^rd} \equiv -1 \pmod n \quad for\; some \; r \quad (0 \leq r < s)$

식이 성립할 때, $n$은 확률적 소수(probable prime)라고 한다.

만약 식이 하나도 성립하지 않을 경우 $n$은 확실한 합성수이며, 이 때 $a$는 $n$의 합성에 대한 증거(witness)라고 한다.

그런데 위에서도 설명했듯이 이 판별법은 확률적인 알고리즘이다.

그렇기에 이 판별식에서 합성수인 $n$이 특정한 $a$에 대해 합동식을 만족할 수도 있다.

만약 그럴 경우, $n$은 강한 의사 소수(strong pseudoprime)라고 하며, $a$는 강한 거짓증거(strong liar)라고 한다.

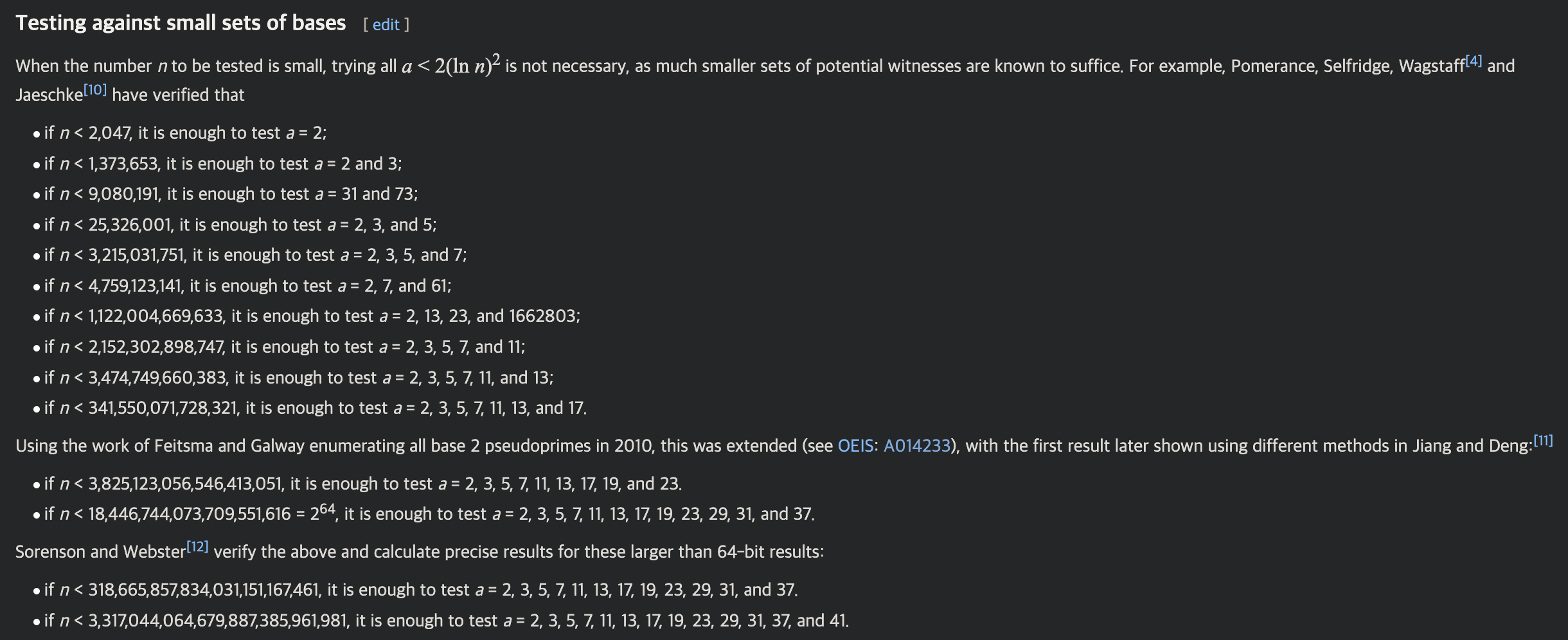
따라서 $n$이 소수일 것을 단정짓기 위해 사진처럼 $n$의 크기에 따라서 이 정도까지만 확인해보면 충분하다는 $a$의 목록이 있다.

이번 문제에서 $n$의 크기는 $2^{62} = 4,611,686,018,427,387,904$

즉 37까지만 확인하면 충분하다고 한다.

폴라드 로

Pollard's rho algorithm

폴라드 로 알고리즘은 대략 $O(\sqrt[4]n)$의 시간복잡도를 갖는 소인수분해 알고리즘이다.

$g(x) = x^2 + c \pmod n$에 대해 초항($x_0$)과 상수항($c$)을 임의로 정하고 아래와 같은 수열을 정의해보자.

$x_k = x_0, g(x_0), g((x_0)), g(((x_0))) ...$

그리고 $n$의 인수인 $p$에 대해 $\{x_k \bmod p\}$ 라는 수열도 정의해보자.

위의 두 수열은 모두 어느 한 순간부터 반복된다.

두 정점 $i$, $j$($x_i$와 $x_j$)를 정하고, 토끼와 거북이 알고리즘을 활용하여 매 단계마다 하나는 1씩, 다른 하나는 2씩 증가하게 한다.

그 후 $gcd(|x_i - x_j|, n)$을 확인하여 1이 아니라면 수열 $\{x_k \bmod p\}$은 반복된다는 것을 의미한다.

만약 최대공약수가 $n$이라면 수열 $\{x_k\}$을 한 바퀴 돌았음에도 소인수를 찾지 못했다는 것이니 초항과 상수항을 바꿔서 다시 알고리즘을 돌리면 된다.

문제 풀이

def powmod(a, e, m):
    ret = 1
    t = a % m
    while e > 0:
        if e & 1:
            ret = ret * t % m
        t = t * t % m
        e >>= 1
    return ret

거듭제곱과 나머지 연산을 빠르게 할 수 있는 Modular exponentiation을 사용했다.

if e & 1:부분은 비트 연산자를 이용해서 홀수/짝수를 판별하는 과정이다.

e >>= 1도 비트 연산자로, e //= 2와 같은 뜻이다.

def miller_rabin(n, a):
    d = n - 1
    while d % 2 == 0:
        if powmod(a, d, n) == n - 1:
            return True
        d //= 2
    t = powmod(a, d, n)
    return t == n - 1 or t == 1


def is_prime(n):
    if n == 1 or n % 2 == 0:
        return False

    for a in [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]:
        if n == a:
            return True
        if not miller_rabin(n, a):
            return False
    return True

밀러 라빈 알고리즘을 이용해서 만든 소수 판별 함수이다.

앞서 설명했듯이 37까지만 확인하면 충분하다고 하니 그대로 사용했다.

def pollard_rho(n):
    if is_prime(n):
        return n

    if n == 1:
        return 1
    if n % 2 == 0:
        return 2

    x = randrange(2, n)
    y = x
    c = randrange(1, n)
    d = 1

    while d == 1:
        x = ((x ** 2 % n) + c + n) % n
        y = ((y ** 2 % n) + c + n) % n
        y = ((y ** 2 % n) + c + n) % n
        d = gcd(abs(x - y), n)

        if d == n:
            return pollard_rho(n)
    if is_prime(d):
        return d
    return pollard_rho(d)

$n$이 소수일 경우 알고리즘이 매우 느려지니 처음에 위에서 정의한 is_prime함수를 사용해서 소수인 경우를 처리해주었다.

while n > 1:
    d = pollard_rho(n)
    l.append(d)
    n //= d
l.sort()

단순히 리스트 l에 소인수들을 저장해주는 과정이다.

전체 소스

from sys import stdin, setrecursionlimit
from math import gcd
from random import randrange

setrecursionlimit(10 ** 4)
input = stdin.readline


def powmod(a, e, m):
    ret = 1
    t = a % m
    while e > 0:
        if e & 1:
            ret = ret * t % m
        t = t * t % m
        e >>= 1
    return ret


def miller_rabin(n, a):
    d = n - 1
    while d % 2 == 0:
        if powmod(a, d, n) == n - 1:
            return True
        d //= 2
    t = powmod(a, d, n)
    return t == n - 1 or t == 1


def is_prime(n):
    if n == 1 or n % 2 == 0:
        return False

    for a in [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]:
        if n == a:
            return True
        if not miller_rabin(n, a):
            return False
    return True


def pollard_rho(n):
    if is_prime(n):
        return n

    if n == 1:
        return 1
    if n % 2 == 0:
        return 2

    x = randrange(2, n)
    y = x
    c = randrange(1, n)
    d = 1

    while d == 1:
        x = ((x ** 2 % n) + c + n) % n
        y = ((y ** 2 % n) + c + n) % n
        y = ((y ** 2 % n) + c + n) % n
        d = gcd(abs(x - y), n)

        if d == n:
            return pollard_rho(n)
    if is_prime(d):
        return d
    return pollard_rho(d)


n = int(input())
l = []

while n > 1:
    d = pollard_rho(n)
    l.append(d)
    n //= d
l.sort()

print(*l, sep="\n")

끝

확실히 블로그에 정리하면서 복습이 잘 되는듯