조건
나에게 주어진 물건들이 있고 각각의 물건은 무게와 가치가 다르다.
이 물건들을 무게가 한정된 배낭안에 최대의 가치로 넣는 알고리즘을 KnapSack 알고리즘이라 부른다.
풀이법
1. 브루트포스 (Brute Force)
만약 3개의 물건이 있다고 가정하자.
각각의 물건을 넣는 경우와 넣지 않는 경우가 있으므로 경우의 수는 총 2^3이다.
즉, 물건의 개수가 N개라면 총 경우의 수 (시간 복잡도)는 2^N이 되므로 효율적이지 못하다.
2. 다이나믹 프로그래밍 (DP)
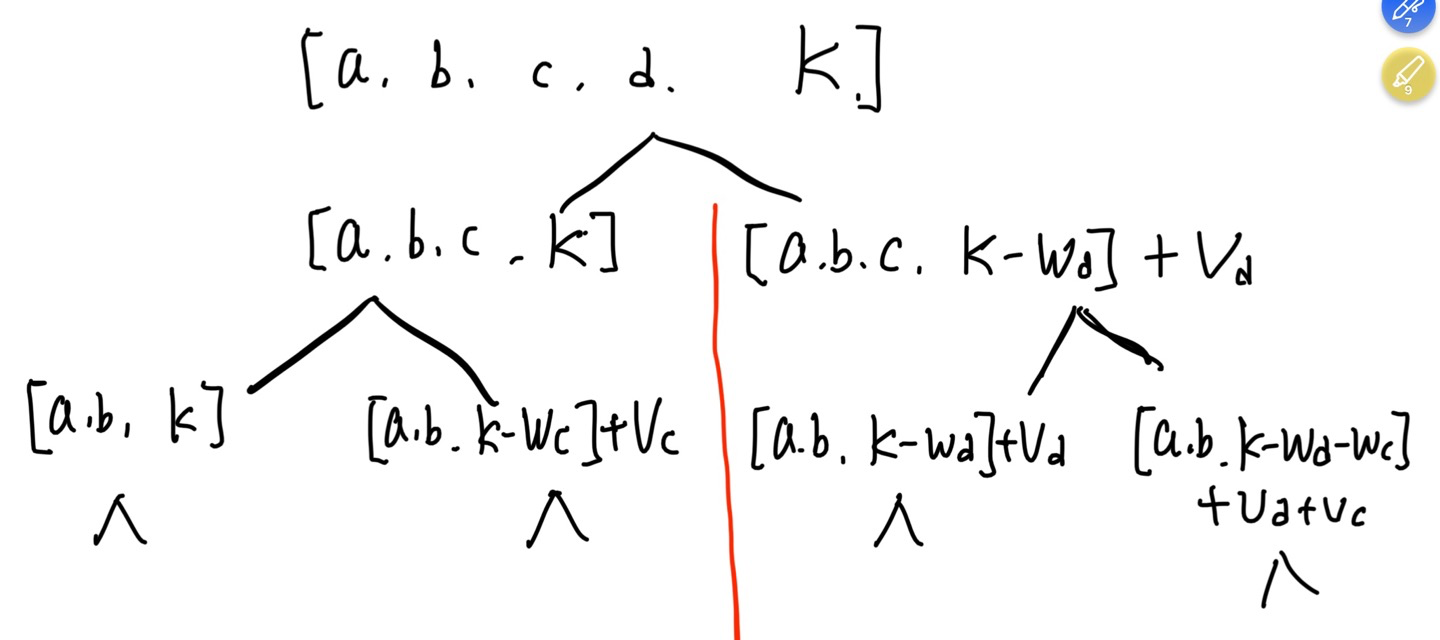
DP를 위한 가지치기를 시작해보자.
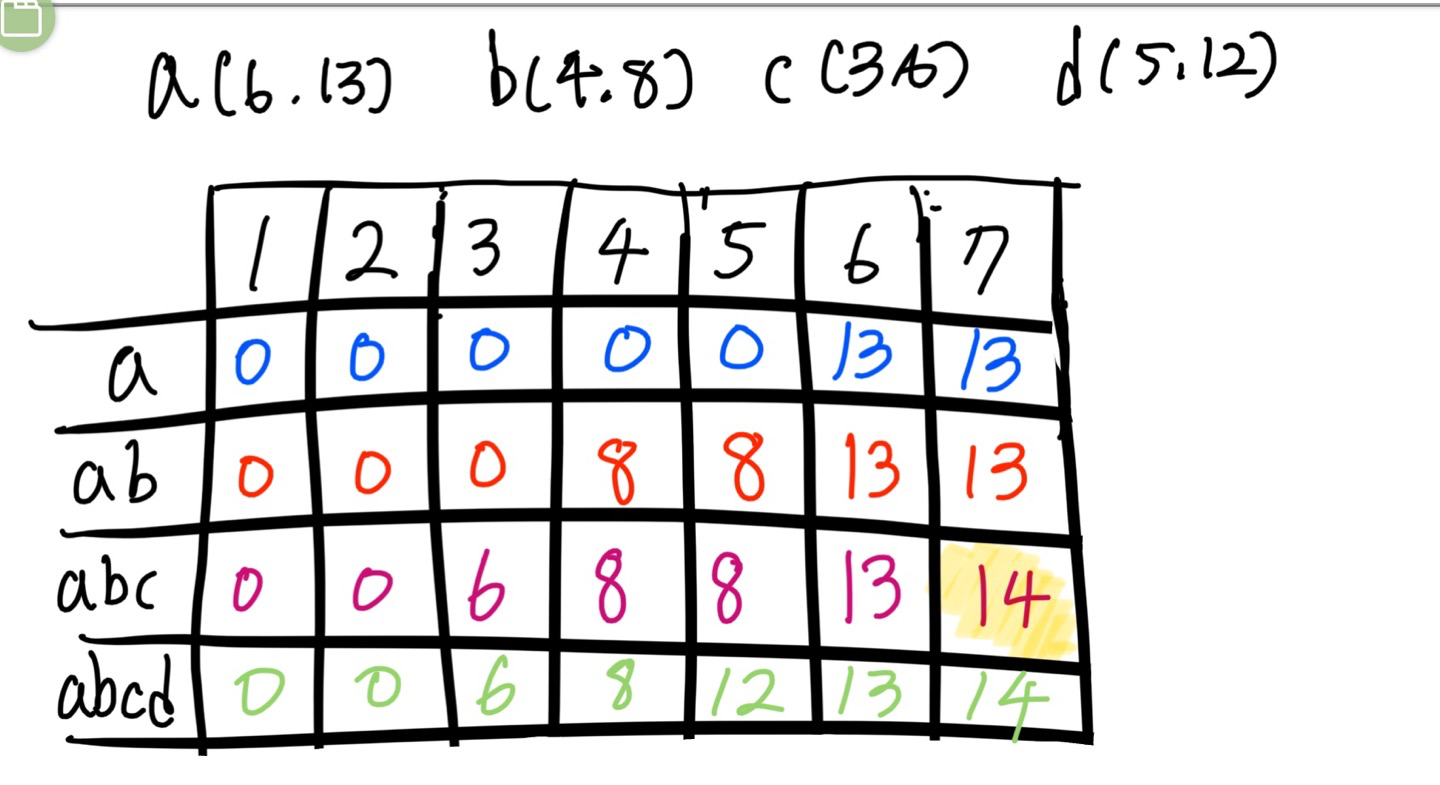
a,b,c,d 물건 4개가 있고 배낭에 넣을 수 있는 총 무게는 K이다.
- 물건 d를 배낭에 넣는 경우와 넣지 않는 경우로 나눈다.
- 배낭에 넣지 않은 경우 배낭에 넣을 수 있는 무게는 여전히 K이다.
- 배낭에 넣은 경우 배낭에 넣을 수 있는 무게는 (K - d의 무게)이고 현재 가치는 d의 값이다.
위의 그림만 보면 이해가 잘 안되니 한번 표를 그려보자.
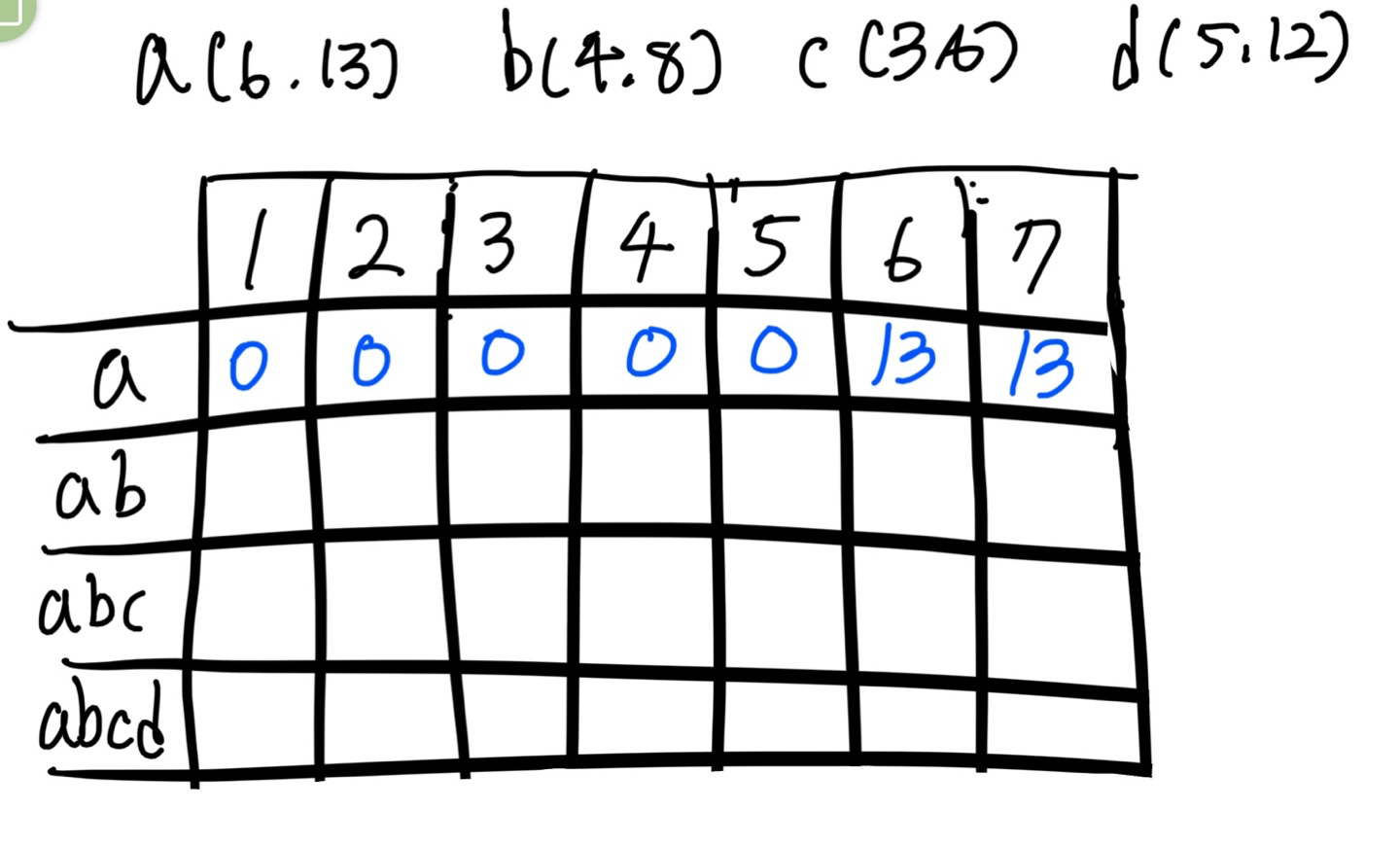
a,b,c,d 물건 4개가 있고 각각의 물건은 무게와 가치를 가지고 있다.
그리고 총 무게 1부터 7을 버틸 수 있는 배낭(배열)이 있다.
이때 물건을 하나하나 추가하면서 dp배열에 넣을 수 있는 최대 가치를 구할 것임.
-
물건 a만 넣는 경우
1-1. 물건 a의 무게는 6이므로 배낭에 1부터 5까지는 값이 못들어감.
1-2. 6부터 7까지는 물건 a의 가치인 13이 배열에 저장된다.
-
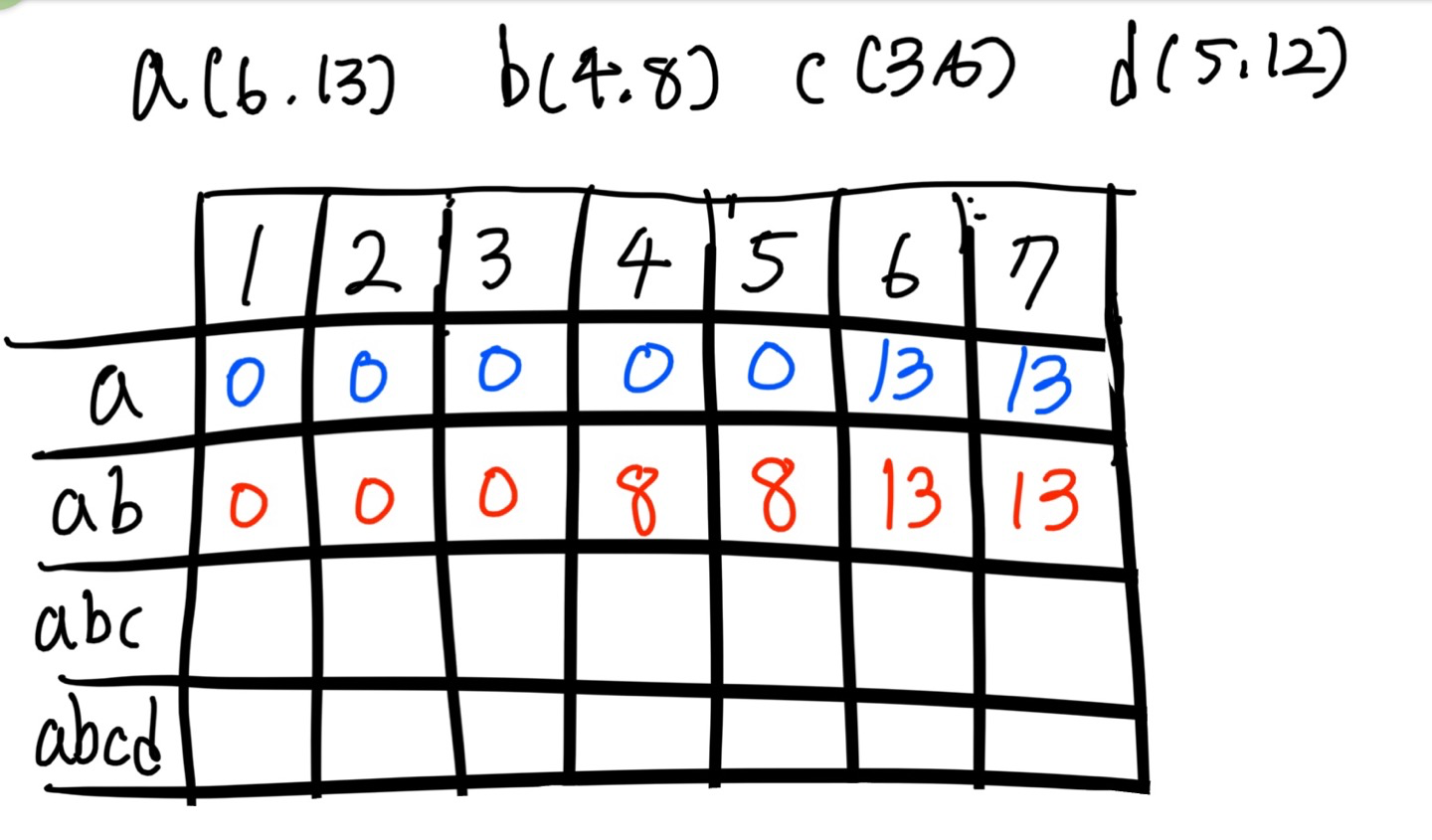
물건 a 또는 b를 넣는 경우
2-0. a,b 둘을 넣으면 배낭 무게를 초과하므로 한개씩 밖에 못넣음.
2-1. 1부터 3까지는 a,b 무게 모두 3을 초과하므로 값을 넣을 수 없다.
2-2. 4부터 5까지는 a를 넣지 못하고 b만 넣을 수 있으므로 값은 8임.
2-3. 6부터 7까지는 a의 가치가 b의 가치보다 높으므로 값은 13임.
-
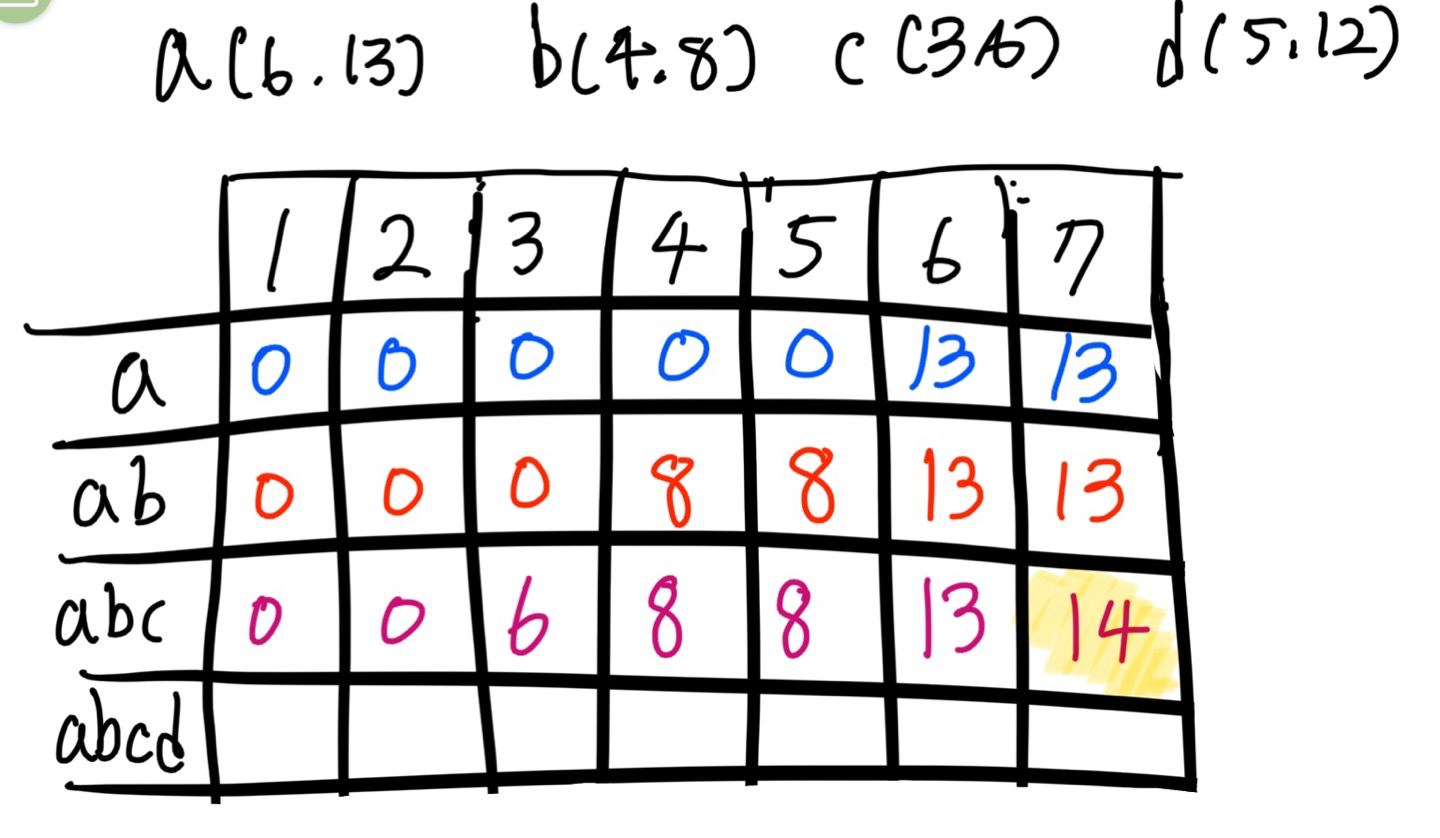
물건 a 또는 b 또는 c를 넣는 경우
3-1. 1부터 2까지는 아무것도 넣을 수 없다.
3-2. c의 무게가 3이므로 세번째칸에 c만 넣을 수 있음.
3-3. 4부터 5까지는 c의 가치보다 b의 가치가 더 크므로 8을 넣는다.
3-4. 6번째 칸은 a의 가치가 가장 크므로 13이다.
3-5. 7번째 칸은 b와 c의 조합이 가능하다. 이때 조합한 값 14가 13보다 크므로 14로 체인지
3-5의 과정에서 점화식 유추가 가능했다. 배낭에 채울수 있는 무게가 7인데 우선 c를 넣어 배낭을 채운다. 그렇게 되면 배낭에 넣을 수 있는 무게는 (7-3)=4가 된다.
이를 통해 배낭의 남은 무게가 4인 라인(dp[4]) 중 c를 넣기 직전 값(그게 최대값이므로)을 찾으면 된다. 그러면 배낭에 넣을 수 있는 무게는 [c를 넣지 않은 dp[4]] + [c의 무게]가 된다. 따라서 가치의 합은 14가 되고 14는 13보다 크므로 14로 dp에 값을 저장한다.
(설명이 너무 어렵다..)
- 모두 사용 가능
이를 토대로 점화식을 만들면
1. i번째 물건이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 물건을 뺀 i-1개의 물건들을 가지고 구한 전 단계의 최대값을 가져온다.
2. 그렇지 않은 경우, 배낭에 i번째 물건만큼의 무게를 비웠을 때의 최대값에 i번째 물건의 가치를 더한 값 or i-1개의 물건들을 가지고 구한 전 단계의 최대값 중 큰 것을 선택한다.
코드
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int [] w = new int[N+1];
int [] v = new int[N+1];
int [][] dp = new int[N+1][K+1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
w[i] = Integer.parseInt(st.nextToken());
v[i] = Integer.parseInt(st.nextToken());
}
for (int i = 1; i<=N; i++) {
for (int j = 1; j<=K; j++) {
if(w[i]>j) {
dp[i][j] = dp[i-1][j];
}
else {
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-w[i]] + v[i];
}
}
}
System.out.println(dp[N][K]);
