백준 1010 - 다리 놓기

---

링크

https://www.acmicpc.net/problem/1010

---

조건

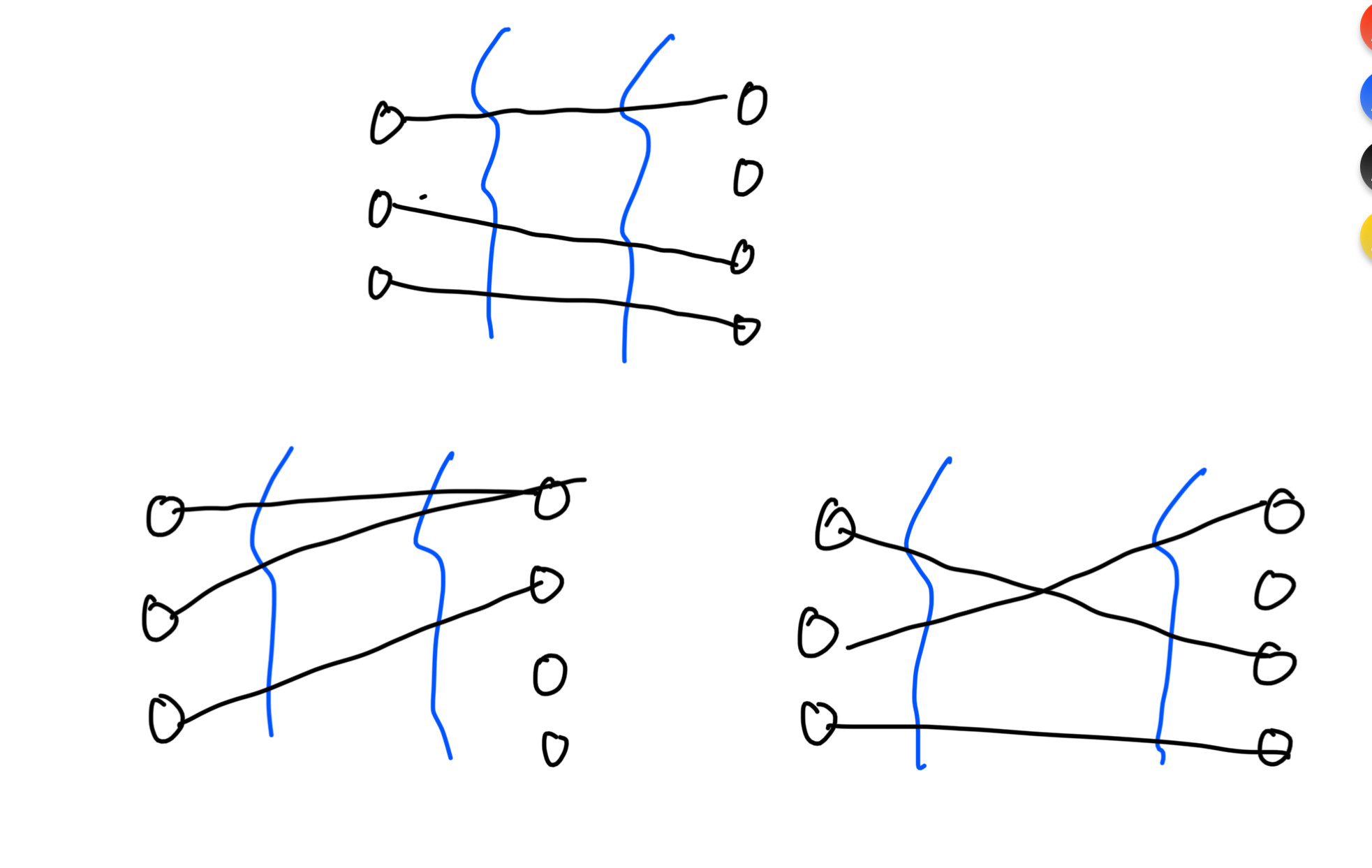
1. 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다. (N ≤ M)
2. N개의 다리를 지어야 한다.
3. 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.
   1. 한 사이트는 한번만 선택 가능하다는 의미 → 즉, 중복이 불가능하다.
4. 다리끼리는 서로 겹쳐질 수 없다.

---

접근법

1. M개의 사이트 중 N개의 사이트를 뽑는 느낌 → 조합
2. 조합만하면 느낌상 뭔가 교차되는 다리는 고려안하는 느낌인데..
3. 조합은 아래의 경우가 모두 하나의 동일한 경우의 수이다. (순서는 고려하지 않으므로)

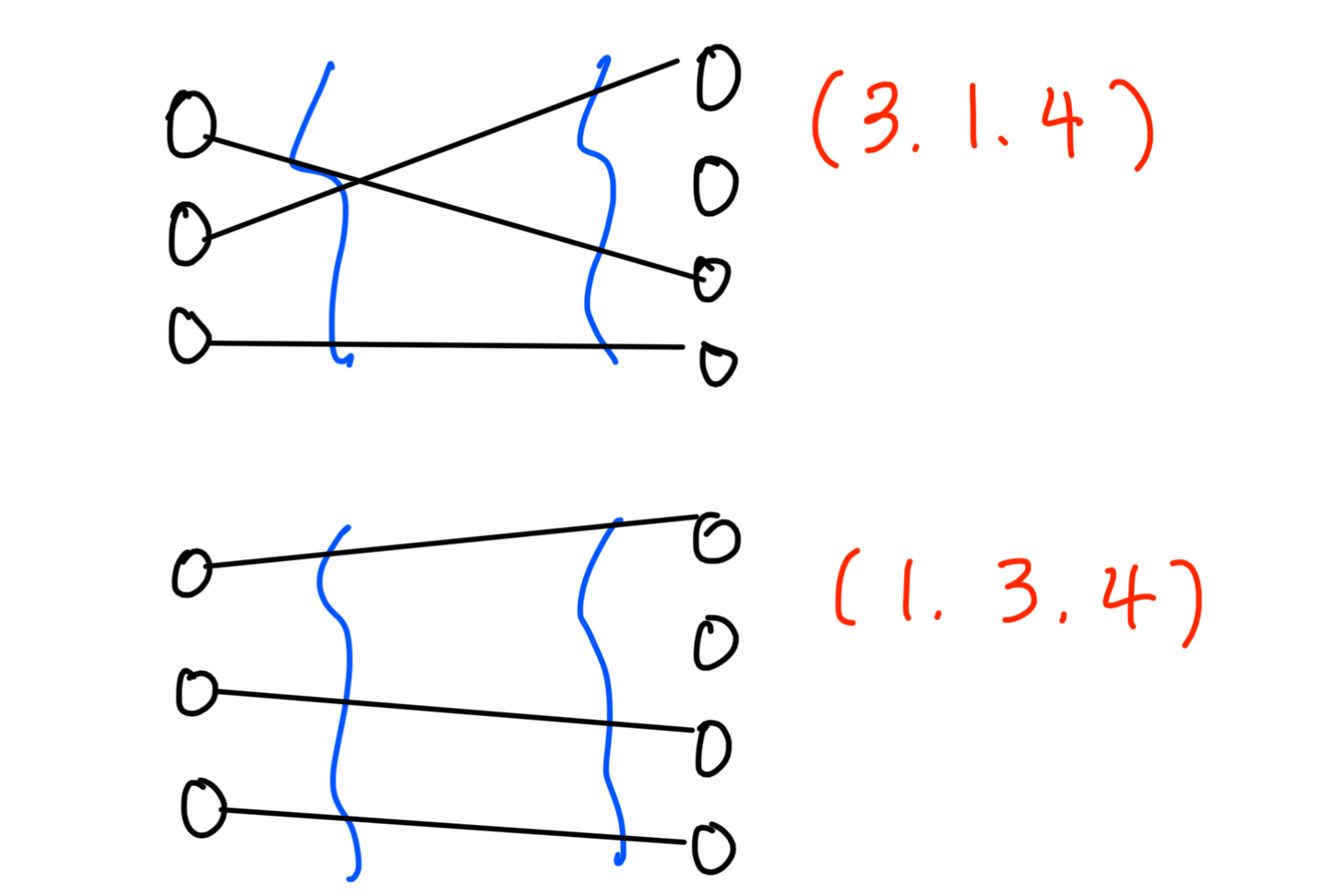
4. 결국, 조합을 통해 뽑을 시 자연스럽게 다리가 교차된 경우는 제외된다.

---

풀이1

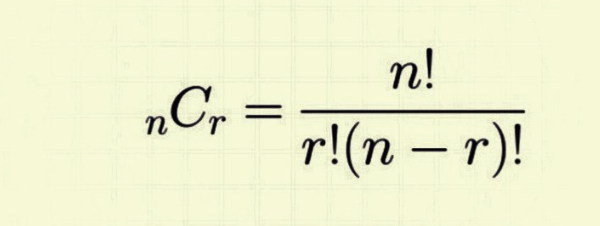
public class Problem1010_2 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        int T = Integer.parseInt(br.readLine());

        for (int i = 0; i < T; i++) {
            st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            int M = Integer.parseInt(st.nextToken());
            System.out.println(combination(M, N));
        }
    }

    public static long combination(int n, int r) {
        long a = 1;
        long b = 1;

        for (long i = n; i > n - r; i--) {
            a = a * i;
        }
        for (long i = r; i > 0; i--) {
            b = b * i;
        }
        
        return a / b;
    }

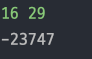
• 29C16 에서 long 타입의 최대값을 넘어가 오버플로우 발생
• 15! → int 초과
• 21! → long 초과
• 다른 풀이법을 찾아야 한다.

---

풀이2

• 조합의 성질 (nCr)
  • r 이 0이면 1
  • n 과 r 이 같으면 1
    

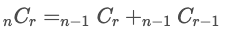
public class Problem1010 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        int T = Integer.parseInt(br.readLine());
        
		// N과 M의 범위가 30까지이므로 크기가 30X30인 조합을 나타내는 이차원 배열 생성
        // 즉, 3C2라 하면 arr[3][2]가 되는 것!
        int[][] arr = new int[30][30];
        
   	    // 0C0은 1이다
        arr[0][0] = 1;

        for (int i = 1; i < 30; i++) {
            for (int j = 0; j < 30; j++) {
                if (j == 0) {
                    arr[i][j] = 1;
                    continue;
                }
                if (i == j) {
                    arr[i][j] = 1;
                    continue;
                }

                arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
            }
        }

        for (int i = 0; i < T; i++) {
            st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            int M = Integer.parseInt(st.nextToken());
            System.out.println(arr[M][N]);
        }

    }
}

• 위와 같은 dp형식으로 풀면 long 타입으로 연산 시 66C33 까지 가능![]