정의

최장 증가 부분 수열(Longest Increasing Subsequence)
특정 수열에서 오름차순으로 정렬된 가장 긴 부분 수열을 찾는 알고리즘이다.
이 때, 오름차순으로 정렬된 부분이 비연속적일 수 있다.

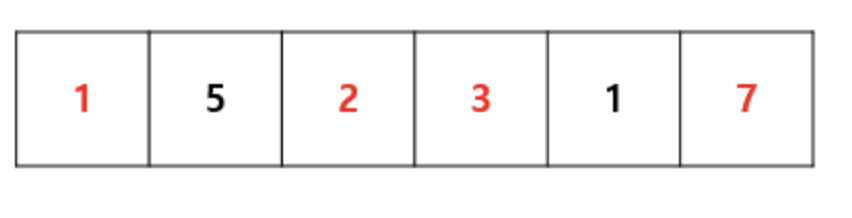https://sskl660.tistory.com/89
위의 배열에서 LIS는 1,2,3,7이다.

풀이 - 동적계획법

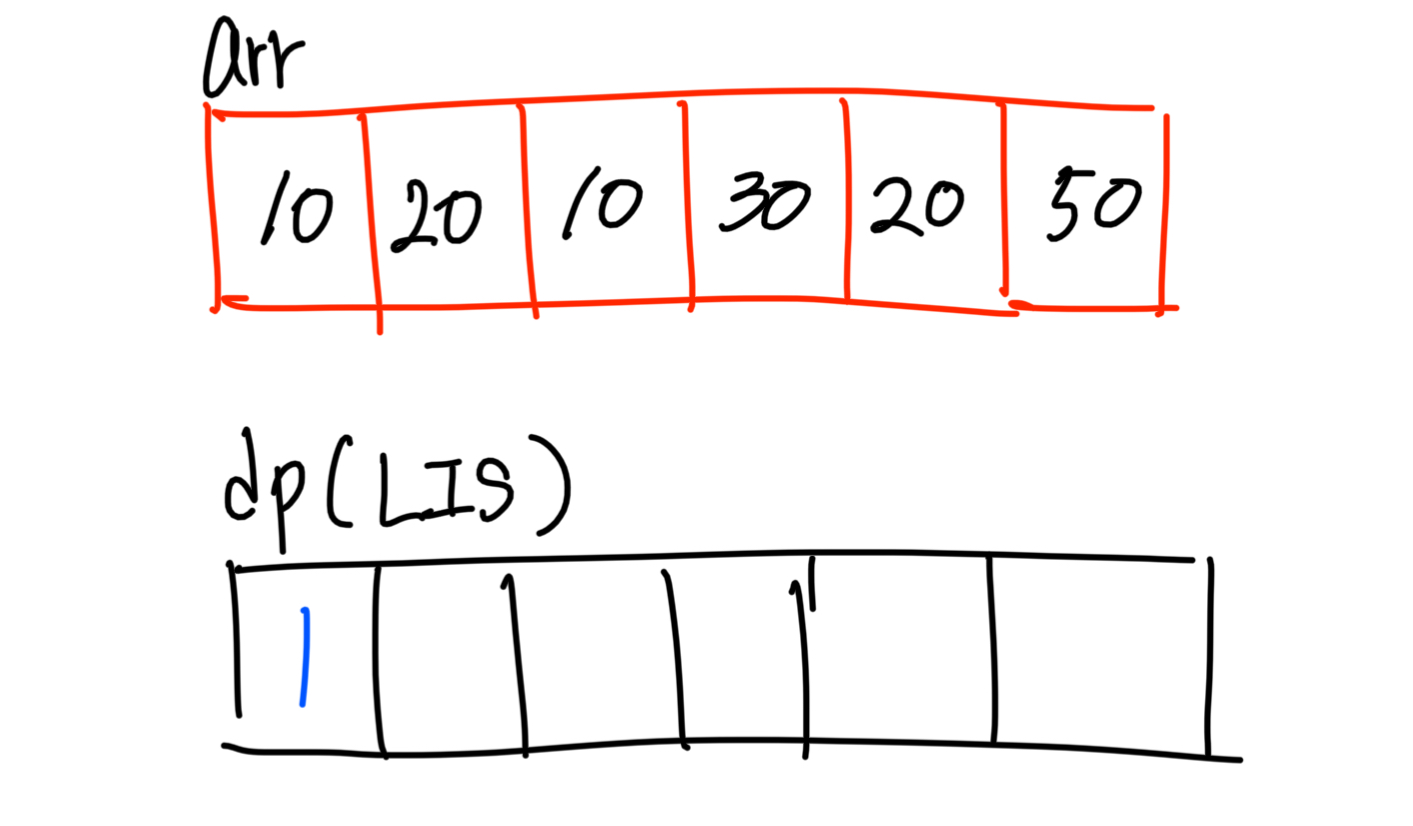
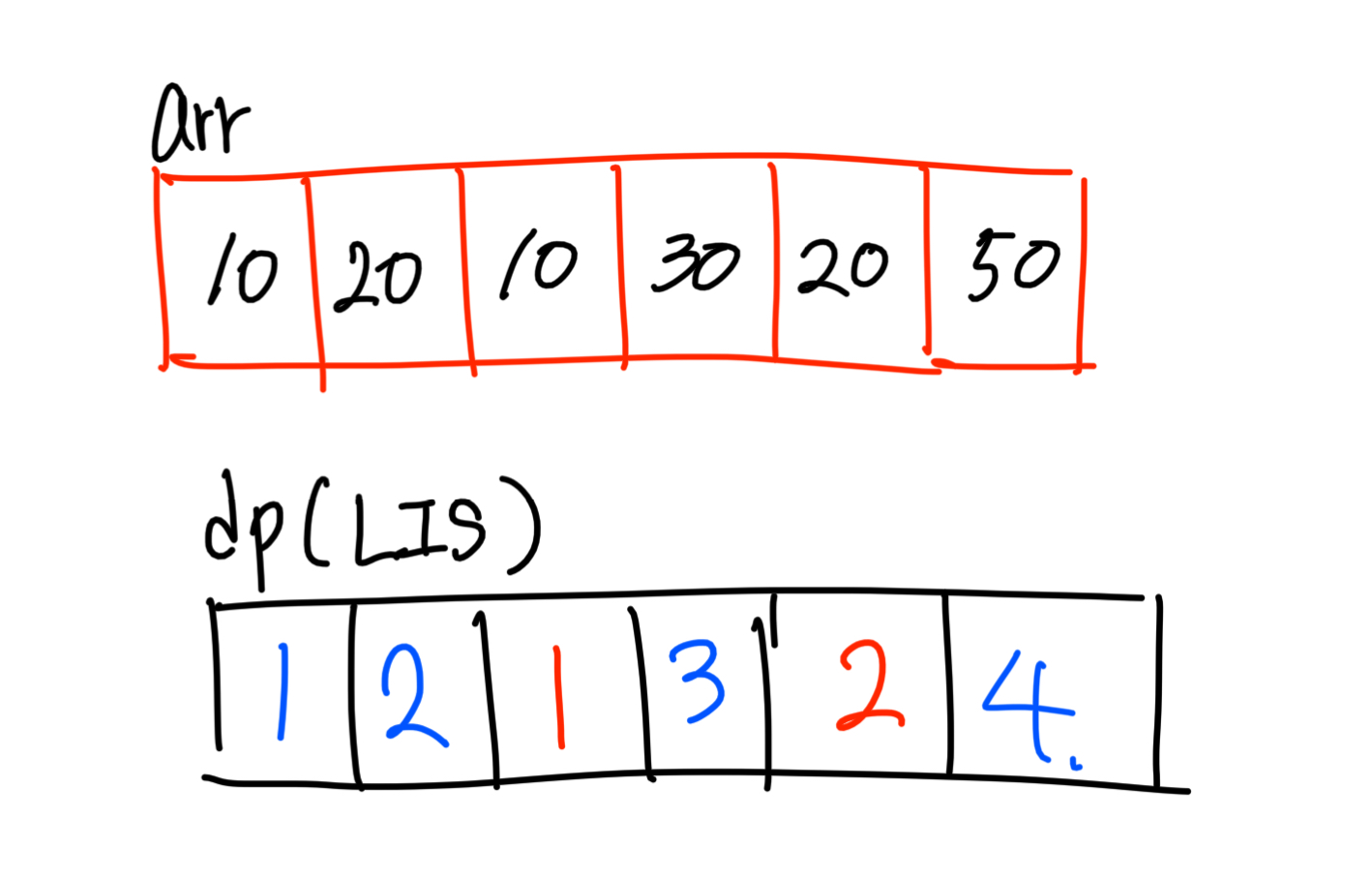
1. 이미지에 있는 arr배열의 LIS를 구할 것이고 그 값을 dp배열에 저장할 것이다.

2. 첫번째 값의 경우 이전에 값이 없으므로 LIS는 1이다.
   
   

3. 두번째 원소 20의 경우 두가지 경우의 수가 있다. 20에서 다시 시작하는 경우와 이전에 작은 값이 있다면 이어서 가는 경우가 있다. 이전에 작은 값인 10이 있으므로 1이 아닌 2가 된다.

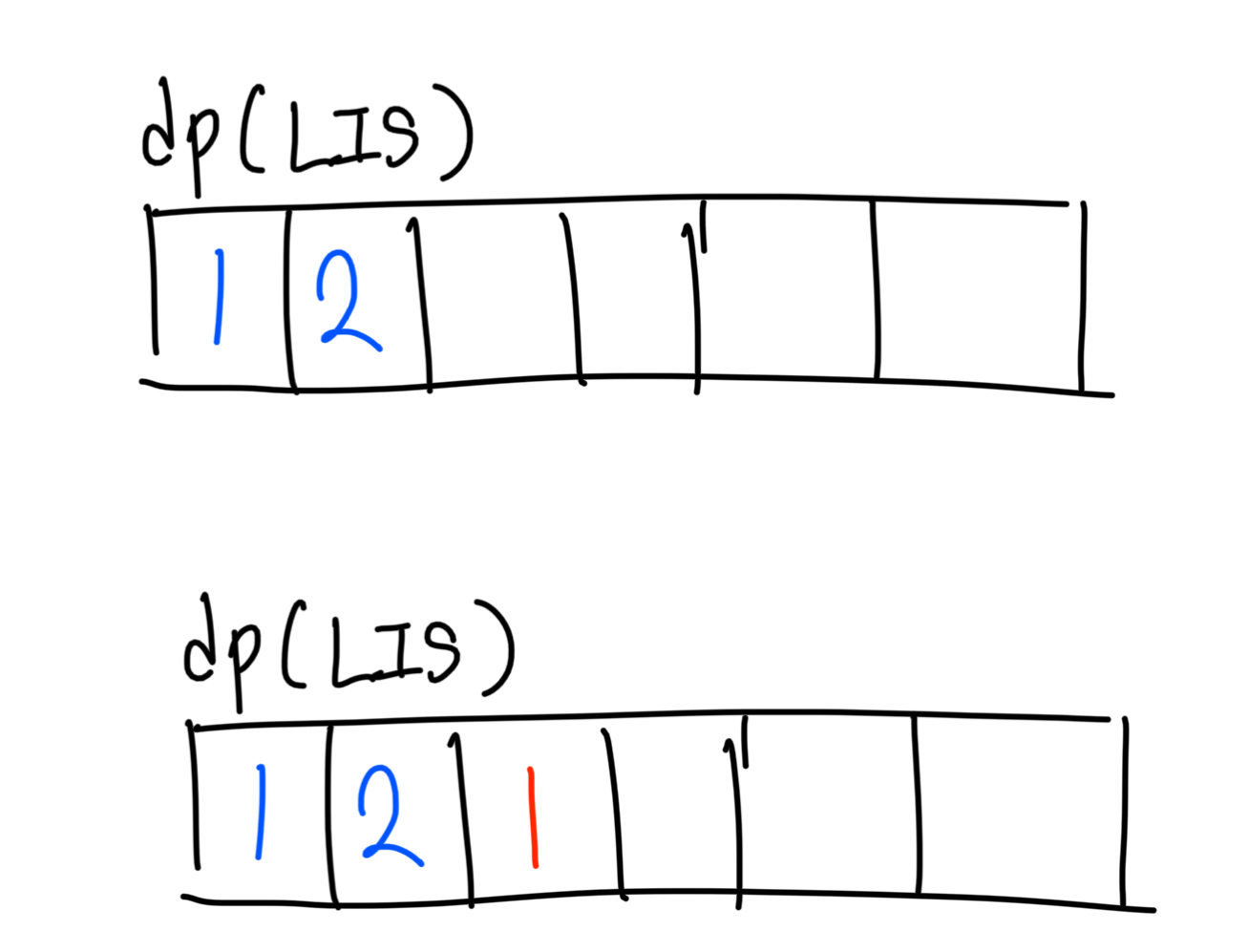
4. 세번째 원소 10은 이전에 10보다 작은 값이 없으므로 LIS는 1이 된다.
   
   

5. 네번째 원소는 30이다. 30의 경우 직관적으로 보면 10,20에 이어 30이 되는 경우가 가장 LIS가 큰 경우임을 확인할 수 있다.

   이를 통해 규칙성을 파악하면 해당 원소의 이전 인덱스들을 탐색하면서 작은 값을 찾고 작은 값들 중 dp배열의 값이 가장 큰 값을 찾아 +1하면 해당 원소의 LIS가 된다

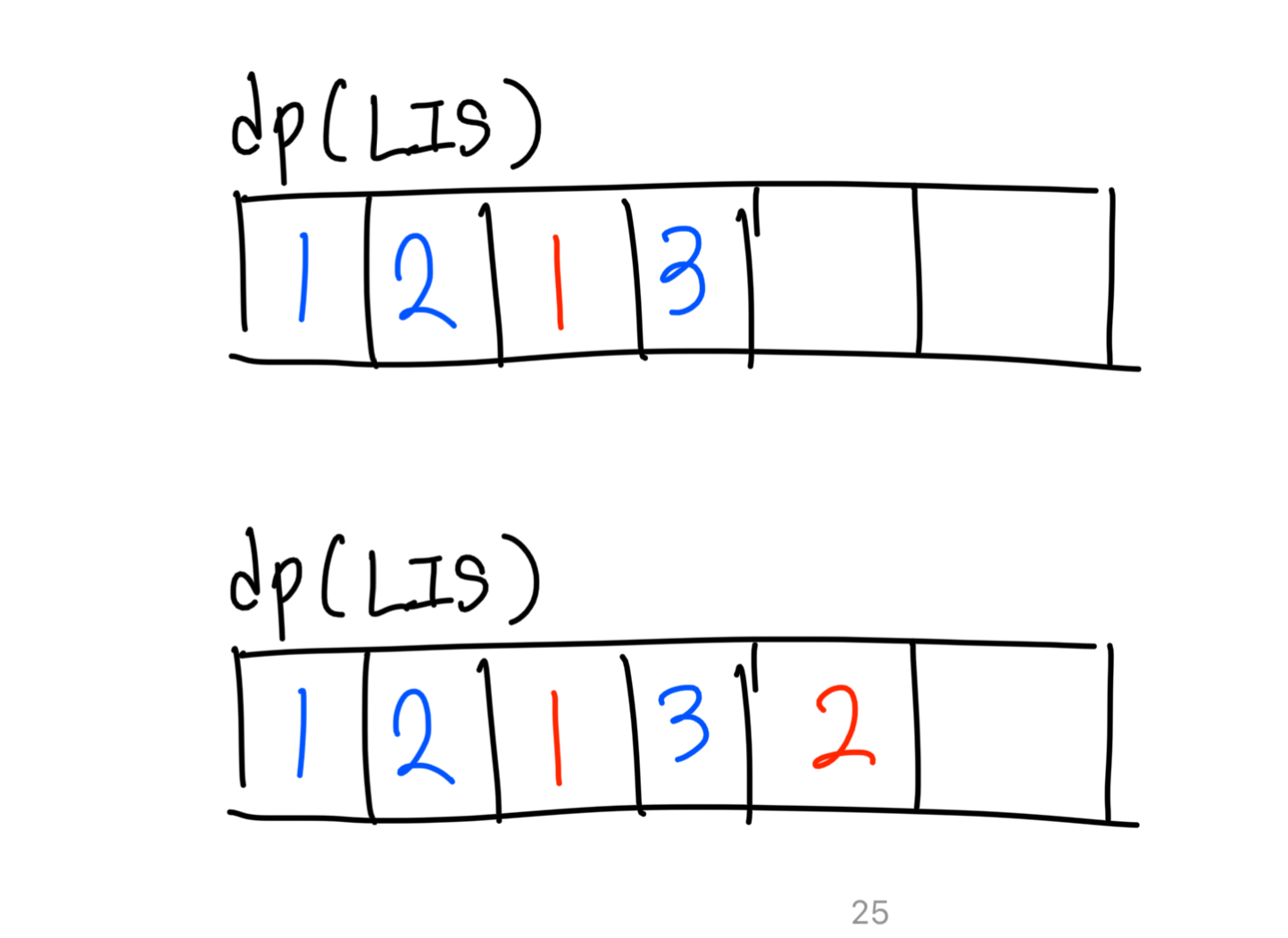
6. 다섯번째 원소는 20이다. 20보다 원소가 작은 인덱스는 첫번째 인덱스와 세번째 인덱스가 있다.(값 = 10)
   즉, 다섯번째 원소가 가질 수 있는 LIS 값은 [10] - [20] 이므로 2이다.
   
   

7. 마지막 원소의 값은 50이다. 이전의 모든 인덱스들이 해당 원소보다 값이 작으므로
   이전의 LIS중 가장 큰값 +1이 마지막 원소의 LIS값이다. 즉 LIS는 4가 된다.
   

이를 코드로 표현한다 생각해보자

조건 1. dp[i] = 1 로 매번 초기화
조건 2. i번째 원소의 이전 값들을 조회해 i번째 값보다 작으면 dp[i]보다 큰 dp[j]+1을 찾는다.
dp[i] = Math.max(dp[i],dp[j]+1)

구현 - 동적계획법

int [] arr = {10,20,10,30,20,50);
int [] dp = new int[6];
int max = 0;

for(int i = 0; i<arr.length; i++) {
	int dp[i] = 1;	
    for(int j = 0; j<i; j++) {
    	//j번째 원소가 i번째 원소보다 작으면 갱신
    	if(arr[j]<arr[i]) {
        	dp[i] = Math.max(dp[i],dp[j]+1);
     	}
     }
     //전체 수열의 LIS 최대 값을 구한다.
     max = Math.max(max,dp[i]);
 }
 
 System.out.println(max);