정렬(Sort)

1. 선택 정렬(selection-sort)

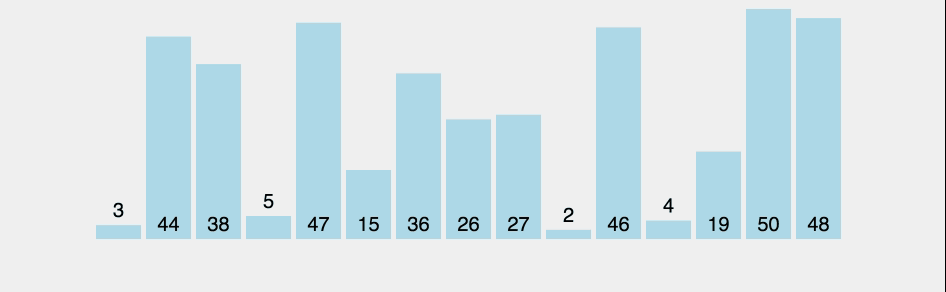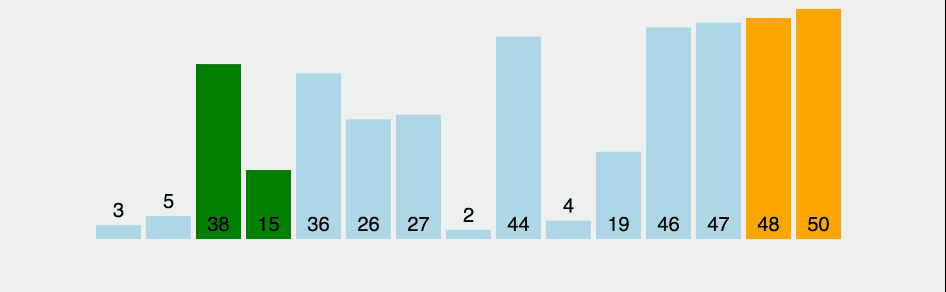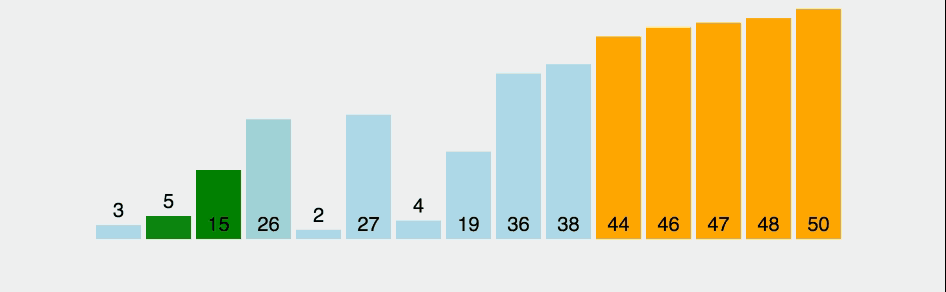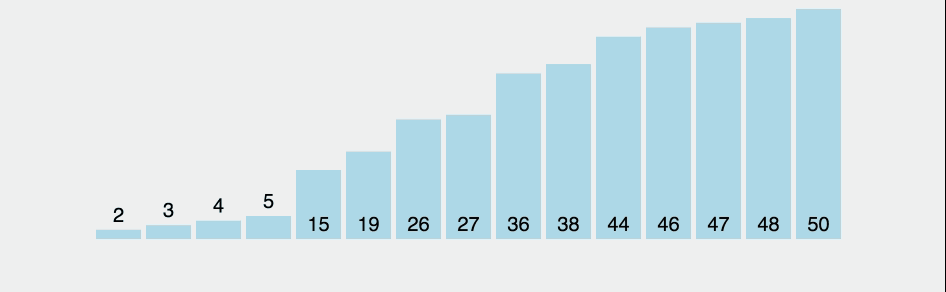
선택 정렬(selection-sort)이란?

잘못된 위치에 들어가 있는 원소를 찾아 올바른 위치에 교환하여 집어넣는 방법.

시간복잡도: O(n^2)
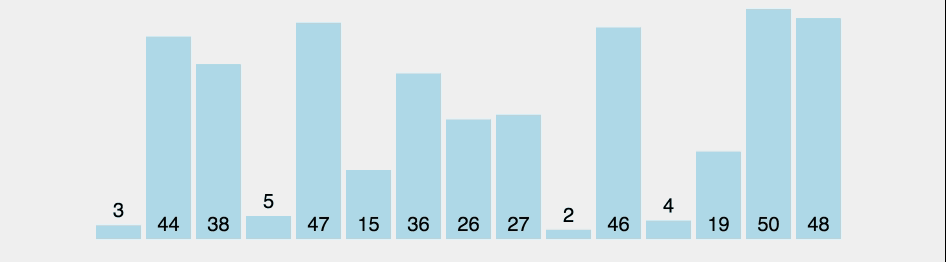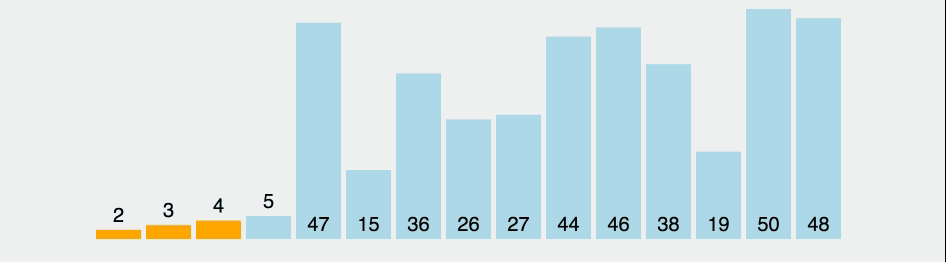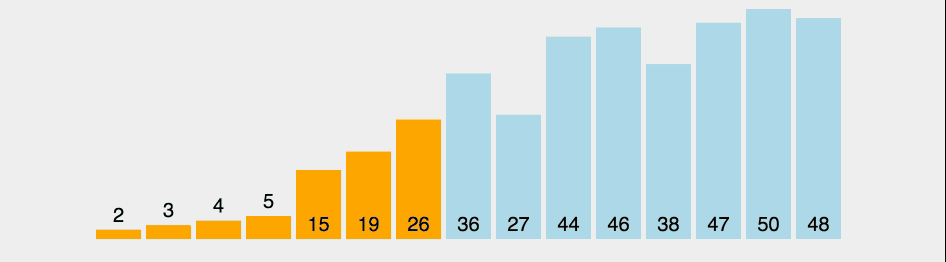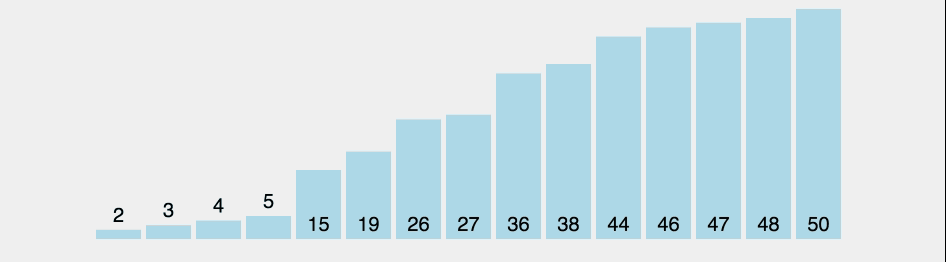이미지 출처

selectionSort(a[]) {
min = a[0]; //최솟값을 초기화.
		loc = 0; //최솟값을 놓을 위치 변수
		minLoc = 0; //최솟값이 있는 위치 변수
		
		//배열 안에서 최솟값 찾기
		for(int i = 0; i < a.length(); i++) {
			if(min > a[i]) {
				min = a[i];
				minLoc = i;
			}
				
		}
		
		//교환하기
		tmp = a[loc]; //임시 저장소
		a[loc] = min;
		a[minLoc] = tmp;
}

2. 버블 정렬(bubble-sort)

버블 정렬(bubble-sort)이란?

배열을 검사하여 두 인접한 원소가 오름차순 정렬 순서에 맞지 않으면 이들을 서로 교환하는 방법.

시간복잡도: O(n^2)

이미지 출처

bubbleSort(a[]) {
	for(int i = a.length - 1; i >= 0 ; --i) {
		for(int j = 0; j < i; j++) {
			if(a[j] > a[j+1]) {
				//교환하기
				tmp = a[j]; //임시 저장소
				a[j] = a[j+1];
				a[j+1] = tmp;
			}
		}
}

3. 삽입 정렬(insertion-sort)

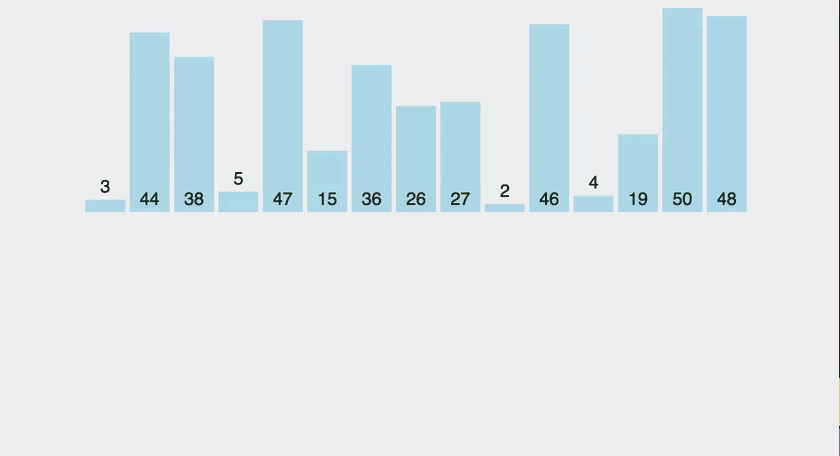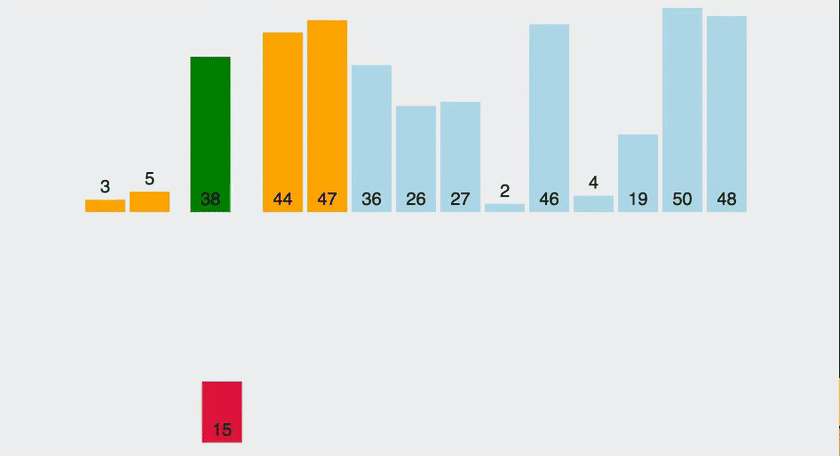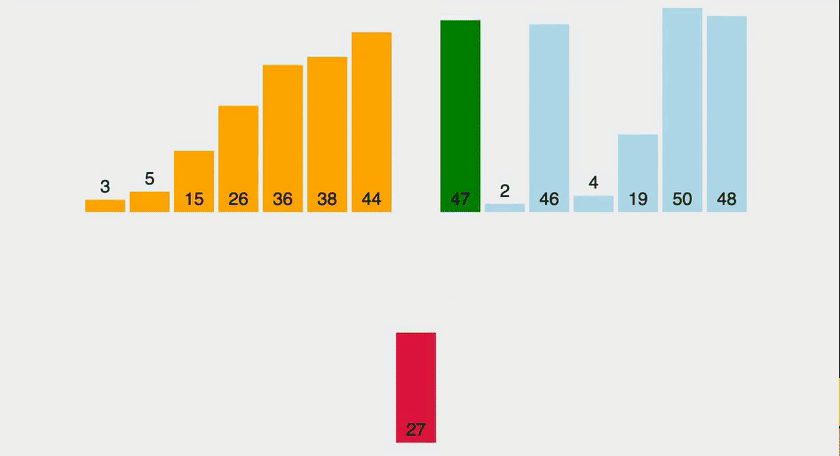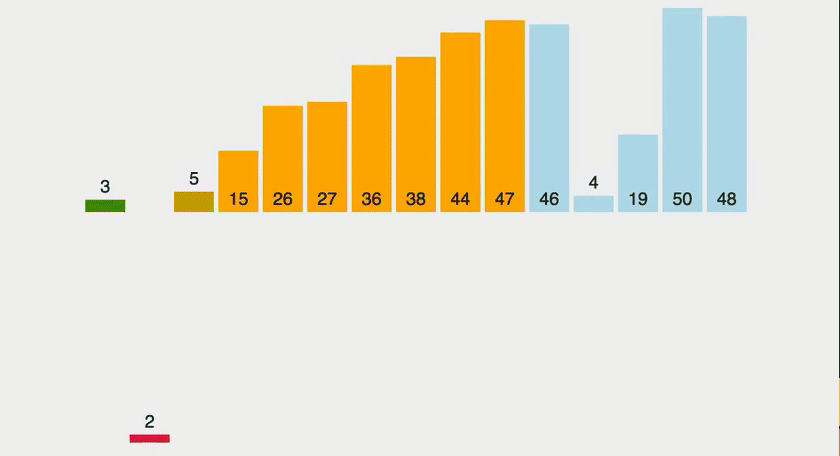
삽입 정렬(insertion-sort)이란?

정렬해야 될 배열을 그대로 사용하면서 배열 속에 있는 모든 원소를 정렬하는 방법.

시간복잡도: O(n^2)
이미지 출처

insertionSort(a[]) {
			for (int i = 1; i < a.length(); i++) {
				temp = a[i]; //임시 저장소
				j = i;
				
				if(a[j-1] > temp)
					move = true; //move는 원소를 이동할지 판정하는 변수
				else 
					move = false;
				
				//값이 더 작은 원소를 넣기 위해 원소 이동
				while (move) {
					a[j] = a[j-1];
					j = j-1;
					
					//바꾼 위치의 원소도 조건에 해당하는지 확인하여 조건을 충족하면 반복, 아니면 반복문 종료
					if(j>0 && a[j-1] > temp)
						move = true;
					else
						move = false;			
					
				}
						
			}
		}		

4. 합병 정렬(merge-sort)

합병 정렬(merge-sort)이란?

1) 배열 A를 배열 L, R로 이등분하기
2) 배열 L, R을 각각 정렬하기
3) L, R을 합병하기

시간복잡도: O(nlogn)
이미지 출처

mergeSort(a[]) {
			if(a.length() > 1) {
				middle = (0 + a.length()) / 2; //배열 a의 중앙값 위치 변수
				
				//배열 a를 배열 L, R로 나누기
				L[] = a[0:middle];
				R[] = a[middle+1: a.length()];
				
				//순환적으로 배열 L, R을 정렬하기
				mergeSort(L[]);
				mergeSort(R[]);
				
				//정렬이 끝난 배열 L, R을 다시 합병치기
				merge(L[], R[]);
			}			
			
		}

5. 퀵 정렬(quick-sort)

퀵 정렬(quick-sort)이란?

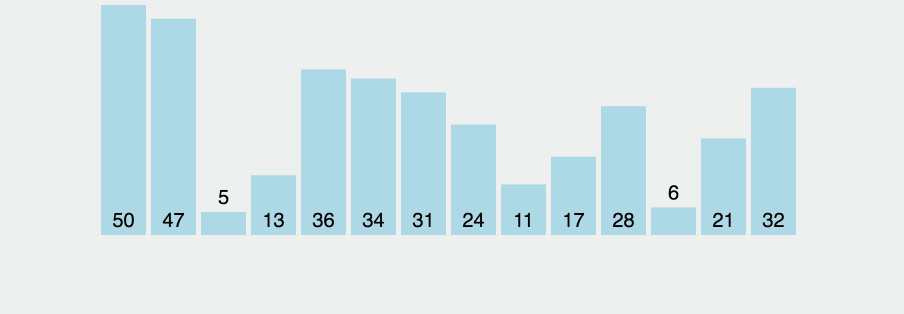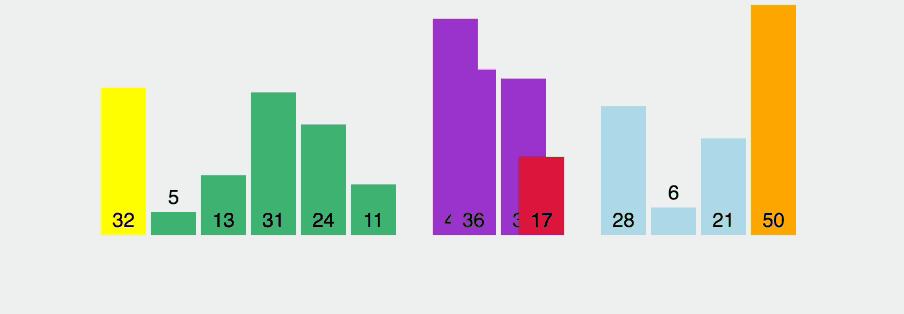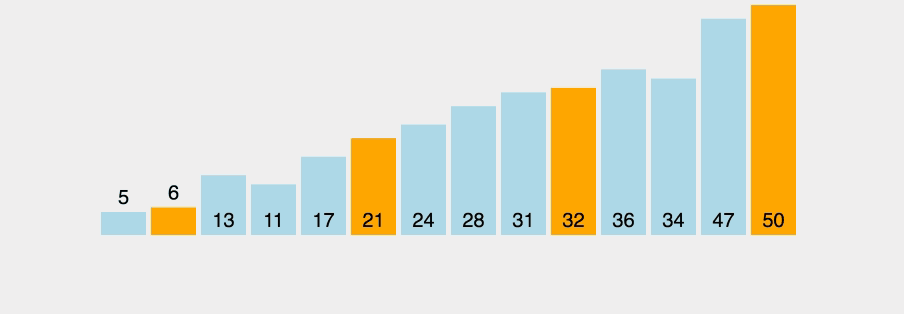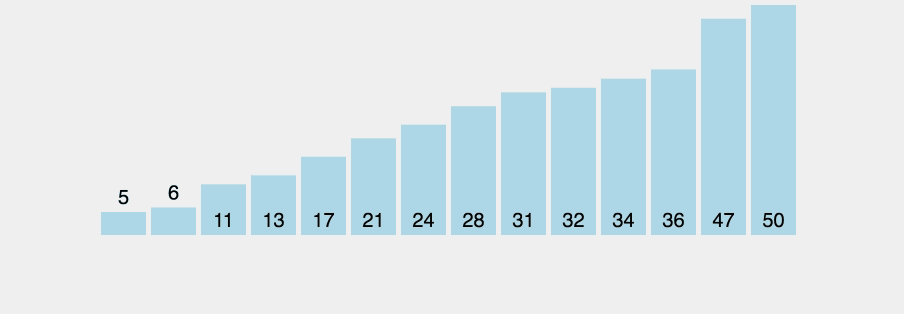
1) 배열 a의 원소 하나를 피봇(pivot)으로 선정
2) 피봇을 기준으로 2개의 파티션(partition)으로 분할

• 왼쪽 파티션은 피봇보다 작은 값의 원소들로 구성
  오른쪽 파티션은 피봇보다 큰 값의 원소들로 구성

시간복잡도: O(nlogn)
이미지 출처

quickSort(a[]) {
			//배열 a를 오름차순으로 정렬
			//정렬할 원소의 개수가 1개보다 많아야 함
			if (!(0 >= a.length()) {
				pivot = partition(a[]); //피봇의 위치를 알려주는 변수
				
				//순환적으로 왼쪽 파티션과 오른쪽 파티션을 정렬
				quickSort(a[0:p-1]);
				quickSort(a[p+1:a.length()]);
			}
		}

6. 히프 정렬(heap-sort)

히프 정렬(heap-sort)이란?

1) 정렬할 원소를 모두 공백 히프에 넣기
2) 히프의 원소를 하나씩 삭제한 후, 배열 뒤에 차례대로 삽입

시간복잡도: O(nlogn)
이미지 출처

heapSort(a[]) {
			size = a.length() - 1; //히프의 실제 크기
		
			//배열 a를 히프로 변환
			for(int i = size / 2; i >= 2; i = i-1) {
				heapify(a[], i, size); 
			}
			
			//히프에서 삭제 연산을 하면서 배열 a를 정렬
			for (int  i = size; i >=2; i = i-1) {
				heapify(a[], 1, i - 1);
				temp = a[1];
				a[1] = a[i];
				a[i] = temp;
			}
		}

참고자료: 자료 구조와 JAVA(이석호 저, 정익사, 2004)