[자료구조] 트리

Woonil·2025년 2월 18일

자료구조

목록 보기

1/1

트리란 자료들이 계층관계로 이루어진 비선형 자료구조를 말한다.

정의 = 무방향이면서 사이클이 없는 연결 그래프 = 연결 그래프이면서, 임의의 간선을 제거하면 연결 그래프가 아니게 되는 그래프 = 임의의 두 점을 연결하는 단순 경로가 유일한 그래프 = V개의 정점을 가지고, V-1개의 간선을 가지는 연결 그래프 = 사이클이 없는 연결 그래프이면서 임의의 간선을 추가하면 사이클이 생기는 그래프 = V개의 정점을 가지고 V-1개의 간선을 가지는 사이클이 없는 그래프

구성

노드: 트리를 구성하는 원소(자료)

명칭	설명
루트(Root) 노드	트리의 시작 노드 (레벨 0의 노드)
형제(Sibling) 노드	같은 부모 노드를 가진 자식 노드들
조상(Ancestor) 노드	한 노드에서 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드
리프(Leaf) 노드 (단말 노드)	자식 노드가 없는 노드 (차수가 0인 노드)
내부(Internal) 노드	차수가 1 이상인 노드

간선: 노드를 연결하는 선
높이: 한 노드의 높이는 그 노드에 이르는 경로에 있는 간선의 수
서브트리 (subtree): 어떤 한 정점에 대해 그 밑에 있는 정점과 간선만을 모은 트리
차수 (degree): 한 노드가 가지는 서브 트리의 수 (자식 노드의 수) cf) 트리의 차수는 노드의 차수 중에서 가장 큰 값이다.

🤔개념

이진 트리

이진 트리(Binary Tree)는 트리의 모든 노드의 차수를 2 이하로 제한하여 전체 트리의 차수가 2 이하가 되도록 정의한 트리이다.

특징
- 노드가 n개일 경우, 간선은 항상 (n-1)개이다.
- 높이가 h인 이진 트리가 가질 수 있는 노드 개수
  - h=0부터 시작 ⇒ 최소: (h+1)개, 최대: 2^(h+1)-1 (첫항이 1이고 항의 개수가 h+1인 공비 2인 등비수열의 합)개
  - h=1부터 시작 ⇒ 최소: h개, 최대: 2^h-1개
- 레벨 i에서 최대 노드 수
  - h=0부터 시작 ⇒ 2^(h-1)
  - h=1부터 시작 ⇒ 2^h

종류

완전 이진 트리(Complete Binary Tree)
높이가 h이고, 노드 수가 n (n<2^(h+1)-1)개일 때, 노드 위치가 포화 이진 트리에서의 노드 1번부터 n번까지의 위치와 완전히 일치하는 이진 트리

Full Binary Tree

자식노드 수가 0이거나 2인 완전 이진 트리
- 특징
  - 트리높이 : log2(n+1) 올림
  - 마지막 노드 수 X 2 : 2^k - 1 - (2^(k-1)-1) = 1/2(n+1) → X2
- 포화 이진 트리(Perfect Binary Tree)
  모든 레벨에 노드가 꽉 차 높이를 늘이지 않는 한 노드를 추가할 수 없는 포화 상태의 이진 트리로, 완전 이진 트리에 속한다.

구현

배열을 이용한 구현
높이가 h인 포화 이진 트리의 노드 번호를 배열의 인덱스로 사용하여 1차원 배열로 표현 1차원 배열에서 인덱스 계산을 쉽게 하기 위해 인덱스 0번은 실제로 사용하지 않고 비워 두고 항상 인덱스 1번부터 노드를 저장
- 노드 인덱스
  - └ i/2 ┘: 노드 i의 부모노드의 인덱스
  - i*2: 왼쪽 자식노드의 인덱스
  - (i*2+1): 오른쪽 자식노드의 인덱스

연결리스트를 이용한 구현

typedef struct treeNode {
	char data;
	struct treeNode *left;
	struct treeNode *right;
} treeNode;

순회

[사진 자료 출처]

[자료구조 알고리즘] Binary Tree의 3가지 순회방법 구현하기

전위 순회 (preorder)

현재노드 방문(D) → 왼쪽 서브트리 이동(L) → 오른쪽 서브트리 이동(R)
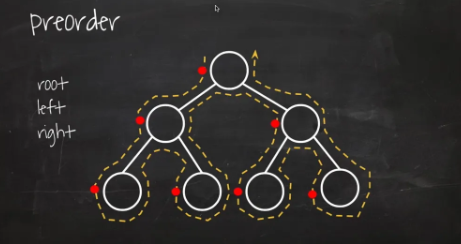
중위 순회 (inorder)

왼쪽 서브트리 이동(L) → 현재노드 방문(D) → 오른쪽 서브트리 이동(R)
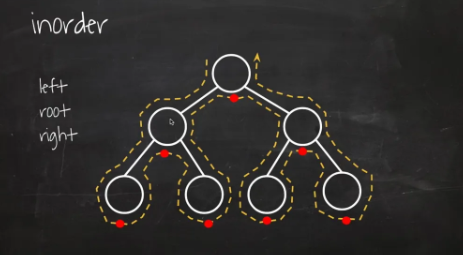
후위 순회 (postorder)

왼쪽 서브트리 이동(L) → 오른쪽 서브트리 이동(R) → 현재노드 방문(D)
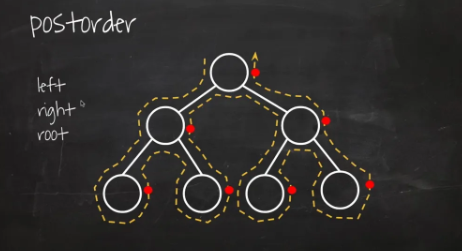
순회 결과로 원본트리 재현
- 전위 + 중위
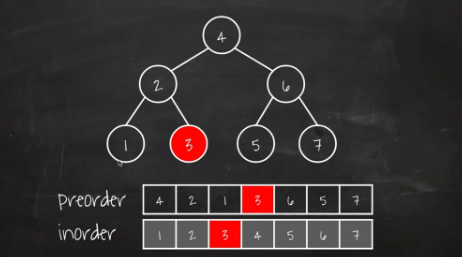
```
		1) 전위 순회 ⇒ 루트노드의 정보, 루트의 왼쪽 서브트리의 루트 정보

		2) 중위 순회 ⇒ 전위 순회로부터 얻은 루트노드, 서브트리의 루트로부터 각 루트의 왼쪽, 오른쪽 서브트리를 구분
```
- 중위 + 후위
```
 
```
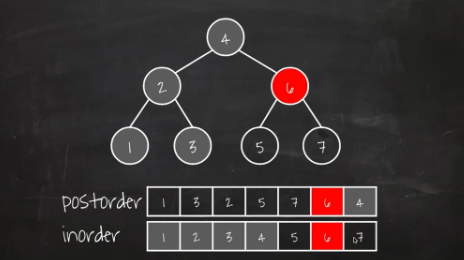
- 전위 + 후위
  
  Full Binary Tree 일때만 가능
  
  cf) Full Binary Tree는 자식노드가 아예 없거나 둘만 있는 이진트리를 의미한다. Perfect Binary Tree (포화이진트리) 가 아님에 유의

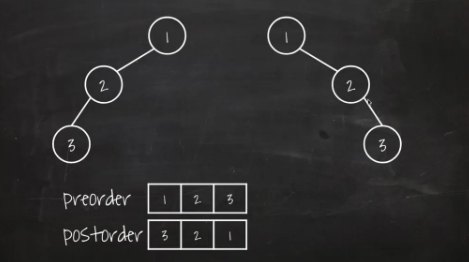
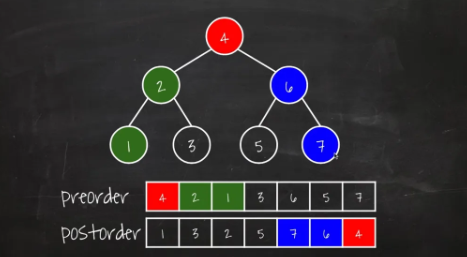
이진 검색 트리 (Binary Search Tree)

탐색을 위해 저장할 데이터의 크기에 따라 노드 위치를 정하도록 정의된 이진 트리로, 왼쪽 서브트리의 모든 값은 부모의 값보다 작고, 오른쪽 서브트리의 모든 값은 부모의 값보다 크다.

조건
- 모든 원소는 서로 다른 유일한 키를 가진다.
- 왼쪽 서브 트리에 있는 원소들의 키는 그 루트의 키보다 작다.
- 오른쪽 서브 트리에 있는 원소들의 키는 그 루트의 키보다 크다.
- 왼쪽 서브 트리, 오른쪽 서브 트리 모두 이진 탐색 트리이다.
특징
- 원소가 크기 순으로 정렬되어 있다. ⇒ CRUD가 빈번하고, 원소의 대소와 관련된 성질에 관한 문제에서 유용하다.

[바킹독의 실전 알고리즘] 0x16강 - 이진 검색 트리

최적 이원 탐색 트리(Optimal Binary Search Tree)

효율적인 이진탐색트리

Static Optimality Problem: ‘이미 정해진 노드로 어떻게 이진탐색트리를 구성해야 효율적인가’에 관한 문제

Dynamic Optimality Problem: ‘노드 추가 및 삭제시 어떻게 이진탐색트리를 구성해야 효율적인가’에 관한 문제

정렬된 배열을 BST로 변환

// 노드 구조체 정의 
struct TreeNode {
		int val;
    struct TreeNode *left;
    struct TreeNode *right;
};
 
// 새로운 노드를 반환하는 함수 정의
struct TreeNode* newNode(int val){
    struct TreeNode* new = malloc(sizeof(struct TreeNode));
    new->val = val;
    new->left = NULL;
    new->right = NULL;
    return new;
}

// 배열을 BST로 변환하는 함수
struct TreeNode* ArrayToBST(int* nums, int start, int end){
    if(start>end)
        return NULL;
    
    int mid = (start+end)/2;
    struct TreeNode* root = newNode(nums[mid]);
    
    root->left = ArrayToBST(nums,start,mid-1);
    
    root->right = ArrayToBST(nums,mid+1,end);
    
    return root;
}

struct TreeNode* sortedArrayToBST(int* nums, int numsSize){
    return ArrayToBST(nums, 0, numsSize-1);
}

정렬된 연결리스트를 BST로 변환

// 연결리스트 정의
struct ListNode {
     int val;
     struct ListNode *next;
}; 
// 노드 구조체 정의 
struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
};
 

struct TreeNode* buildBST(struct ListNode* head, struct ListNode* tail) {
    if (head==tail)
        return NULL;
    struct ListNode* fast = head;
    struct ListNode* slow = head;
		// 런너 기법을 활용
    while (fast != tail && fast->next != tail) {
        fast = fast->next->next;
        slow = slow->next;
    }
    struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    node->val = slow->val;
    node->left = buildBST(head, slow);
    node->right = buildBST(slow->next, tail);
    return node;
}

struct TreeNode* sortedListToBST(struct ListNode* head){
    if (!head) 
        return NULL;
    else
        return buildBST(head, NULL);
}

히프 (Heap)

완전 이진 트리에 있는 노드 중에서 키값이 가장 큰 노드나 키값이 가장 작은 노드를 찾기 위해 만든 자료구조

특징
- 같은 키값의 노드가 중복되어 있을 수 있다.
- 우선순위 큐를 구현하기 위하여 사용하는 자료구조 중 하나이다.
조건
- 완전 이진 트리여야 한다.
- 힙 속성을 만족해야 한다.
  - 각 노드의 값이 자식 노드보다 크거나 같다(작거나 같다).
  - 최댓값 또는 최솟값은 최상단인 루트 노드에 위치한다.

구현

생성과 삽입 및 삭제

#pragma once
#define MAX_ELEMENT 100

#include <stdio.h>
#include <stdlib.h>
#include "heap.h"

// 히프에 대한 1차원 배열과 히프 원소의 개수를 구조체로 묶어서 선언
typedef struct {
  int heap[MAX_ELEMENT];
  int heap_size;
} heapType;

heapType* createHeap(void);
void insertHeap(heapType* h, int item);
int deleteHeap(heapType* h);
void printHeap(heapType* h);

heapType* createHeap(void) {
  heapType* h = (heapType*)malloc(sizeof(heapType));
  h->heap_size = 0;
  return h;
}

  // 히프에 item을 삽입하는 연산
  void insertHeap(heapType* h, int item) {
    int i;
    h->heap_size = h->heap_size + 1;
    i = h->heap_size;
    while ((i != 1) && (item > h->heap[i/2])) {
      h->heap[i] = h->heap[i/2];
      i /= 2;
    }
    h->heap[i] = item;
  }

  // 히프의 루트를 삭제하여 반환하는 연산
  int deleteHeap(heapType* h) {
    int parent, child;
    int item, temp;
    item = h->heap[1];
    temp = h->heap[h->heap_size];
    h->heap_size = h->heap_size - 1;
    parent = 1;
    child = 2;
    while (child <= h->heap_size) {
      if ((child < h->heap_size) && (h->heap[child]) < h->heap[child + 1])
        child++;
      if (temp >= h->heap[child]) break;
      else {
        h->heap[parent] = h->heap[child];
        parent = child;
        child = child * 2;
      }
    }
    h->heap[parent] = temp;
    return item;
  }

💪실습

트리 모든 노드의 부모 찾기

import sys
sys.setrecursionlimit(10**6)
input=sys.stdin.readline

n=int(input())
graph=[[] for _ in range(n+1)]
p=[0]*(n+1)

def dfs(v):
    for i in graph[v]:
        # 방문했더니 나의 부모인 경우는 무시
        if p[v]==i:
            continue
        p[i]=v
        dfs(i)

for _ in range(n-1):
    u,v=map(int,input().rstrip().split())
    graph[u].append(v)
    graph[v].append(u)

dfs(1)
for i in range(2,n+1):
    print(p[i])

트리의 서브 트리의 정점 개수 찾기

import sys
sys.setrecursionlimit(10**6)
input=sys.stdin.readline

n,r,q=map(int,input().rstrip().split())
graph=[[] for _ in range(n+1)]
p=[0]*(n+1)
size=[0]*(n+1)

# dfs를 통해 정점의 부모들을 기록
def find_p(v):
    for i in graph[v]:
        if i==p[v]:
            continue
        p[i]=v
        find_p(i)

# 재귀를 통해 정점의 서브트리의 정점 개수 기록
def count_sub_tree_nodes(v):
    size[v]=1
    for i in graph[v]:
        if i==p[v]:
            continue
        count_sub_tree_nodes(i)
        # 자식 정점 방문 후의 결과를 현재 정점 size에 추가
        size[v]+=size[i]

for _ in range(n-1):
    u,v=map(int,input().rstrip().split())
    graph[u].append(v)
    graph[v].append(u)

find_p(r)
count_sub_tree_nodes(r)
for _ in range(q):
    print(size[int(input().rstrip())])

참고자료

[자료구조 알고리즘] Tree의 종류
[바킹독의 실전 알고리즘] 0x19강 - 트리

Woonil

프론트 개발과 클라우드 환경에 관심이 많습니다:)