들어가며
해당 강의를 보며 정리한 내용입니다.
이진 탐색 트리 (BST)
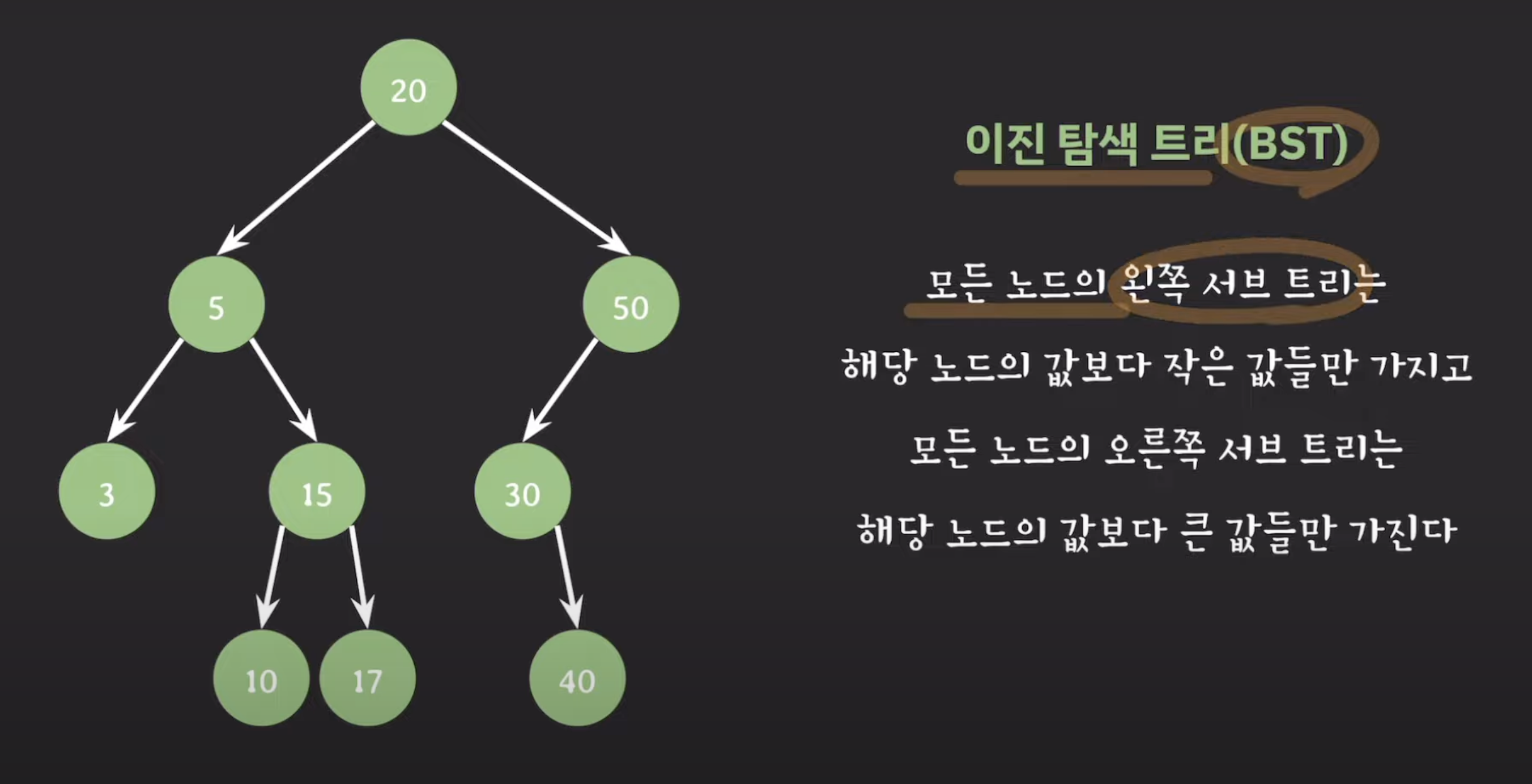
BST는 모든 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들만 가지고 있고, 모든 노드의 오른쪽 서브 트리는 해당 노드의 값보다 큰 값들만 가진다는 특징을 가집니다. 각 노드는 최대 두 개의 자식 노드를 가질 수 있습니다.
B-Tree
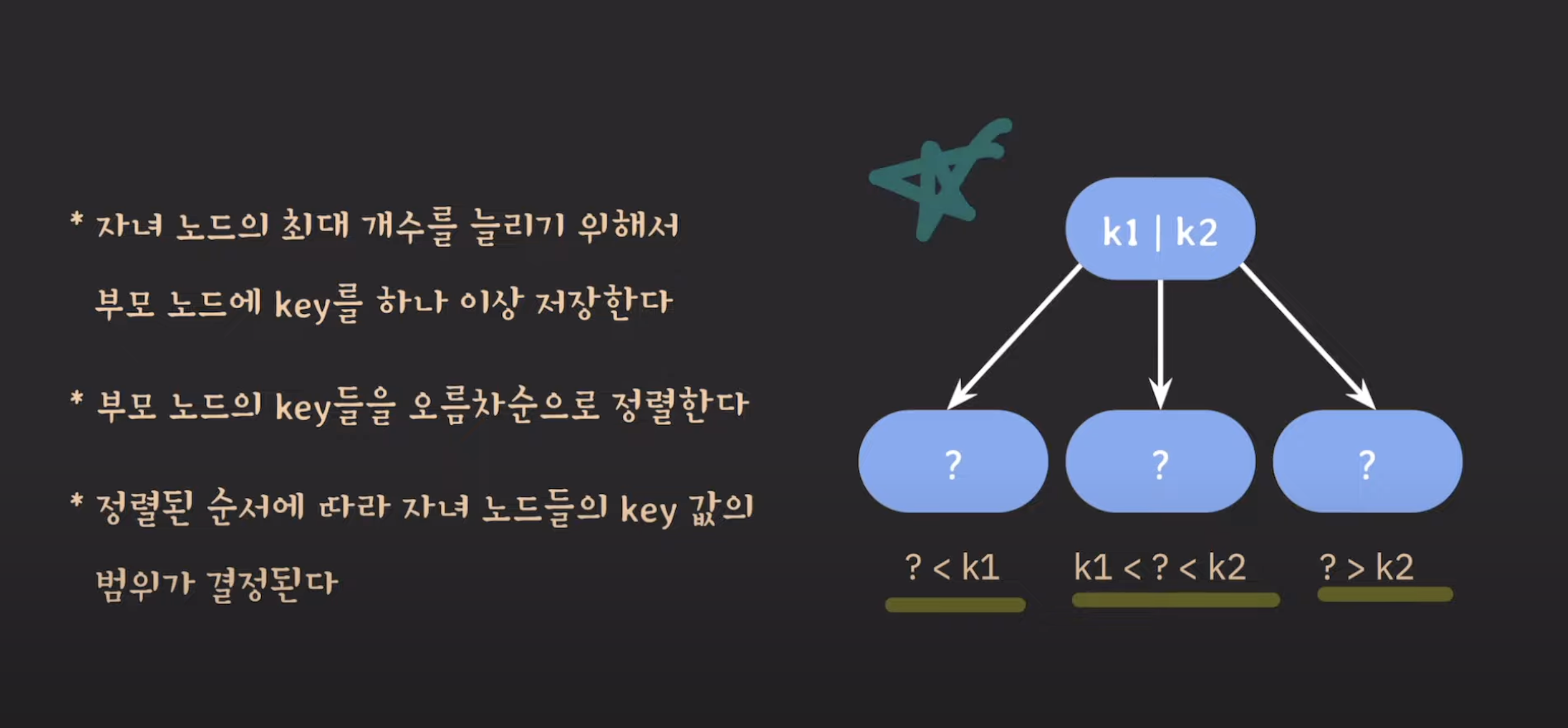
특징
B-Tree는 각 노드의 최대 자식 노드 수(M)를 늘리기 위해 부모 노드의 키를 하나 이상 저장합니다. 부모 노드의 키들은 오름차순으로 정렬되며, 정렬된 순서에 따라 자식 노드들의 키 값 범위가 결정됩니다. 이러한 방식을 사용하면 자식 노드의 최대 개수를 조절하여 사용자의 요구에 맞게 조정할 수 있습니다.
B-Tree의 주요 네 가지 파라미터
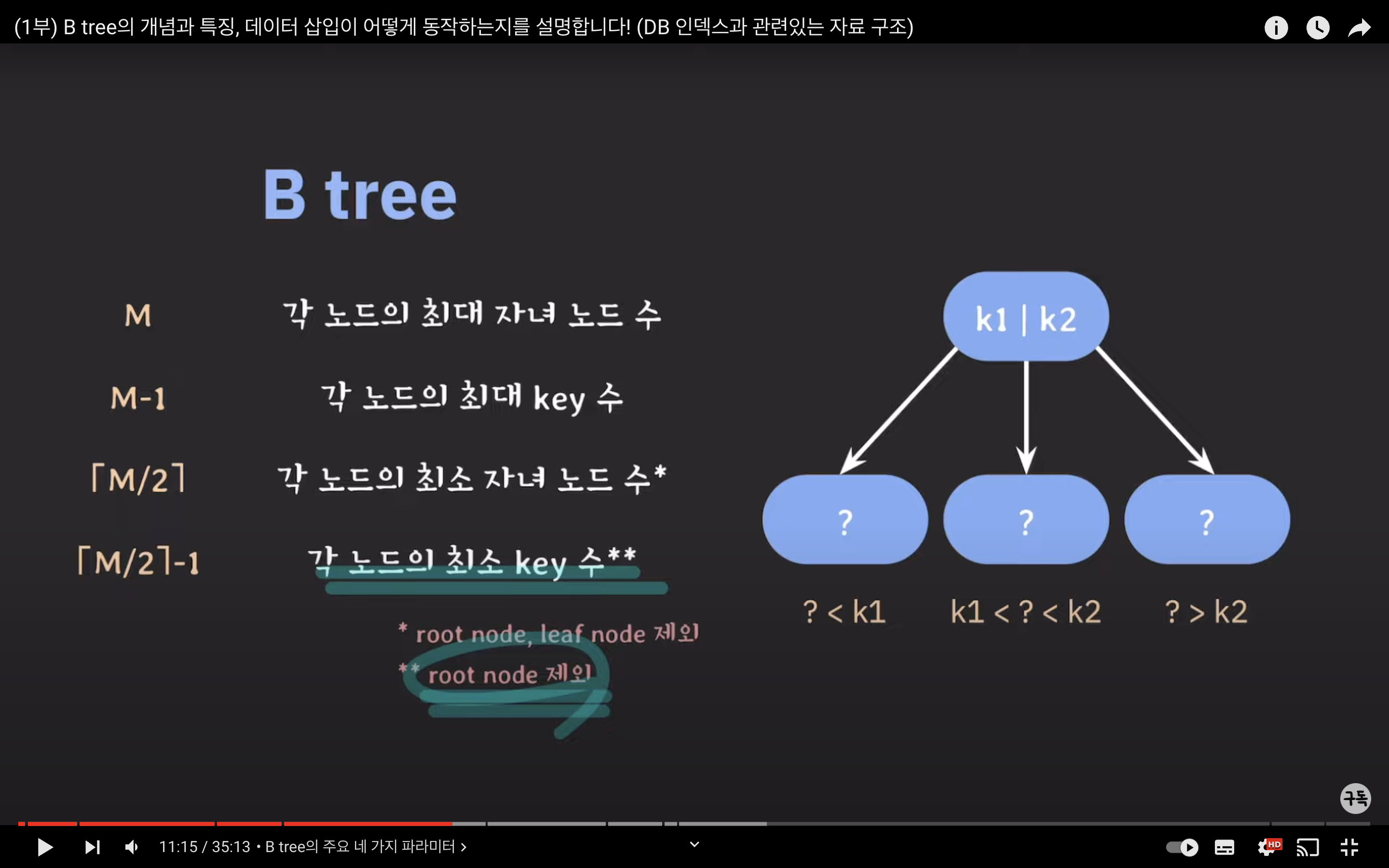
M
각 노드의 최대 자식 노드 수를 나타냅니다. 최대 M개의 자식을 가질 수 있는 B-Tree를 M차 B-Tree라고 부릅니다.
M - 1
각 노드의 최대 키(key) 수를 나타냅니다.
M / 2 (반올림)
각 노드의 최소 자식 노드 수를 나타냅니다. 이 값은 루트 노드와 잎 노드를 제외한 모든 내부 노드에 해당합니다.
(M / 2 (반올림)) -1
각 노드의 최소 키 수를 나타냅니다. 이 값은 루트 노드에 해당하지 않습니다.
B-Tree 노드의 key 수와 자녀 수의 관계
internal 노드의 key 수가 x개라면, 자녀 노드의 수는 언제나 x+1개다.
데이터 삽입
-
삽입 위치 찾기: 데이터를 삽입하기 위해 먼저 B-트리 내에서 데이터를 삽입할 위치를 찾아야 합니다. 이 위치는 leaf 노드 중 하나여야 합니다.
-
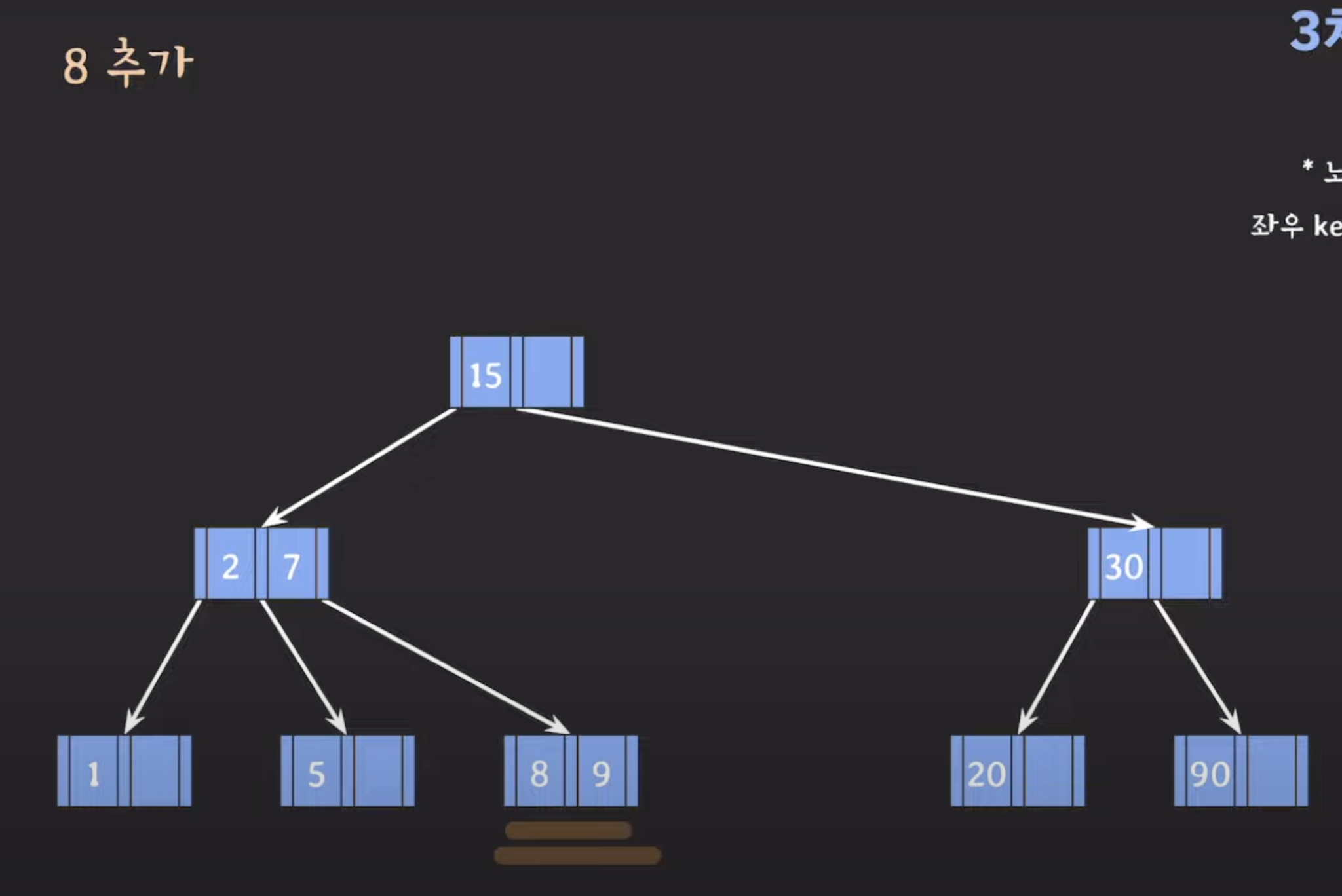
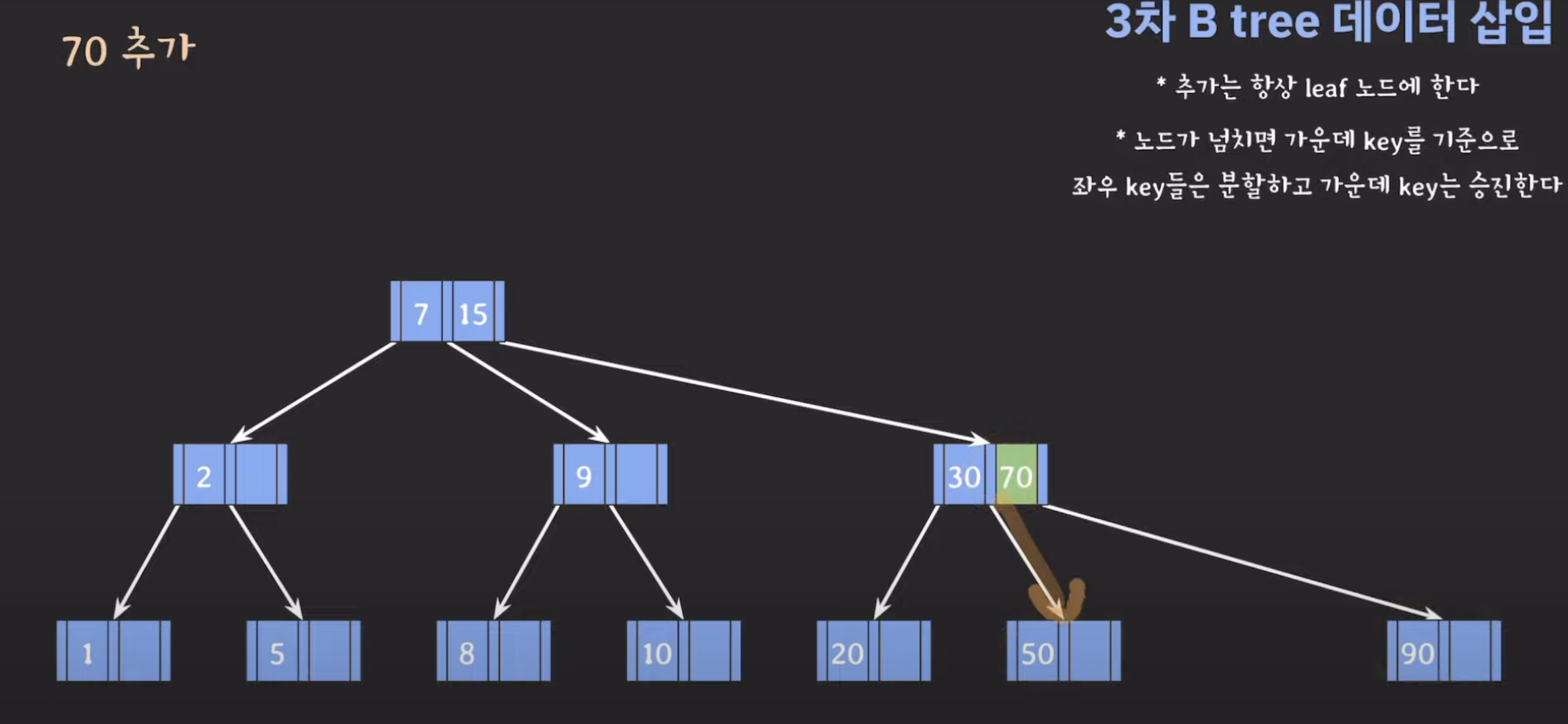
노드 넘침 확인: 데이터를 삽입하려는 leaf 노드가 이미 최대 키 수를 가진 경우, 노드가 넘치게 됩니다. 이때 분할 작업을 수행해야 합니다.
-
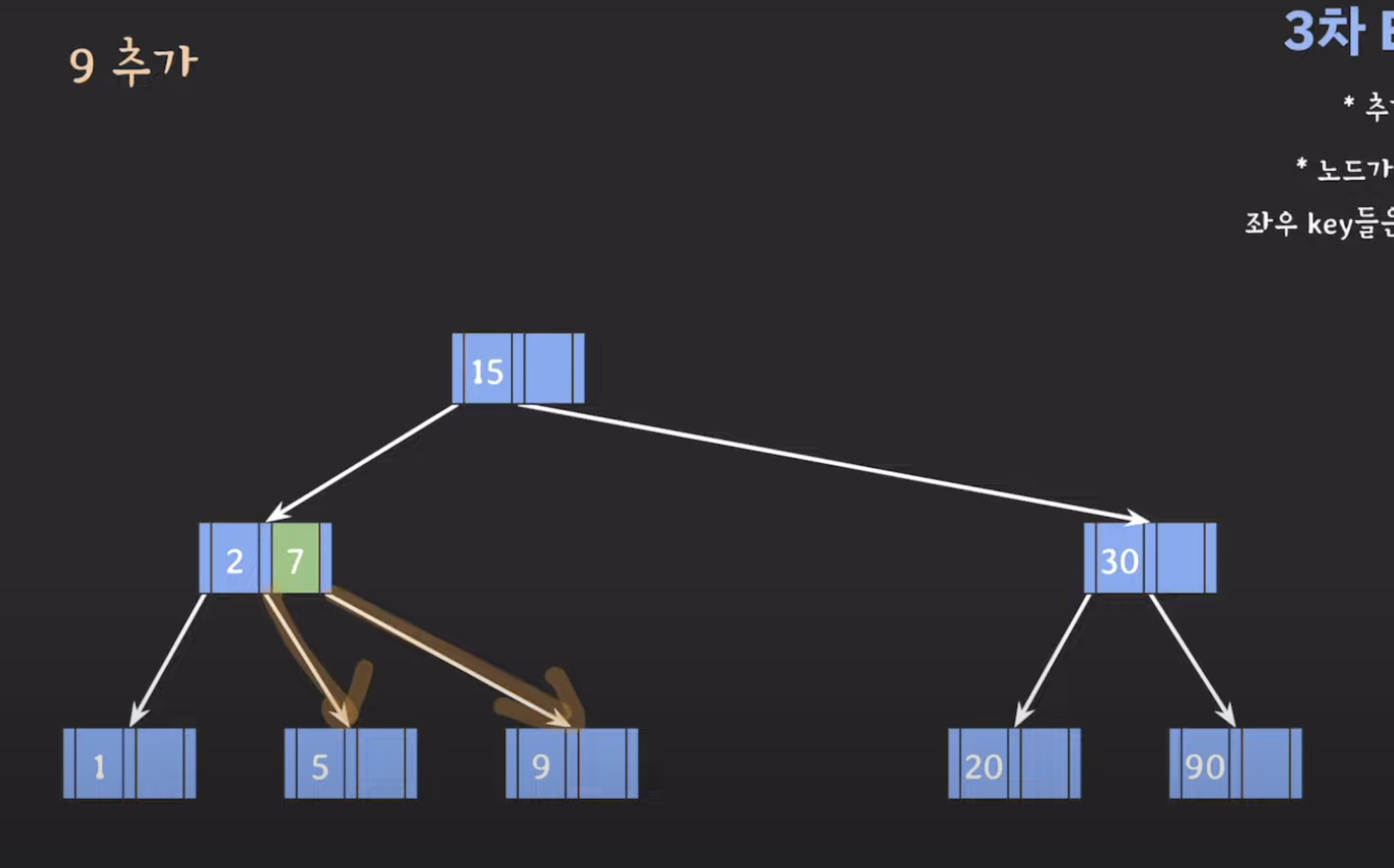
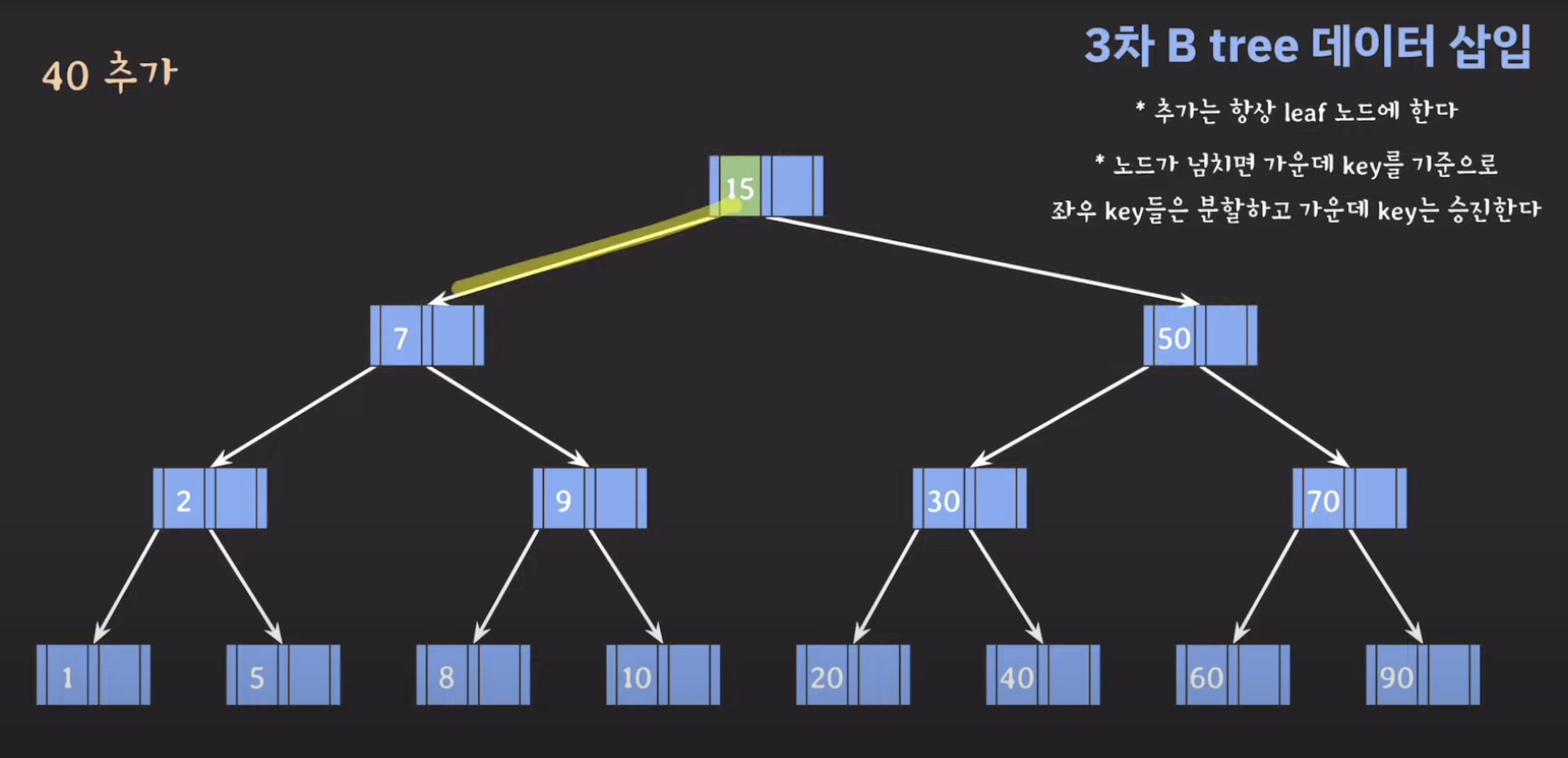
노드 분할: 넘치는 leaf 노드를 분할하고, 가운데(median) 키를 상위 레벨 노드로 승진시킵니다(오름차순으로 정렬됩니다). 분할 작업은 다음과 같이 수행됩니다:
-
넘친 노드의 키 중 중간 값(median key)을 찾습니다.
-
중간 값(median key)을 기준으로 작은 값들은 왼쪽 하위 노드로, 큰 값들은 오른쪽 하위 노드로 이동시킵니다.
-
중간 값(median key)은 상위 레벨 노드에 삽입됩니다. 만약 상위 레벨 노드도 넘치게 되면 재귀적으로 분할 작업을 수행합니다.
- 데이터 삽입: 삽입할 데이터를 적절한 leaf 노드로 삽입합니다. 만약 해당 노드가 넘친 경우, 분할 작업을 수행하고 중간 값은 상위 레벨 노드로 승진됩니다.
이런 방식으로 B-Tree는 항상 balanced tree를 유지하며 데이터를 삽입하고 검색할 수 있습니다. 이로써 B-트리는 조회 시 항상 일정한 시간 복잡도를 제공하며 데이터베이스와 파일 시스템에서 널리 사용됩니다.
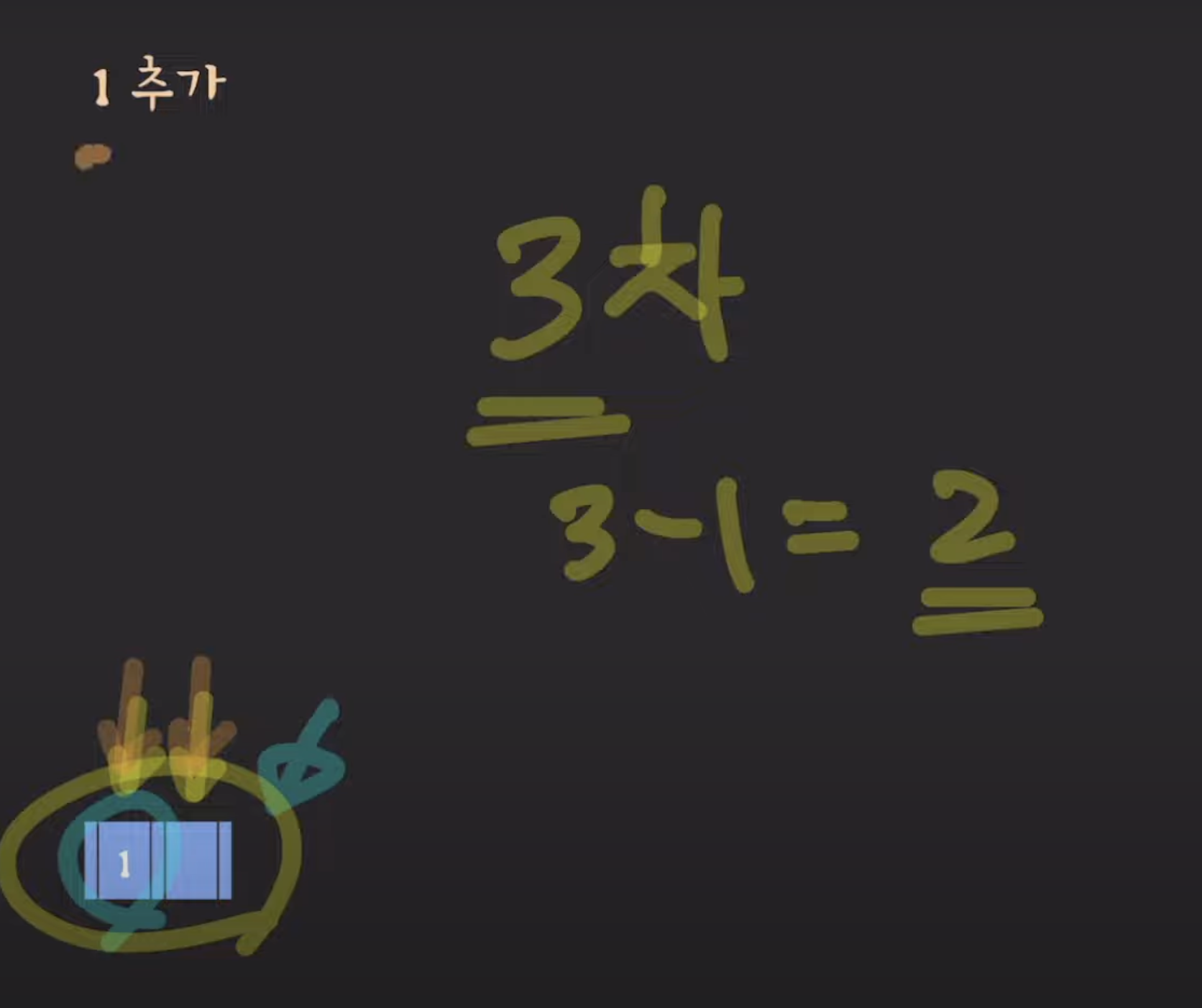
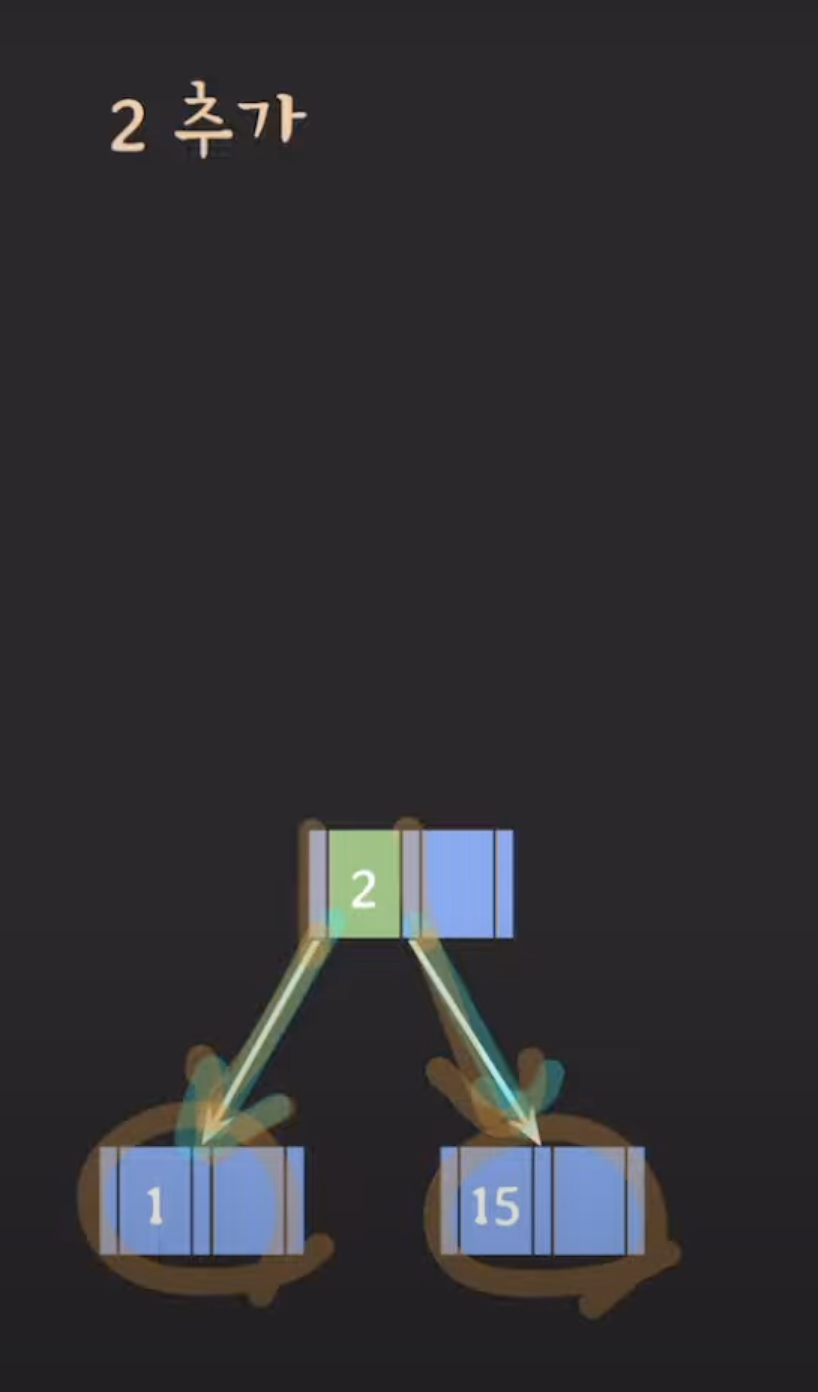
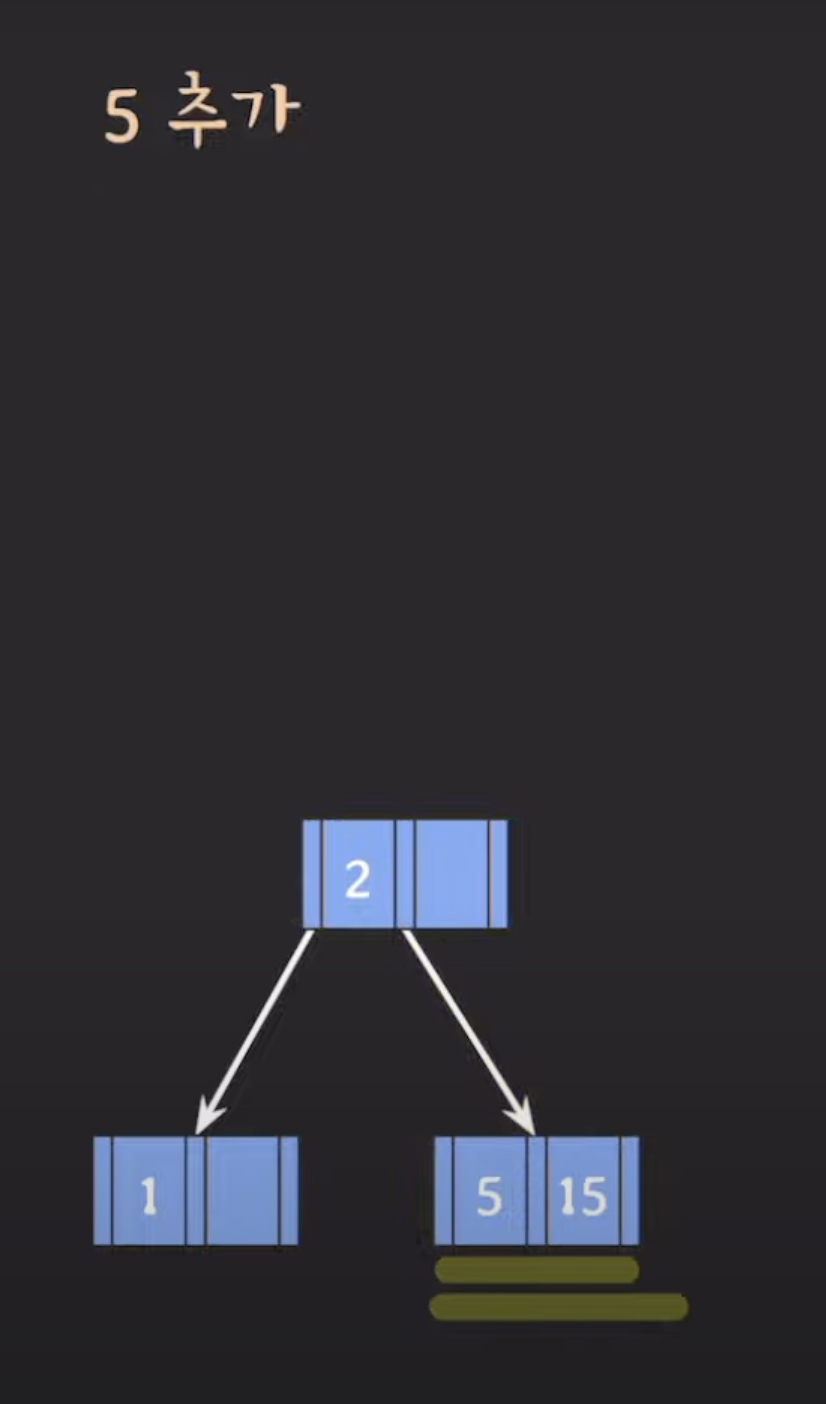
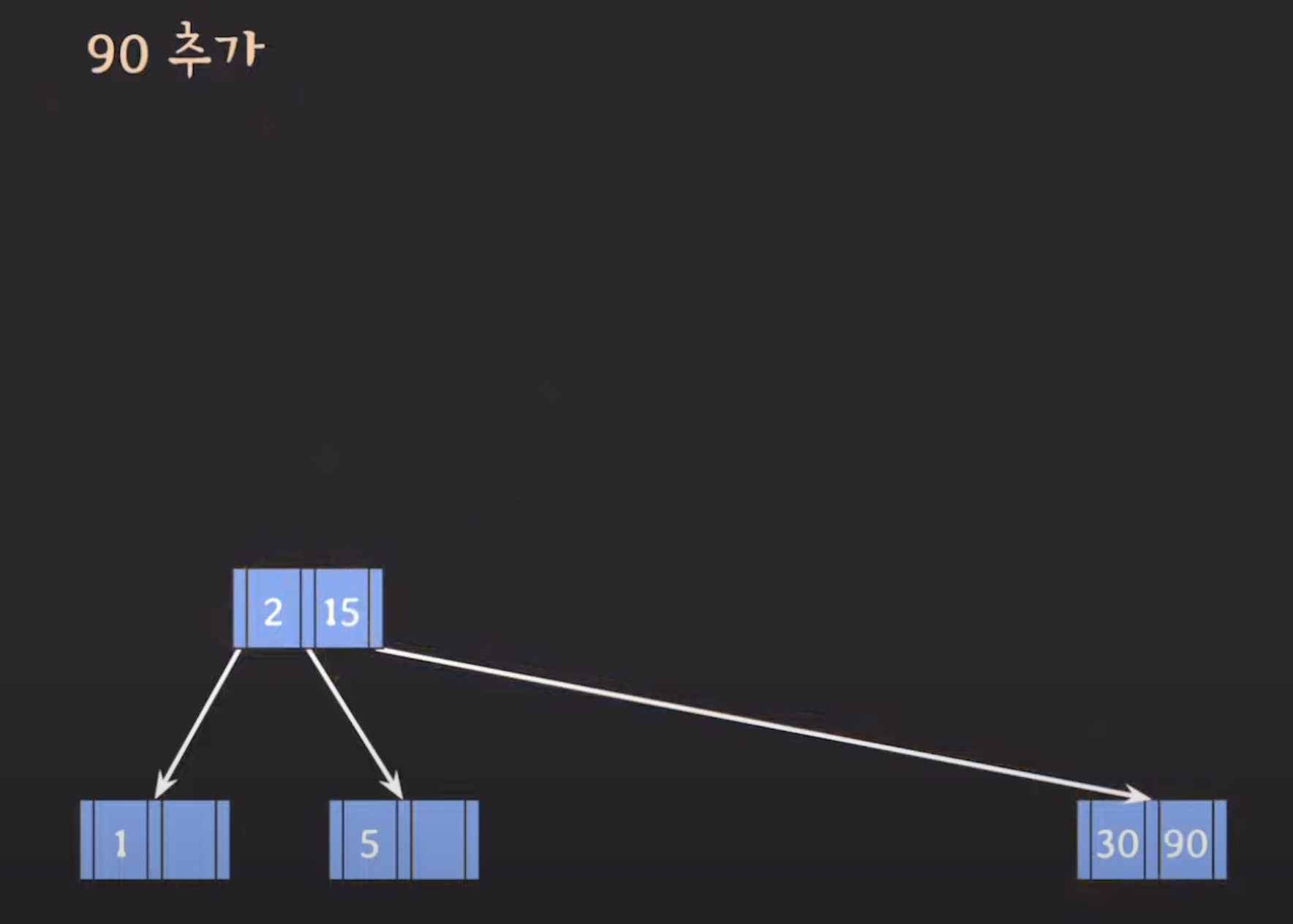
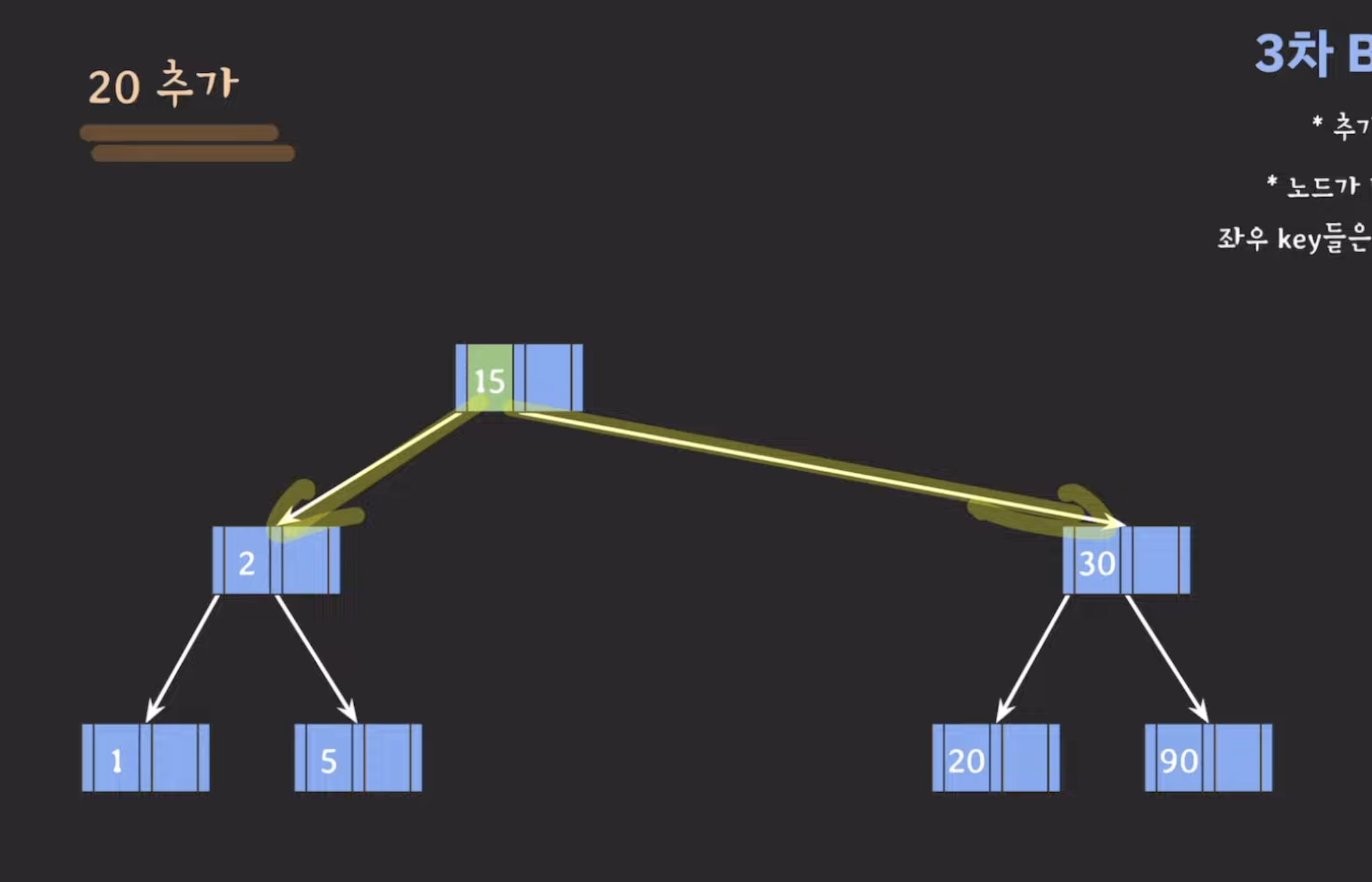
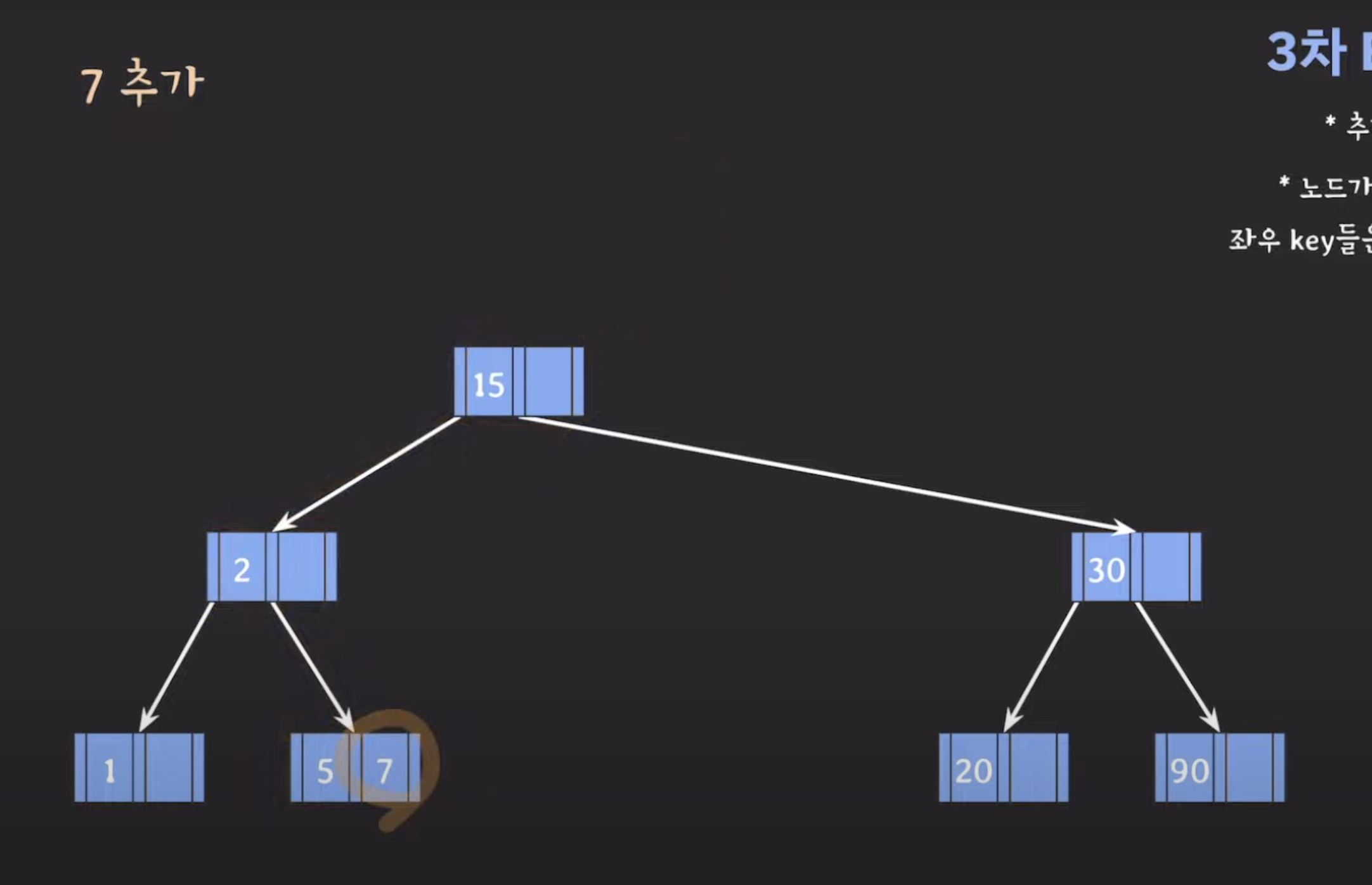
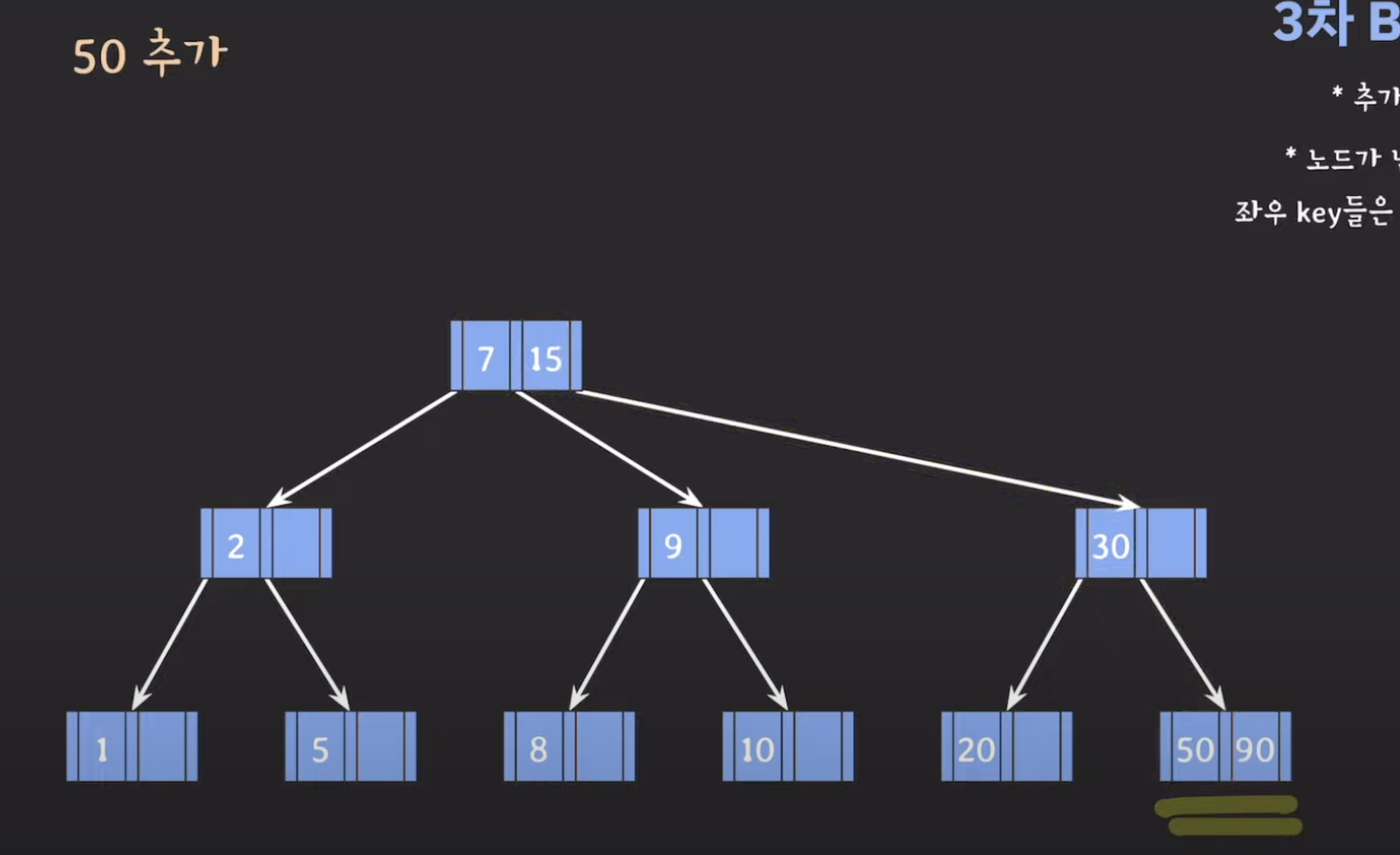
3차 B-Tree 데이터 삽입 예시
B-트리(B-Tree)의 데이터 삽입에 대한 설명을 기반으로 데이터를 삽입하는 예시를 더 자세히 설명해보겠습니다. 먼저, 3차 B-트리의 각 노드의 최대 키(key) 수는 두 개입니다. 이는 각 노드가 최대 두 개의 키를 가질 수 있음을 의미합니다.