52강
문제

내생각
난 이 문제를 풀지 못하였다. 답은 나오지만 1s TimeLimit를 해결하지 못하였다. 이 문제를 풀려고 할 때, 먼저 생각한 것은 코드를 통해서 소인수를 하는 방법이었다. 소인수의 방법은 어떤수 n을 k라는 수로 나누었을 때 나머지의 값이 0이 나온다면 그 값은 소인수의 부분이 된다. 그 후에 n을 k로 나눈 값을 다시 n으로 두고 위의 방식을 반복한다. 만약에 0이 아닌 경우에는 k의 값을 k+1로 변경해준다. 이렇게 while문을 통해서 풀게되면 입력예제의 1500과 같이 결과가 큰 값의 경우 O(n) 이라 할지라도, 연산에 오랜 시간이 걸리게 된다. 사실 이부분은 이미 알고 있었다. 하지만 이 문제를 어떻게 해결해야 할 지를 몰랐다. 몇몇개 생각한 것은 첫번째로 최소값을 나열 할때 해당 값을 2,3,5에 대한 곱으로 나타날때 2,3,5의 지수에 규칙성이 있지 않을까 생각을 했다. 하지만 그 부분은 맞지 않았다. 그리고 그다음 생각한 것이 정답과 비슷한 방법이었는데, 어떤 수에 대해서 2와 3과 5를 각각 곱해서 그 값의 최소값을 구해서 나열하는 방식이었다. 하지만 이 방식의 경우 최소값을 구한 후, 그 다음에 처리를 하는 방법에 대해서 생각을 하지 못하였다.
풀이
이 문제의 경우 pointer의 개념이 들어간다. 여기서 말하는 pointer는 C에서 사용하는 포인터가 아니라 배열의 특정 index 값을 기억하는 변수이다. 일차원 배열에 2,3,5의 곱으로 나타낼 수 있는 수를 나열한다고 할 때 제일 먼저 index=0의 값을 1로 초기화를 한다. 그리고 ptr1, ptr2, ptr3 총 세개의 int형 변수 포인터를 두어 0으로 모두 초기화 한다. 여기서 각각의 포인터의 역할은 2,3,5 각각과 곱하도록 하는 수를 기억하기 위해 존재한다. 이렇게 해주는 이유는 현재 배열에는 2,3,5의 곱으로 나타낼 수 있는 모든 수를 오름차순으로 정렬하여 저장하고 있다. 그렇기 때문에 즉 해당 배열에 있는 모든 값들에 대해서 2,3 또는 5를 곱하게 되면 2,3,5의 곱으로 나타낼 수 있는 모든 수를 구할 수 있기 때문이다.
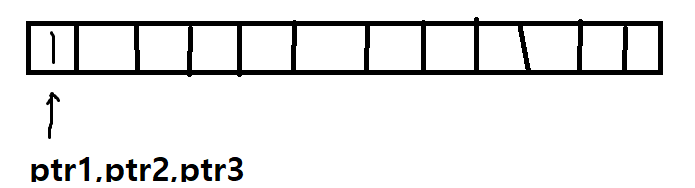
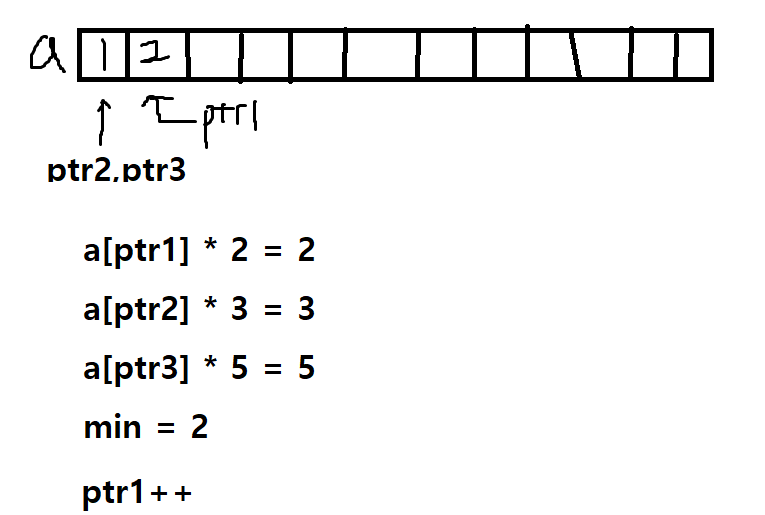
다음 상황은 이와 같은 사진의 상황이 된다. a배열에 ptr을 index값으로 접근하여 해당 값과 각각 2,3,5를 곱하고 그 값들의 최소값을 구하여 a의 채워지지 않은 다음 인덱스에 값을 추가한다. 그 이후 a[ptr] * K = min 값들에 대하여 모두 ptr의 값을 ++ 해준다. 여기서 고려해야 하는 점이 min값을 갖는 ptr이 여러개 있을 수 있다는 것이다. 배열에는 중복된 수를 저장하지 않기 때문에 같은 min값을 가지고 있는 ptr은 모두 ++ 해주어야 하는 것을 기억해야한다.
이 문제를 풀면서 느낀점은 전에 계산한 값들을 배열에 저장하고 그 값들을 이용하여 원하는 값을 도출해내는 것이 중요하다는 것을 알았고, 소인수분해 문제가 나오면 ptr의 개념을 한 번 생각해보자는 점이었다.
